空位及氮掺杂二维ZnO单层材料性质:第一性原理计算与分子轨道分析*
2019-12-24黄炳铨周铁戈吴道雄张召富李百奎
黄炳铨 周铁戈 吴道雄 张召富 李百奎†
1) (深圳大学物理与光电工程学院, 深圳 518060)
2) (南开大学电子信息与光学工程学院, 天津 300350)
3) (中国科学技术大学, 合肥微尺度物质科学国家研究中心, 合肥 230026)
4) (剑桥大学工程系, 剑桥 CB2 1PZ)
采用基于密度泛函理论的第一性原理计算方法, 系统地研究了带缺陷的二维类石墨烯结构的ZnO(graphene like-ZnO, g-ZnO)的几何结构、电子结构、磁性性质和吸收光谱性质.研究的缺陷类型包括锌原子空位(VZn_g-ZnO)、氧原子空位(VO_g-ZnO)、氮原子取代氧原子(NO_g-ZnO)和表面吸附氮原子(N@g-ZnO).研究发现:NO_g-ZnO体系和N@g-ZnO体系形变较小, 而空位体系会引入较大的形变; g-ZnO本身无磁矩, 引入Zn空位后, VZn_g-ZnO体系总磁矩为2.00 µB; VO_g-ZnO体系无磁矩, 但N掺杂后的NO_g-ZnO体系和氮吸附的N@g-ZnO体系的总磁矩分别为1.00 µB和3.00 µB.利用掺杂体系的局域对称性和分子轨道理论分析了杂质能级和磁矩的产生原因, 并且通过分析光吸收曲线得知, 引入空位缺陷或者N原子掺杂, 可以有效增强g-ZnO单层材料的光吸收性能.研究结果对系统地理解g-ZnO及其缺陷模型的性质有重要意义, 可以为发展基于g-ZnO的纳米电子器件和光催化应用提供理论参考.
1 引 言
自从2004年Novoselov等[1]成功制备石墨烯(graphene)以来, 石墨烯凭借其优良的性质[2,3],在各个领域大放异彩.类石墨烯结构的ZnO(graphene like ZnO, g-ZnO)[4]、六方氮化硼 (h-BN)[5,6]、二硫化钼(MoS2)[7,8]等二维纳米材料因其独特的二维结构、大的比表体积等特点, 具有优良的光学、电学、热学性能, 在自旋电子学、催化、纳米电子学等领域有重要的研究价值和巨大的应用潜能[9-11].
2004年, Claeyssens等[12]利用密度泛函理论预测典型Ⅱ-Ⅵ族氧化物g-ZnO可以稳定存在.2007年, Tusche等[13]通过实验验证了当ZnO层数减少至三、四层时, ZnO由纤锌矿结构向类石墨烯蜂窝状结构转变, 成为二维层状g-ZnO.利用第一性原理, 研究人员已对g-ZnO的电子结构、磁性、力学等性质做了进一步的研究[14-16].Guo等[17]用第一性原理计算方法, 研究了非金属元素C,B等取代O原子体系的几何结构和磁性性质.N和O是相邻的元素.如果在制备g-ZnO或后续测试的过程中以氮气作为保护气体, 会不可避免地引入N原子掺杂, 从而引起体系的电子能带结构、磁性和光学等性质的改变, 所以研究N掺杂g-ZnO性质具有重要意义.虽然纤锌矿结构的ZnO的性质和应用已有较多报道[18,19], 其缺陷掺杂方面的理论工作也有报道[20-24], 但是目前系统研究g-ZnO单层材料的空位缺陷以及N原子掺杂(包括取代和吸附)方面的工作尚未有报道.这些工作对进一步研究g-ZnO的物理性质和发展其应用十分必要.特别地, 引入吸附或者掺杂原子是一种调控单层二维材料的几何结构、磁性性质、电子自旋、光吸收等物理特性的有效手段[6,25-28].
本文采用基于密度泛函理论的第一性原理计算方法[29], 对二维g-ZnO具有锌原子空位(VZn_g-ZnO)、氧原子空位(VO_g-ZnO)、氮原子取代氧原子(NO_g-ZnO)、氮原子吸附(N@g-ZnO)的超胞体系的几何结构、电子结构、磁性性质和吸收光谱展开研究, 通过杂质原子的局域对称性, 结合分子轨道理论, 分析了杂质能级和磁性的产生原因.作为对比, 本文也给出了理想情况下无缺陷的二维ZnO (g-ZnO)单层的计算结果.
2 理论模型与计算方法
研究中采用基于密度泛函理论的第一性原理计算软件包 Viennaabinitiosimulation package(VASP)[30]进行计算, 几何结构优化采用广义梯度近似 (GGA)中的 Perdew-Burke-Ernzerhof交换关联泛函[31], 为了避免经典半局域化GGA泛函引入的禁带宽度低估这一缺点, 在电子结构计算中采用杂化泛函Heyd-Scuseria-Ernzerhof (HSE06)[32].计算中, 赝势选用投影缀加平面波[33], 平面波截断动能测试范围为 300—600 eV, 每隔 50 eV 测试一次, 测试后的截 断能最终选定为 500 eV.采用VASPKIT软件包对计算的数据进行后处理[34].
g-ZnO的原胞包含1个Zn原子和1个O原子, 本文先对1 × 1的g-ZnO原胞进行晶格常数优化(固定真空厚度, 仅在XY方向自由弛豫原子)以及研究其电子结构.基于优化后的晶格常数扩建超胞, 对于空位与掺杂g-ZnO超胞体系, 几何优化时固定超胞晶格常数, 仅对原子的位置进行结构优化.为了消除缺陷中心原子与相邻原胞的相互影响, 对 g-ZnO 进行扩胞, 采用 5 × 5 的 g-ZnO超胞进行Zn, O空位和N掺杂研究.经扩胞后, 未掺杂的g-ZnO由25个Zn原子和25个O原子组成.同时为了避免因为周期性边界条件引起的镜像结构之间的相互影响, 在Z轴方向加15 Å厚度的真空层.计算由两部分构成, 首先对体系进行几何结构优化, 然后对得到的稳定的几何结构进行电子结构、磁性和吸收光谱计算分析.在几何优化中采用以Γ点为中心的 3 × 3 × 1 的k点网络, 收敛标准为每个原子的力小于0.01 eV/Å.几何优化和静态计算的电子弛豫精度均设为10—5eV.
3 计算结果与讨论
3.1 晶体结构与结合能
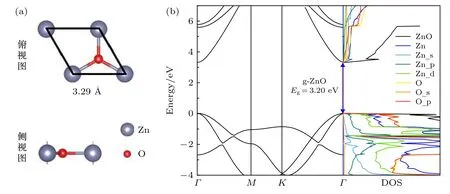
图1 理想g-ZnO的(a)晶体结构以及(b)能带和态密度, 其中g-ZnO价带顶对齐到0 eVFig.1.(a) Atomic structures, (b) band structure and density of states (DOS) of the g-ZnO primitive unit cell.The valence band maximum of g-ZnO is referred to 0 eV.
g-ZnO单层是二维的六方结构, 其单胞如图1所示, 其Zn原子与O原子处于同一个原子层, 有别于立体的ZnO的六方纤锌矿和立方闪锌矿构型.经优化后的理想的g-ZnO的晶格常数a=3.29 Å, Zn—O 键的键长为 1.90 Å, 与之前的实验和理论数据相吻合[4,13,14].经过杂化泛函计算得到的g-ZnO的能带和态密度如图1(b)所示.g-ZnO的禁带宽度为3.20 eV, 其价带顶和导带底均在Γ处, 为直接带隙半导体, 与其他理论计算值[35,36]相一致.由图1(b)态密度图中的总态密度(total density of states, TDOS)和分波态密度 (partial density of states, PDOS)曲线可知, 价带主要由Zn原子的3d轨道和O原子的2p轨道组成, 其中O-2p轨道的贡献更加大, 而导带主要在Zn的4 s轨道和O原子的2s轨道的作用下产生.
如前所述, VZn_g-ZnO 体系为 5 × 5 的 g-ZnO超胞缺失一个 Zn原子, VO_g-ZnO体系为 5 × 5的g-ZnO超胞缺失一个O原子, NO_g-ZnO体系为g-ZnO超胞中的一个O原子被N取代, N@g-ZnO体系为一个N原子吸附在5 × 5的g-ZnO超胞上.图2展示了这些超胞优化后的几何结构, 其中图2(d)—(f)为N吸附g-ZnO的三种可能构型.如图2(a)所示, 在VZn_g-ZnO体系中, Zn空位周围的3个O原子都远离Zn空位中心, O1-O2, O1-O3, O2-O3 的距离均为 3.64 Å, 明显大于理想 g-ZnO 中 O—O 键的键长 3.29 Å, 分别以 O1, O2,O3为顶点, 与最近邻的两Zn原子的夹角均由120.00°变为 133.79°.优化后的原子坐标变化趋势与我们之前的研究结论相吻合[26-28].如图2(b)所示, 在 VO-g_ZnO体系中, O空位周围的 3个Zn原子都向O空位中心靠拢, Zn1-Zn2, Zn1-Zn3,Zn2-Zn3的距离均为 2.64 Å, 明显小于 g-ZnO 的晶格常数a= 3.29 Å, 分别以 Zn1, Zn2, Zn3 为顶点, 与最近邻的两O原子的夹角均由120.00°变为104.98°.如 图2(c)所 示 , 在 NO_g-ZnO体 系 中 ,N原子取代O原子后, N原子与最近邻的3个Zn原子的键长均为1.92 Å, 与理想的g-ZnO体系的 Zn—O键的键长 1.90 Å 差别可以忽略, 杂质N原子离g-ZnO平面0.07 Å, 该体系发生的形变较小.原因可能为N与O为相邻的元素, 原子半径差异较小, 均可以产生 sp2杂化.对于 NO_g-ZnO体系的结合能的计算公式为
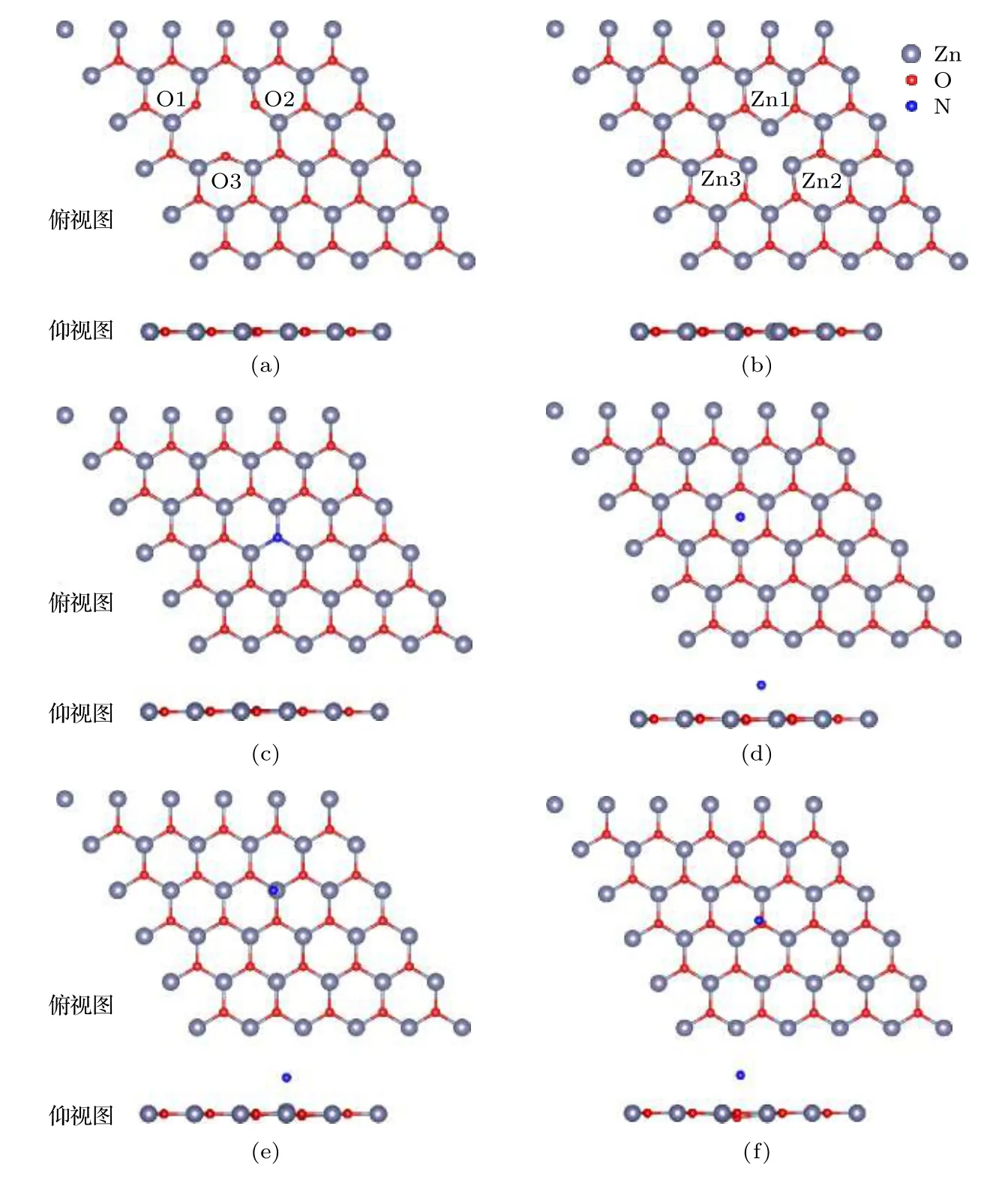
图2 空位及掺杂超胞体系的几何结构示意图 (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N 原子吸附在六元环中心上方; (e) N 原子吸附在 Zn 原子上方; (f) N 原子吸附在 O 原子上方Fig.2.Atomic structures of the g-ZnO supercells:(a) Ideal g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N atom at hollow site; (e) N atom on top of Zn atom; (f) N atom on top of O atom.
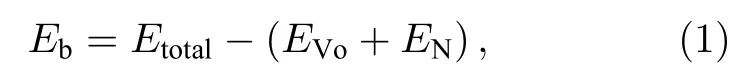
其中Eb为结合能, 反映掺杂后体系的稳定性,Eb越小体系越稳定;Etotal为优化后的体系的总能量;EVo为 VO_g-ZnO 体系的总能量;EN为独立的N原子的能量.NO_g-ZnO体系的结合能Eb为—4.12 eV, 为负值, 说明该掺杂体系比较稳定.
对于N@g-ZnO体系, 根据高度对称性研究了三种吸附模型:1) N原子吸附在g-ZnO的六元环中心上方; 2) N原子吸附在g-ZnO单层的Zn原子上方; 3) N原子吸附在g-ZnO单层的O原子上方.具体结果分别如图2(d)—(f)所示.计算表明,上面的三种结构, N原子距离g-ZnO平面的距离分别为 2.12, 2.25, 2.31 Å.对于 N 吸附体系的结合能计算公式为
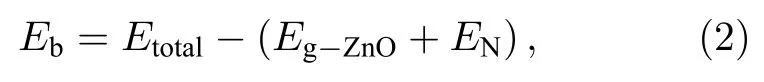
其中Eb为结合能,Etotal为优化后的体系的总能量,Eg-ZnO为理想 g-ZnO体系的总能量,EN为独立的N原子的能量.上述三种结构的结合能Eb分别为:—0.25, —0.19, —0.15 eV.结合能均为负值, 表示可以稳定吸附在g-ZnO上.选取这三种吸附结构中结合能Eb最小即最稳定的结构(N吸附在g-ZnO六元环中心上方)做进一步研究.以下N@g-ZnO体系中均为N原子吸附在g-ZnO六元环中心上方体系的性质.N掺杂 g-ZnO单层体系NO_g-ZnO和N@g-ZnO的5 × 5的超胞模型优化后有关晶格参数以及结合能Eb如表1所列.
表1中的hN为掺杂N原子(取代模型或者吸附模型)与g-ZnO平面的距离,hZn和hO分别为和掺杂N原子最近邻的Zn, O原子与g-ZnO平面的距离, 反映掺杂后体系的形变程度.dZn_N为掺杂N原子与最近邻的Zn原子的键长,dO_N为掺杂N原子与最近邻的O原子的键长, 反映掺杂N原子与体系的Zn, O原子的相互作用.从表1可以看出, 无论取代模型还是吸附模型, N原子掺杂对g-ZnO本身的结构性质的影响均较小.
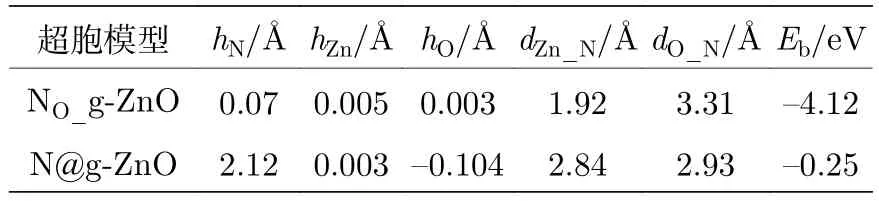
表1 N掺杂g-ZnO单层的结构参数和结合能Table 1.Structure parameters and binding energy of N-doped g-ZnO monolayer.
3.2 电子结构
利用杂化泛函计算得到的超胞体系的总态密度以及分波态密度如图3所示, 图中0 eV为g-ZnO价带顶的位置.
理想的g-ZnO体系是无磁性的.当引入Zn空位后, VZn_g-ZnO体系在价带以上0.72和1.21 eV分别出现两个自旋向下的杂质能级(图3(a)), 其中在价带顶0.72 eV处自旋向下的杂质能级位于费米能级以下, 氮原子与其对应的自旋向上的能级因为能级分裂的原因, 出现在价带顶附近, 由价带附近的自旋向上和自旋向下的能级不是严格对称说明了这一点.PDOS结果表明, 该杂质能级主要是由氧原子贡献, 来源于与空位Zn原子近邻的三个氧原子.当引入O空位后, VO_g-ZnO体系没有磁性, 磁矩为零, 该体系的态密度上下自旋对称(图3(b)), 并且态密度图中VO_g-ZnO体系的禁带中没有出现杂质能级.N掺杂体系禁带中出现明显的杂质能级, 其中N替位O体系(图3(c))的杂质能级靠近导带, 在价带顶以上2.41 eV处出现自旋向下的杂质能级, PDOS表明杂质能级主要是N原子贡献.吸附体系即N@g-ZnO体系(图3(d))的杂质能级靠近导带, 在价带顶以上3.01 eV处出现杂质能级, 该杂质能级则是主要由吸附的N原子贡献.后面将结合自旋密度和分子轨道理论对上述结果进行更加详细的解释.
g-ZnO的Zn空位、O空位、N掺杂的能带结构如图4所示, 同本征g-ZnO一样, 四种缺陷体系均为直接带隙半导体.其中VZn_g-ZnO的杂质能级由3条自旋向下的轨道构成, 其中在价带顶以上 1.21 eV处的 2条杂质能级轨道简并.NO_g-ZnO的杂质能级由1条自旋向下的轨道构成.N@g-ZnO的杂质能级由靠近导带的3条简并杂质能级轨道构成, 其中1条轨道与另外两条能量稍高且完全简并重合的轨道发生微小的分裂.后面将结合自旋密度和分子轨道理论对上述结果进行更加详细的解释.

图3 总态密度和分波态密度 (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO; 其中 g-ZnO 的价带顶对齐到 0 eVFig.3.Total density of states and partial density of states:(a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO.The valence band maximum of g-ZnO is referred to 0 eV.
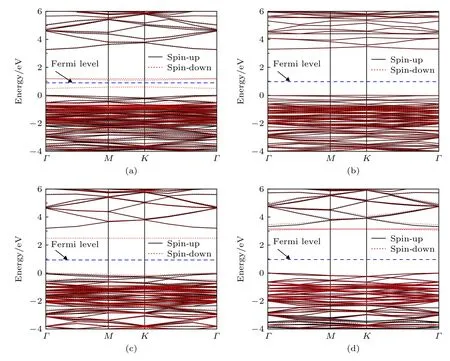
图4 能带结构 (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO; 其中 g-ZnO 的价带顶对齐到 0 eVFig.4.Band structure of (a) VZn_g-ZnO; (b) VO_g-ZnO; (c) NO_g-ZnO; (d) N@g-ZnO.The valence band maximum of g-ZnO is referred to 0 eV.
3.3 磁性性质
3.3.1 体系的磁矩及分子轨道分析
表2列出了空位体系和N掺杂g-ZnO单层超胞的总磁矩 (Mtot), 以及掺杂 N原子 (MN)、与N原子最近邻的Zn原子(MZn)、与N原子最近邻的O原子(MO)的局域磁矩.
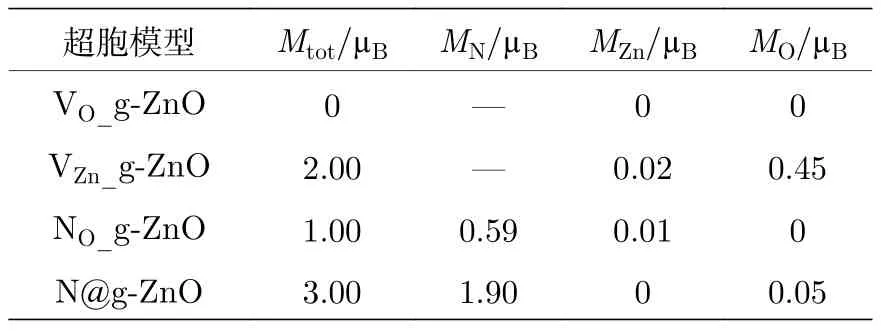
表2 N 掺杂 g-ZnO 单层的磁矩Table 2.Magnetic moment of N-doped g-ZnO monolayer.
理想的g-ZnO和VO_g-ZnO体系中Zn原子和O原子的价电子均成键, 没有未成对的电子, 所以均没有磁性, 磁矩为零.这与图3中这两个体系的自旋态密度图上下对称相一致.下面用分子轨道理论, 结合缺陷体系的局域对称性, 讨论另外三个有磁性的体系的磁性成因.
VZn_g-ZnO 体系的总磁矩为 2.00 µB, 与 Zn 空位相邻的3个O原子的局域磁矩依次为0.44 µB,0.45 µB, 0.46 µB.当 g-ZnO 体系缺少一个 Zn 原子时, 缺陷呈现D3h对称性, 缺陷周围3个氧原子有3个σ键, 而且体系缺少2个价电子(一个Zn原子有2个价电子).3个σ键在D3h对称性下的分裂成 E'(二重简并)和(单重简并)两个不可约表示, 并且位于费米能级以下, 如图5(a)所示.由于缺少2个价电子, E'能级(最多占据4个电子)只存在2个电子, 这2个电子以自旋向上的形式占据 E'能级, 所以体系的总磁矩为 2.00 µB.态密度曲线中的杂质能级是由未被电子填充的自旋向下的E'能级产生, 杂质能级发生轻微的分裂是由于对称性并非严格的D3h.
由表2的数据可知, N替位O的g-ZnO单层的总磁矩为 1.00 µB, N 原子的局域磁矩为 0.59 µB,与之前的报道一致[17].由于O是—2价, N是—3价,所以N取代氧时, 体系缺少一个价电子.优化后的体系具有D3h的局域对称性, N原子的 px, py和pz三个轨道在D3h对称性下的分裂成E'(二重简并, px和 py)和(单重简并, pz)两个不可约表示, 如图5(b) 所示.A2''能级上缺少一个自旋向下的电子, 因而体系的总磁矩为 1.00 µB.由于 A2''能级主要源自pz轨道, 可以在图6(c)的自旋密度图中明显看出其自旋密度具有pz轨道的形状.
当N原子吸附在g-ZnO的六元环中心上方时, 其总磁矩为 3.00 µB, 其局域磁矩也是主要分布在吸附的N原子上, N原子的局域磁矩为1.90 µB.N@g-ZnO体系具有C3v局域对称性.对于孤立N原子px, py和pz三个轨道彼此简并, 吸附后在C3v晶体场影响下, 分裂为 A1(pz)和 E (px, py)两个不可约表示, 其中A1为一重简并, E为二重简并, 能带结构图(图4(d))验证了这一点, 分子轨道如图5(c)所示.在态密度曲线上可以明显看出A1和E能级的存在.由于分裂较小, N原子的3个p电子以自旋向上的方式分别填充在A1和E 能级, 所以体系总磁矩为 3.00 µB.px, py和 pz三个轨道自旋向上都被填充满, 所以图6(d)的自旋密度呈现球对称性.
3.3.2 自旋密度
自旋密度图可以更加直观地分析体系的磁矩分布情况.图6给出了四种超胞体系的自旋密度.
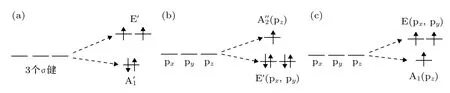
图5 分子轨道 (a) VZn_g-ZnO 体系, O 能级劈裂及电子填充示意图; (b) NO_g-ZnO 体系, p 轨道分裂及电子填充示意图;(c) N@g-ZnO体系, p轨道分裂及电子填充示意图Fig.5.Molecular orbital diagrams:(a) VZn_g-ZnO supercell, O energy level splitting and electron filling; (b) NO_g-ZnO supercell,p-orbital splitting and electron filling; (c) N@g-ZnO supercell, p-orbital splitting and electron filling.
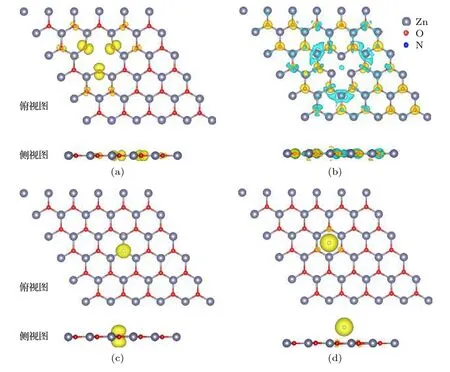
图6 自旋密度图, 其中青色区域是自旋向上, 黄色区域是自旋向下 (a) VZn_g-ZnO 体系的自旋密度; (b) VO_g-ZnO 体系的自旋密度; (c) NO_g-ZnO 体系的自旋密度; (d) N@g-ZnO 体系的自旋密度Fig.6.Spin density of (a) VZn_g-ZnO, (b) VO_g-ZnO, (c) NO_g-ZnO, and (d) N@g-ZnO supercells, respectively.Cyan is spin up and yellow is spin down.
从图6可以清楚地看出, 在VZn_g-ZnO体系中, 如图6(a), 磁矩主要分布在空位附近的3个O原子上, 与表2的数据相一致.在VO_g-ZnO的自旋密度可知, 该体系上下旋基本对称, 总磁矩为零.两种N掺杂的g-ZnO体系的局域磁矩主要分布在掺杂 N原子上 (图6(c)和图6(d)), 与掺杂N原子相邻的Zn原子和O原子只有少量磁矩分布, 这与表2的数据相一致.并且在NO_g-ZnO体系中, N的自旋密度呈哑铃状(图6(c)), 与上述分析能级来源于 N原子的 pz轨道相一致.在N@g-ZnO体系中(图6(d)), 吸附的N原子的自旋密度呈球状进一步验证轨道分析px, py和pz三个轨道自旋向上都被填充满.
3.4 光学性质
g-ZnO是良好的光催化剂, 在光解水领域研究比较广泛, 常与 MoS2, C3N4, BP 等二维材料结合成异质结, 实现光生载流子的分离, 分解水产生氢气和氧气[36-38].在此给出所研究的五种体系的光吸收光谱, 如图7所示.理想g-ZnO单层的吸收曲线与文献[39]报道相吻合, 从吸收曲线上升沿反向延长线可以看出其禁带宽度近似为3.2 eV, 与图1(b)的能带计算相吻合.
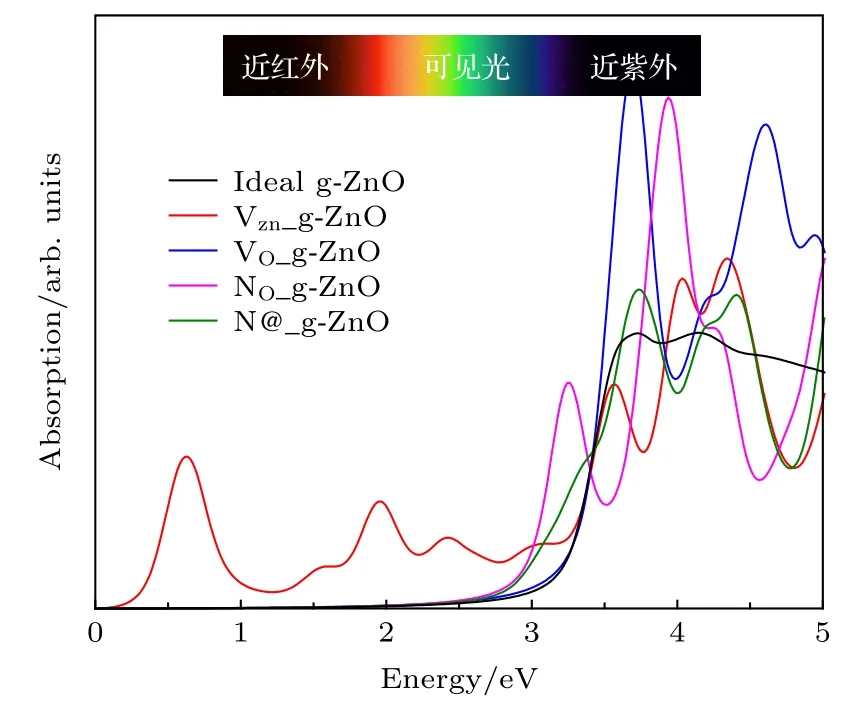
图7 理想g-ZnO及具有空位、掺杂的超胞体系的光学吸收谱Fig.7.Optical absorption spectra of ideal g-ZnO and the defective supercell systems.
研究的四种缺陷体系中, O空位体系因禁带中未出现杂质能级, 其吸收曲线与理想g-ZnO几乎重合.而两种N掺杂体系因为在导带底附近出现了较浅的杂质能级, 导致其吸收曲线上升沿向低能方向移动.其中NO_g-ZnO的吸收曲线在3.1 eV出现明显的吸收峰, 起源于N掺杂引入的杂质能级跟价带顶之间的光学跃迁.对于Zn空位体系,从图3态密度和图4能带图可知, 该体系在价带顶以上1 eV附近存在空位引起的杂质能级, 这些杂质能级与价带顶之间的光学跃迁导致VZn_g-ZnO在近红外区存在吸收峰.由于计算的能带图中能级为体系基态的Kohn-Sham能级位置, 而吸收曲线反映光学跃迁性质, 因为存在斯托克斯位移, 吸收峰的位置与能带图中杂质能级位置并不完全相等.计算得到的吸收曲线表明, 通过引入空位缺陷或者N原子掺杂, 可以有效增强g-ZnO单层材料的光吸收性能, 这对实现基于g-ZnO的光催化反应等应用领域有重要参考意义.
4 结 论
本文采用基于密度泛函理论的第一性原理计算方法, 系统地对理想g-ZnO单层, 以及含有空位和 N 掺杂即 VZn_g-ZnO, VO_g-ZnO, NO_g-ZnO,N@g-ZnO四种缺陷体系进行几何结构、电子结构、磁性性质和光吸收光谱进行了研究.研究结果表明:两种空位体系中体系形变均较大, VZn_g-ZnO 体系的总磁矩为 2.00 µB, VO_g-ZnO 体系无磁矩; 而N掺杂体系形变则较小, 其中NO_g-ZnO的N原子p轨道分裂成E'和两个不可约表示,使得总磁矩为1.00 µB; N@g-ZnO体系中N原子最稳定吸附位置为六元环中心上方, 该N原子的3个p电子以自旋向上的方式填充分子轨道, 使得总磁矩为 3.00 µB.基于分子轨道理论, 较好地解释了杂质能级和磁矩产生的原因.在光学性质角度,研究发现通过空位或者掺杂可以有效调控g-ZnO的光吸收性能.这些结论对深入理解g-ZnO单层其缺陷体系性质有重要参考价值, 可为进一步研究基于g-ZnO的纳米电子器件等应用领域提供理论参考.
