多晶石墨烯纳米带热电性能的理论研究*

许易 许小言 张薇 欧阳滔 2)† 唐超2)‡

1) (湘潭大学物理与光电工程学院, 湘潭 411105)

2) (湘潭大学, 微纳能源材料与器件湖南省重点实验室, 湘潭 411105)

热电材料能够将废热能直接转换成电能, 近年来受到了科技工作者们的广泛关注.本文采用非平衡格林函数方法系统地研究了晶界对石墨烯纳米带热电性能的调控作用.研究结果表明：晶界能有效地提高石墨烯纳米带的塞贝克系数, 同时可以极大地抑制其热导(包含电子和声子部分).基于这两个积极的效应, 多晶石墨烯纳米带的热电转换性能得到了显著的增强.在室温下, 多晶石墨烯纳米带的热电品质因子约为0.3, 较完美石墨烯纳米带(约为0.05)提升了6倍左右.并且发现晶界的数量和系统的长度还能进一步提升多晶石墨烯纳米带的热电性能, 但系统的宽度对其影响有限.这些结果表明, 多晶结构可以显著提升石墨烯纳米带的热电转换效率.这将为设计和制备基于石墨烯纳米带的热电器件提供新的途径.

1 引 言

热电材料作为能将热能和电能进行相互转换的一种功能材料, 其应用近年来受到了人们广泛的关注, 其热电转换效率可以采用热电品质因子ZT=σS2T/k来衡量, 其中S为塞贝克系数,σ为电子电导,k为热导(包含电子贡献部分ke和声子贡献部分kp).由于电子和声子输运之间强烈的耦合性,因此传统的块体材料热电品质因子普遍较为低下[1].然而, 近年来的研究表明, 由于量子限域效应的影响, 低维纳米材料显现出比传统块体材料更高的热电转换效率[2-6].因此, 寻找具有优异热电转换性能的纳米材料或改良现有纳米材料的热电性能已成为目前热电研究领域的一大热点.

自从2004年发现石墨烯以来, 石墨烯及其衍生纳米结构引起了人们广泛的兴趣.因为石墨烯具有独特的几何结构, 其纳米结构具有许多优异的物理属性[7-9].例如：良好的机械力学性能[10]、较高的热稳定性[11], 以及出色的光学特性[7,12].更为有趣的是, 石墨烯具有超高的载流子迁移率, 其在室温下可达 200000 cm2/(V·s)[13].Dragoma 等[14]发现石墨烯的塞贝克系数高达30 mV/K, 是目前已知材料中最高的.这预示着石墨烯将有可能成为一种理想的热电材料.然而, 研究发现石墨烯的热导高达 3000 W/mK (悬浮样品)[15,16], 这极大地限制了其在热电领域的广泛应用.近年来, 人们提出了多种方法来有效地减低石墨烯的热导进而提高其热电品质因子, 例如：超晶格[17]、缺陷工程[18,19]、掺杂[20,21].这些手段均能在一定程度上增强石墨烯的热电转换性能, 同时也有效地推动了对石墨烯热电性质研究的发展.不过, 值得注意的是, 实验合成和制备的石墨烯, 由于其生长基底和石墨烯成核晶向的差异性, 往往更容易形成多晶结构[22,23].事实上, 多晶结构是调控材料物理性质的有效途径之一[24-26].先前的分子动力学模拟研究也表明, 多晶石墨烯中的晶界能对声子产生极大的散射效果, 进而极大地降低其热输运性能[27].然而, 迄今为止鲜有研究工作关注到晶界对石墨烯及其衍生纳米结构电子输运性质尤其是热电性质的影响.

本文采用非平衡格林函数方法[28,29]系统地探索了晶界对石墨烯纳米带热电性能的调控作用.研究结果表明, 晶界能有效地增强石墨烯纳米带的热电转换效率.在室温下, 晶界的存在可将完美石墨烯纳米带的热电品质因子提高6倍(从0.05提升至0.3).这主要归因于晶界提高了石墨烯纳米带的塞贝克系数以及有效地抑制了其热导(包含电子和声子部分).还讨论了尺寸效应对多晶石墨烯纳米带热电性能的影响.发现多晶石墨烯纳米带的热电品质因子会随着长度的增加而上升, 随着宽度的增加而逐渐下降.这些结果表明, 多晶结构可以显著提升石墨烯纳米带的热电转换效率.这将为设计和制备基于石墨烯纳米带的热电器件提供新的途径.

2 模型和方法

图1展示的是多晶石墨烯纳米带原子结构模型.整个结构可以分成3个不同的区域：由完美锯齿型石墨烯纳米带构成的左右电(热)极, 以及由多个不同晶向石墨烯片组成的中心区.这里多晶石墨烯纳米带晶界的数量用N来表示, 中心区的长度和宽度分别用L和W来表示.

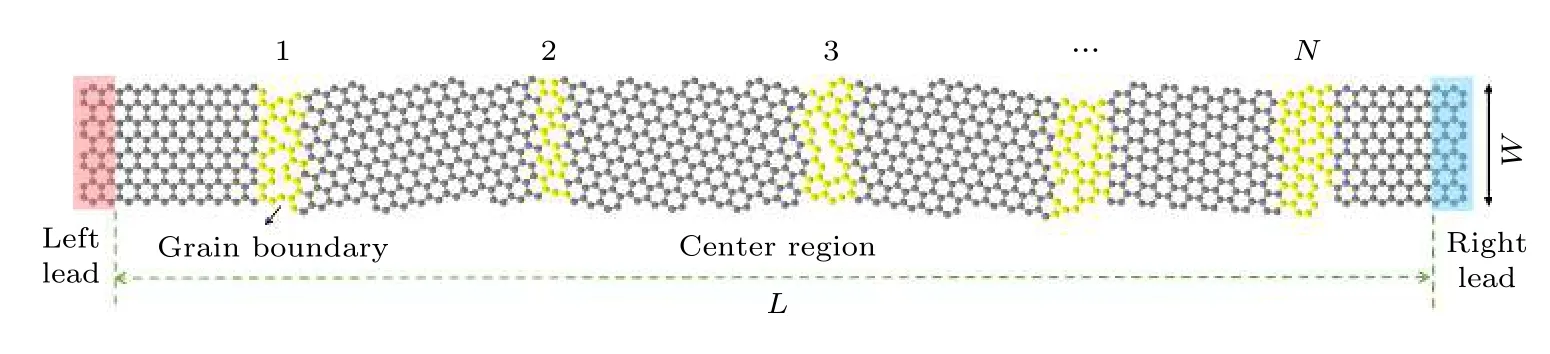
图1 多晶石墨烯纳米带原子结构模型示意图Fig.1.Schematic diagram of polycrystalline graphene nanoribbons.

采用非平衡格林函数方法来计算系统的电子和声子输运性质[28,29].需要指出的是, 由于石墨烯中电声耦合较弱以及较长的电子和声子平均自由程, 因此在计算过程中忽略了电声耦合效应, 并认为电子和声子是独立进行输运的.先前有关石墨烯热电性能的研究均采用类似的处理方法[30,31].对于多晶石墨烯纳米带的电子输运性质部分, 采用紧束缚模型来构造其哈密顿量[32], 该哈密顿量可以表示为

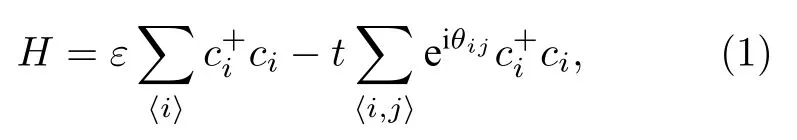
其中ε为格点能并设为0;t为跃迁能, 其值具有距离依赖关系,t=t0exp[-3.37(l/a-1)][33], 其中t0是石墨烯的原始跃迁能,l和a(1.42 Å)分别为碳原子之间的距离和原始石墨烯中最近邻石墨烯的C—C键长.基于(1)式所给出的紧束缚哈密顿量, 电子的推迟格林函数可以写为

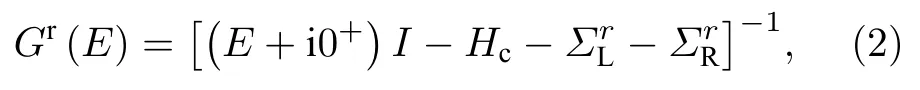
其中E为电子能量;代表半无限长左(右)电极的自能, 其可以通过快速迭代方法进行求解.基于超前格林函数Ga(E)=Gr(E)†和自能可以计算并获得系统的电子透射系数Te(E)[32]：

其中f(E,µ,T) 为费米-狄拉克分布函数,µ是化学势,E是入射电子的能量,T是温度.σ,S和ke可以用以下公式计算：

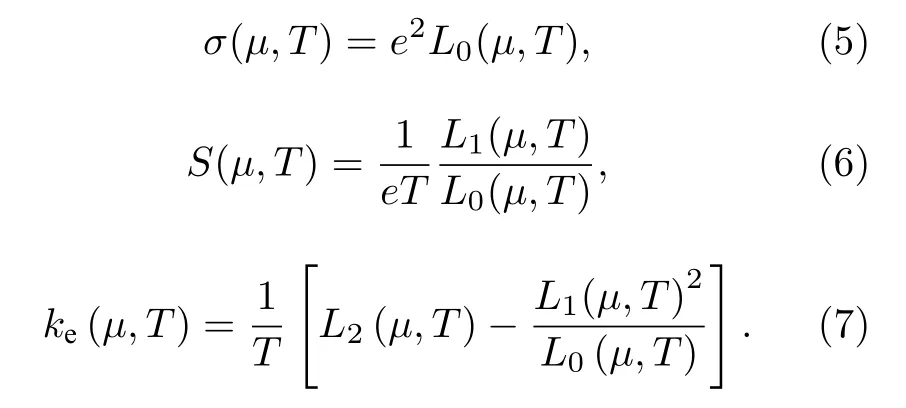
与电子推迟格林函数类似, 声子推迟格林函数可以表示为

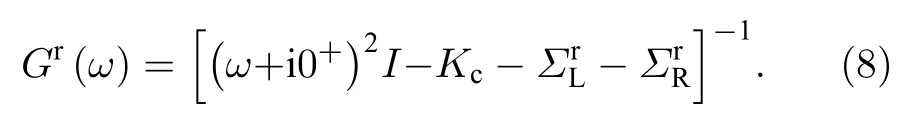
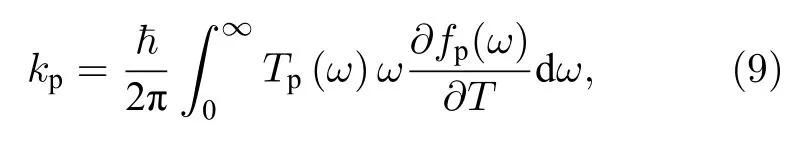
其中fp(ω)为玻色-爱因斯坦分布函数.

此外由声子推迟格林函数还可以得到声子局域态密度：

最后, 基于上述公式多晶石墨烯纳米带中的热电品质因子ZT可以表示为

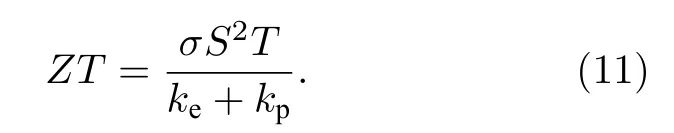
3 结果与讨论

首先研究了晶界对石墨烯纳米带声子输运性质的影响.图2(a)显示了完美石墨烯纳米带和具有不同晶界数的石墨烯纳米带声子热导κph随温度的变化.需要指出的是, 图2(a)中多晶石墨烯纳米带的热导数据为统计平均后的结果.为了获得该结果, 在计算中统计了至少20个不同的多晶石墨烯纳米带样品.从图2(a)可以明显地观察到, 多晶石墨烯纳米带的热导远远低于完美石墨烯纳米带的值, 并且其还会随着晶界数目的增加继续降低.例如：在300 K时, 完美石墨烯的声子热导约为2.5 nW/K, 当系统中存在3个晶界时声子热导率仅为 0.26 nW/K, 而当晶界数目增加到 7 时, 声子热导率进一步下降至0.15 nW/K.为了理解这一现象, 计算了相应的声子透射系数, 如图2(b)所示.对于完美石墨烯纳米带, 可以发现声子透射系数为量子化平台状, 并且其透射系数数值与声子色散关系中的输运通道相对应.而当系统引入晶界后, 输运量子化平台受到破坏, 声子透射系数也急剧下降.这说明声子在通过多晶石墨烯纳米带过程中受到了晶界强烈的散射.另外, 值得一提的是,在多晶石墨烯纳米带中, 低频声子尽管拥有较长的波长, 其仍然遭到了晶界的散射.为了更为直观地展现出声子在多晶石墨烯纳米带中的输运行为,图2(c)—(e)给出了3个典型频率下的声子局域态密度.可以看出, 这3个典型频率的声子均受到了极大的散射, 从而其主要局域在晶界附近没有形成有效的输运通道.也正是因为晶界的散射作用以及声子输运通道的破坏才导致了多晶石墨烯纳米带的热导远低于完美石墨烯纳米带的值.这些研究结果表明, 晶界散射行为对提高石墨烯纳米带的热电性能将发挥积极作用.

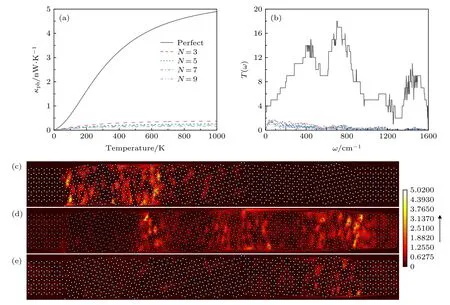
图2 完美石墨烯纳米带和多晶石墨烯纳米带的 (a)声子热导和 (b)声子透射系数 (其中 L = 196.48 Å, W = 17.04Å);(c)(e)多晶石墨烯纳米带 (N = 5)在 3 个典型频率下 (频率分别是 160.68, 585.04, 951.72 Hz)的声子局域态密度Fig.2.Comparison of (a) the phonon conductance, (b) the phonon transmission for perfect graphene nanoribbons and polycrystalline graphene nanoribbons (where L = 196.48 Å, W = 17.04 Å); (c)-(e) the local density of states in polycrystalline graphene (N = 5)at three typical frequency (160.68, 585.04 and 951.72 Hz).

图3(a)给出了完美和多晶石墨烯纳米带的电子透射系数.采用的是键长依赖的紧束缚模型, 因此所获得的电子透射系数要较先前基于最近邻紧束缚模型所得到的结果更为优异和精确.与多晶石墨烯纳米带中的声子情况类似, 晶界同样会破坏电子的输运通道并且对通过多晶结构的电子产生散射作用.因此, 从图3(a)可以看到晶界破坏了完美石墨烯纳米带的电子输运量子化平台, 而且极大地降低了透射系数数值.随着晶界数目的增加, 输运通道进一步受到破坏, 散射作用也进一步增强, 因此多晶石墨烯纳米带的电子透射系数进一步下降.依据 (5)和(7)式, 可以发现电子电导和电子热导均与电子透射系数直接关联.因此, 如图3(b)和图3(c)所示, 电子电导和电子热导同样会随着晶界的引入而急剧下降, 并随着晶界数目的增加而进一步减弱.对于塞贝克系数而言, 其与电子透射系数的偏微分密切关联.透射系数跳变越大, 塞贝克系数也会越大.从图3(d)可以看到完美石墨烯纳米带的塞贝克系数峰位于—1.39, —0.62 和 0.59 eV附近.而对于多晶石墨烯纳米带, 晶界破坏了电子透射系数的量子化平台, 产生了较多的峰谷结构.因此其塞贝克系数峰的分布更为广泛, 并且其最大值也从完美石墨烯纳米带的0.066 mV/K提升至0.20 mV/K (N= 7).塞贝克系数的增强对于石墨烯热电性能的提升发挥着积极的作用.同时分布更为广泛的塞贝克系数峰也方便了实验方面操作的实现.

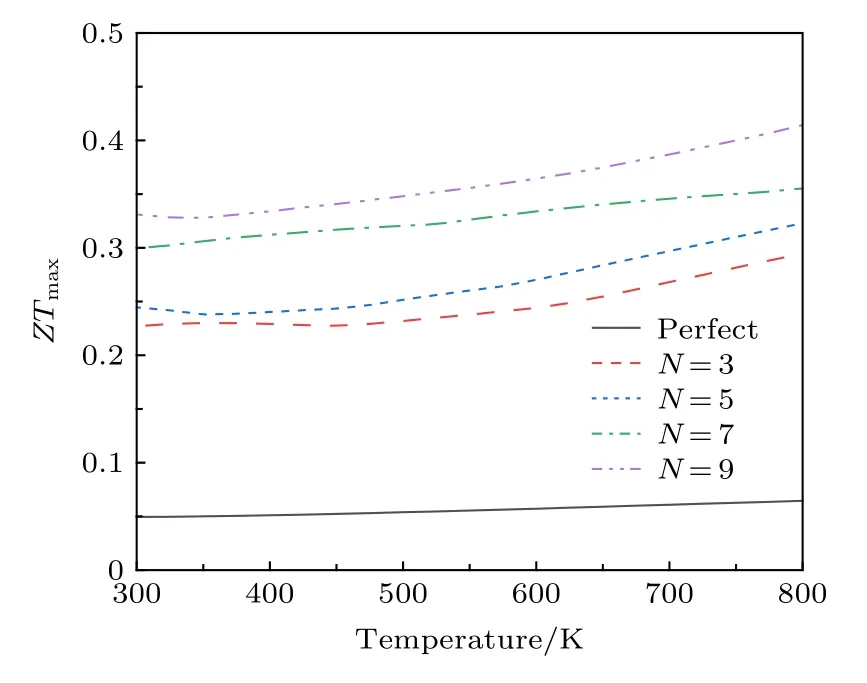
图4 完美和多晶石墨烯纳米带的热电品质因子随温度的变化Fig.4.Peak values of ZT as a function of temperature for perfect graphene nanoribbons and polycrystalline graphene nanoribbons.

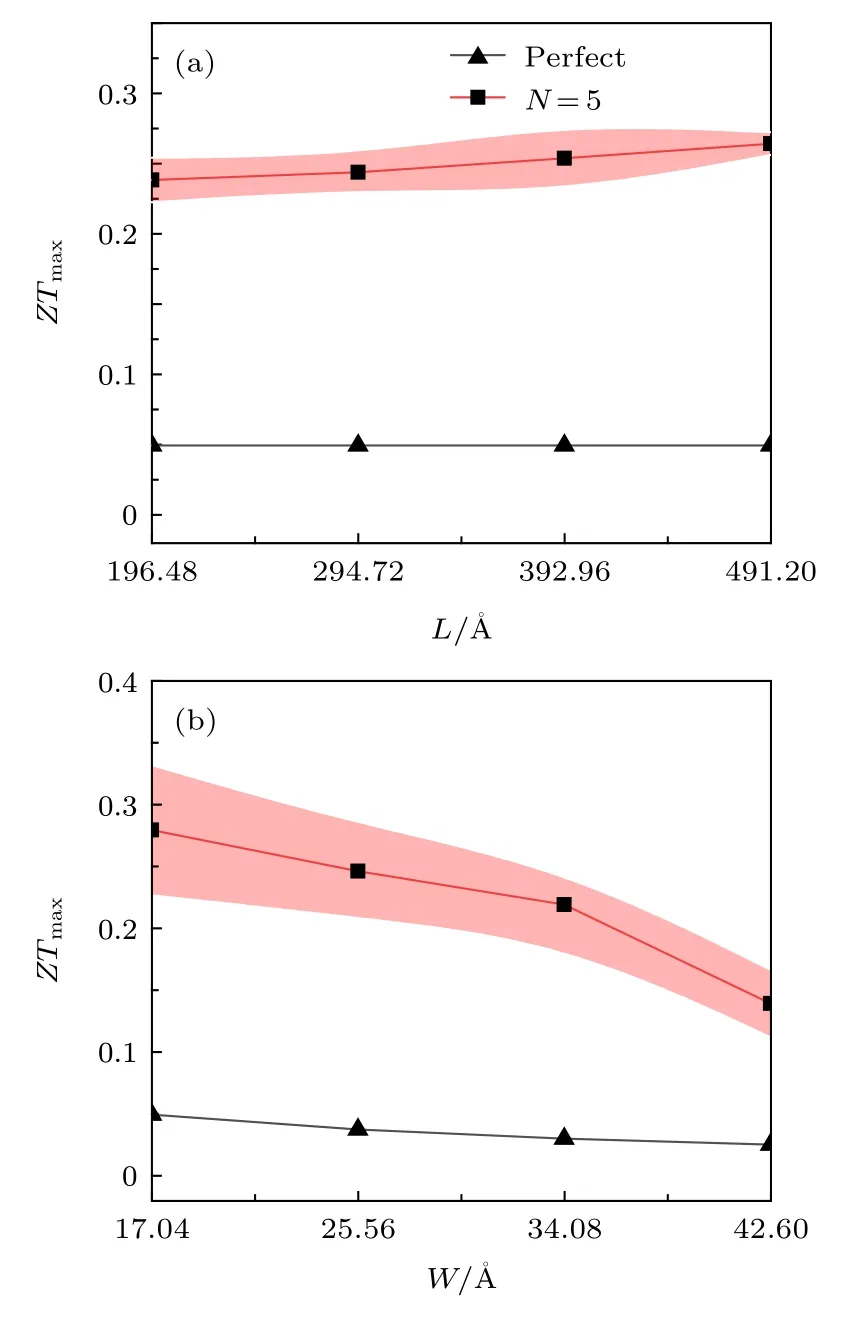
图5 室温下 (300 K), 完美与多晶石墨烯纳米带 (N = 5)热电品质因子随系统(a)长度L和(b)宽度W的变化(阴影部分为标准偏差)Fig.5.Peak values of ZT of perfect and polycrystalline graphene nanoribbons (N = 5) at room temperature as a function of (a) nanoribbon length or (b) nanoribbon width.The shading part corresponds to the standard deviation.

结合声子和电子输运性质的计算结果, 可以根据(11)式获得多晶石墨烯纳米带的热电品质因子,如图4所示.在室温下完美石墨烯纳米带的热电品质因子约为0.049, 这与先前的理论计算预测基本一致.当结构中引入晶界后, 可以看到热电品质因子得到了显著的提升.在室温下, 晶界的引入可将完美石墨烯纳米带的品质因子提高6倍左右(N= 7).然而, 从图4 还可以发现温度对于提升多晶石墨烯纳米带的热电转换效率并没有明显的积极作用, 这与先前对石墨炔热电性质的研究略有不同[34].随着晶界数目的增加, 多晶石墨烯纳米带热电性能还能得到进一步的增强.该结果表明多晶化的确是提升石墨烯纳米带热电性质的有效途径.最后研究了系统的结构尺寸对于多晶石墨烯纳米带热电性能的影响.如图5(a)所示, 在固定晶界数目前提下, 增加石墨烯纳米带的长度会进一步提高石墨烯纳米带的热电性能.这主要是由于单晶石墨烯晶粒长度的增加会使得低频(长波长)声子受到更多的散射.该行为将进一步削弱多晶石墨烯纳米带的热导, 进而增强其热电转换效率.对于宽度效应,从图5(b)中可以发现多晶石墨烯纳米带的热电品质因子会随着宽度的增加而逐渐下降.这主要归因于较宽的完美石墨烯纳米带本征热电性能低下所引起的.但是值得一提的是, 多晶石墨烯热电性能提升的倍率并未随着宽度的增加而显著下降.综上所述, 为了获得更为优异的热电性能, 应该选取较长的且宽度适中的多晶石墨烯纳米带.

4 结 论

本文采用非平衡格林函数方法系统地研究了晶界对石墨烯纳米带热电性能的调控作用.研究结果表明：晶界能有效地提高石墨烯纳米带的塞贝克系数, 同时可以极大地抑制其电子和声子热导.基于这两个积极的效应, 多晶石墨烯纳米带的热电转换性能得到了明显的增强.在室温下, 多晶石墨烯纳米带的热电品质因子约为0.3, 比完美石墨烯纳米带(约为0.05)提升了6倍左右.此外, 还发现晶界的数量以及系统的长度能进一步提升多晶石墨烯纳米带的热电性质, 而系统的宽度对其影响有限.这些研究结果表明多晶结构能够有效提升石墨烯纳米带的热电转换效率, 并为设计和制备基于石墨烯纳米带的热电器件提供了新的途径.