对称熔融拉锥型光纤光栅温度和应力传感特性*

涂兴华 赵宜超

(南京邮电大学电子与光学工程学院, 光电传感工程研究中心, 南京 210023)

锥形结构的光纤光栅具有对应力敏感而对温度不敏感的特性, 这可以有效抑制温度与应力的交叉敏感问题.提出一种利用熔融拉锥技术实现对称双锥形结构的光纤光栅, 结合传输矩阵法建立其传感特性理论模型并加以分析.首先研究影响啁啾系数变化的因素, 得到啁啾系数与光栅长度变化量的关系; 其次对对称熔融拉锥型光纤光栅的光谱特性进行分析, 讨论光谱短波长处出现密集调制现象的成因; 然后仿真研究温度和应力对对称熔融拉锥型光纤光栅的反射谱影响, 得到对应的中心波长和光谱宽度的变化关系.并针对应力灵敏度较低问题, 提出聚合物涂覆锥区增大传感锥区光纤半径差而进行增敏的方案, 利用熔融拉锥法制备对称熔融型光纤光栅, 通过实验验证理论仿真的正确性, 对称熔融拉锥型光纤光栅应力灵敏度为0.11391 nm/N.研究表明, 对称熔融拉锥型光纤光栅的啁啾系数与光栅长度变化量满足线性关系.对称熔融拉锥型光纤光栅端处光栅周期较小, 且反射率小于1, 左边透射光与右边反射光会产生干涉, 因此光谱短波长处会出现密集调制现象.随着轴向应力的增大, 光栅反射中心波长向长波方向移动, 光谱宽度变大, 且两者与轴向应力均满足线性关系; 随着温度升高, 反射谱峰中心波长向长波方向移动, 满足线性关系, 而温度对光谱宽度的影响可忽略不计.通过增大传感锥区光纤光栅半径差, 光纤光栅的应力灵敏度较之前提高了数百倍, 并且增大光栅长度变化量有助于进一步提高应力灵敏度.对称熔融拉锥型光纤光栅的光谱宽度只对应力敏感而对温度不敏感, 这一特性可用于实现温度与应力双参量测量.

1 引 言

光纤光栅具有耐腐蚀、低成本、灵敏度高等优点, 在传感领域发挥着越来越大的作用[1-3].均匀光纤布拉格光栅(FBG)存在的温度与应力交叉敏感[4,5]的问题阻碍光纤光栅得到更大的应用, 克服该问题是当前光纤光栅技术研究热点.

针对上述问题, 前人提出了多种解决方法, 如双波长光纤光栅法[6]、不同包层直径光栅组合法[7]、双折射布拉格光栅法[8]、保偏光纤光栅法[9]等, 但这些方法都存在着一定的缺点, 有些方案需要两根光栅, 成本高, 有些方案对工艺要求比较高.

锥形光纤光栅[10,11]是一种半径沿轴向位置变化的光栅结构, 轴向应力与锥形光纤光栅光谱宽度满足线性关系, 而不受温度影响, 克服了温度与应力交叉敏感问题.制作锥形光纤光栅的方法一般有两种.第一种是腐蚀法[12-14], 通过将普通的光纤光栅放入事先调配好的HF溶液中, 调控腐蚀时间,获得不同锥度的锥形光纤光栅.腐蚀法制成的锥形光纤光栅只有包层半径沿轴向变化, 纤芯半径不变, 初始光栅无啁啾特性.第二种是熔融拉锥法[15,16],利用氢氧火焰或高压放电等方法对光纤拉锥, 然后掩膜刻制均匀或啁啾光纤光栅.熔融拉锥法制成的锥形光纤光栅包层与纤芯半径同时沿轴向变化, 初始光栅具有啁啾特性.尽管以上两种方法制作的锥形光纤光栅的传感特性都已有广泛研究, 但通过对均匀FBG直接拉锥实现的双锥形光纤光栅的传输及传感特性研究尚未见诸报道.本文提出一种利用熔融拉锥技术, 对经过掺杂[17]、载氢[18]、退火等方式抑制“热擦除”效应[19,20]处理的FBG直接拉锥,形成具有对称双锥形结构的熔融拉锥型光纤光栅,其特点是不仅包层结构沿轴向发生变化, 纤芯也形成锥形, 相应的有效折射率及光栅周期也随之均沿轴向发生变化.基于传输矩阵法建立此对称熔融拉锥型光纤光栅的传感特性理论模型, 讨论分析其光谱宽度与温度和轴向应力的对应关系.最后针对应力传感灵敏度低的问题, 提出一种增加传感锥区光纤半径差进行应力增敏的方案.

2 理论模型

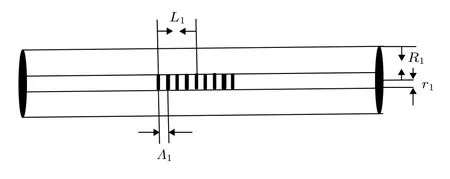
图1 普通均匀 FBG 结构Fig.1.Structure of normal uniform FBG.

图2 对称熔融拉锥型光纤光栅结构Fig.2.Structure of symmetric fused-tapered fiber grating.

对FBG实施熔融拉锥所形成对称熔融拉锥型光纤光栅是左右对称双锥结构.光纤光栅左半部分包层与纤芯直径沿光栅轴向方向线性减小, 右半部分则是线性增加.纤芯半径的变化导致光栅有效折射率沿轴向变化, 产生啁啾效果.在拉锥过程中,施加沿轴向周期性方向改变的力, 引起光栅周期变化, 啁啾现象愈加明显.FBG与对称熔融拉锥型光纤光栅结构分别如图1和图2所示.对称熔融拉锥型光纤光栅结构是以光栅中心左右对称, 因此下文涉及光栅长度及其变化量的参量, 其值均为总值的一半.L1是 FBG 光栅长度的一半,R1是 FBG 包层半径,r1是纤芯半径,Λ1是 FBG 光栅周期,L2是对称熔融拉锥型光纤光栅锥区长度的一半,R2是对称双锥区中心处的包层半径,r2是对称双锥区中心处的纤芯半径, 光栅长度变化量 ∆L=L2-L1.

采用传输矩阵法对双锥形光纤光栅进行分析,将光栅沿轴向分成M段, 每一段看成是一个完整且独立的均匀小光栅, 第i段均匀光栅的传输矩阵Fi[21]为

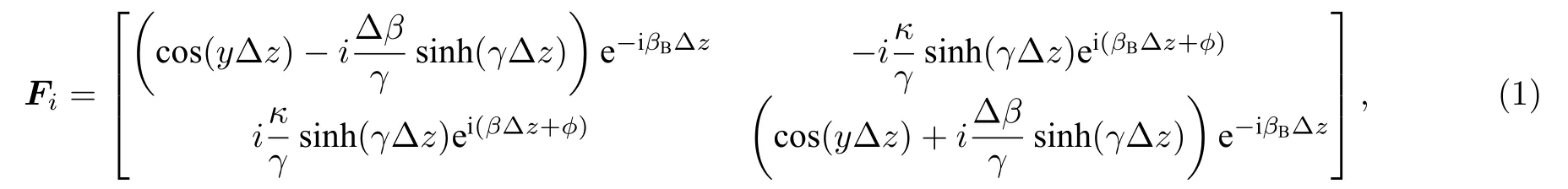
式中, ∆z表示每段均匀光栅的长度;βB= π/Λ;∆β是直流耦合系数, ∆β=ig/2+n2π/λ- π/Λ;κ是交流耦合系数,κ= π/λ∆n, 其中 ∆n是折射率调制深度;γ2=κ2-(∆β)2.因此整个锥形光栅的传输方程为

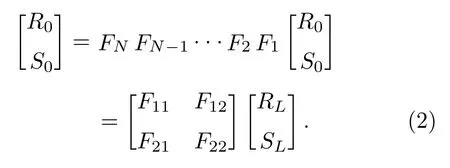
由初始条件RL=1 ,SL=0 得反射率为

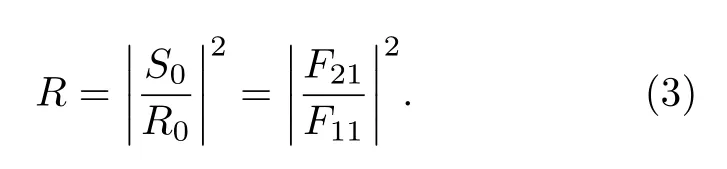
对称熔融拉锥型光纤光栅是左右对称双锥结构, 因此只需对左部分加以介绍.在拉锥过程中,施加沿轴向周期性方向改变的力, 引起光栅周期线性变化, 产生轴向啁啾.对称熔融拉锥型光纤光栅的光栅周期Λ2为

式中C是啁啾系数.光栅周期沿轴向线性变化, 运用数学递推知识, 得到啁啾系数C为

光纤光栅纤芯半径变化, 导致光栅有效折射率变化, 也会产生啁啾现象, 光栅有效折射率neff(z)[22]为

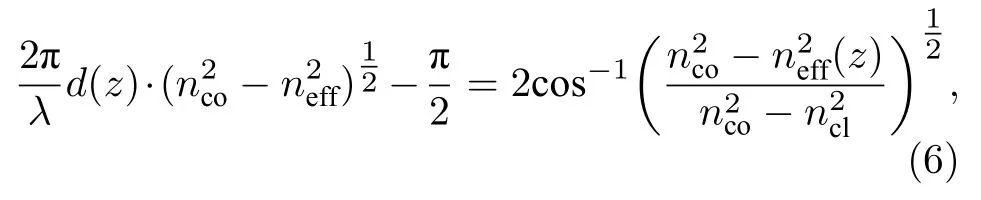
式中,d(z) 是纤芯直径,nco是纤芯折射率,ncl是包层折射率.

接下来讨论轴向应力和温度对该对称熔融拉锥型光纤光栅的影响.当光纤光栅受到轴向应力P作用时, 第i段光栅的光栅周期与有效折射率变化[23]分别为

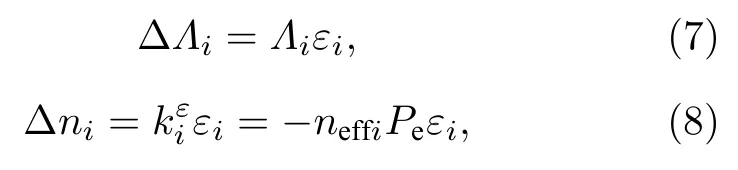
式中,Pe是光纤光栅的有效弹光系数;Λi是第i段光栅的光栅周期;neffi是第i段光栅的有效折射率;εi是第i段光纤光栅产生的应变,εi=P/ESi, 其中Si是第i段光栅的横截面积.

综上, 第i段光纤光栅的中心波长变化量 ∆λi为

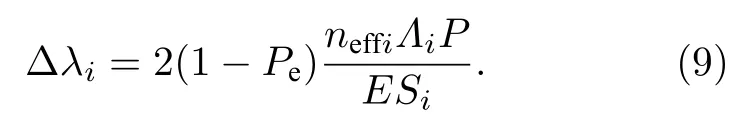
对称熔融拉锥型光纤光栅的反射光谱带宽变化量 ∆λFWHM为

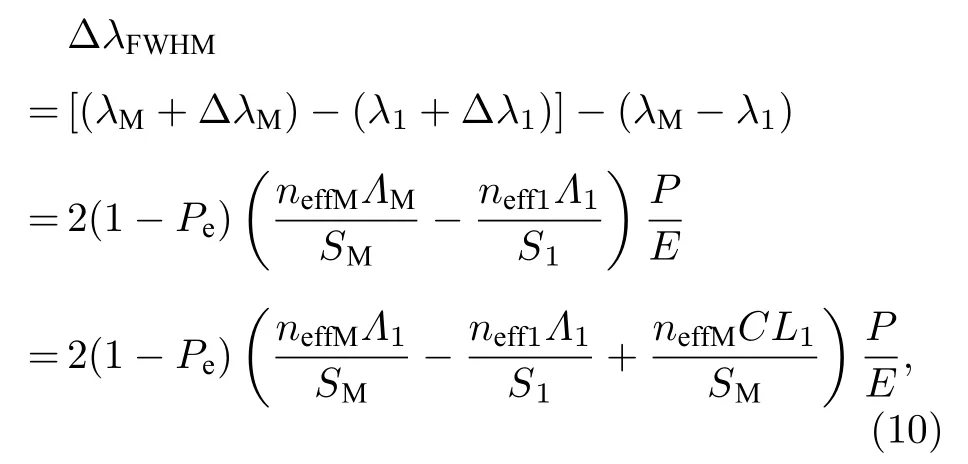
式中,SM和S1分别是光纤光栅中心位置与端处的横截面积,neffM和neff1分别是光纤光栅中心位置与端处的有效折射率,ΛM和Λ1分别是光纤光栅中心位置与端处的光栅周期.

当该光栅形成后, 光纤光栅的横截面积、光栅周期与轴向位置的关系式可以确定, 每段光栅的光栅周期和横截面积可以看作常数, 由(9)和(10)式可得, 反射中心波长变换量和反射谱带宽变化量与轴向应力P均满足线性关系.

当温度变化时, 第i段光栅的中心波长变化量[24]为

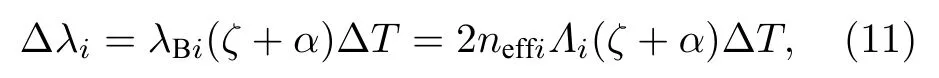
式中,ζ是热光系数,α是热膨胀系数, 则温度引起的光纤光栅的带宽变化量 ∆λFWHM为

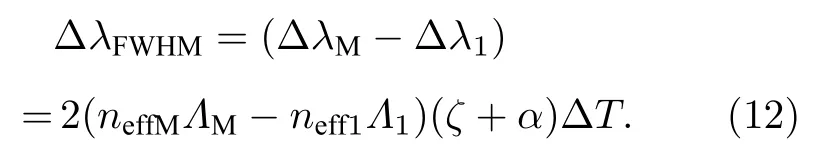
由(11)式可知, 温度变化量与中心反射波长变化量呈线性关系.从(12)式可得, 温度的变化也会导致光纤光栅反射光谱带宽的变化, 但变化量远小于应力导致的变化量, 可忽略不计.

3 仿真与分析

初始 FBG 的半光栅长度L1= 6 mm, 杨氏模量E= 70 GPa, 光栅周期Λ1=0.53×10-6, 纤芯折射率nco= 1.46 , 包层折射率nc1= 1.456 , 包层半径R1= 6.25 µm, 纤芯半径r1= 4.5 µm, 折射率调制深度 δneff=8×10-4.

3.1 应力大小与光谱宽度的关系

在研究应力与温度对光纤光栅反射谱影响之前, 先讨论啁啾系数C与FBG半光栅长度L1以及光栅长度变化量 ∆L的关系.从图3可以得出,FBG半栅区长度相同时, 光栅长度变化量与啁啾系数满足线性关系; 光栅长度变化量相同时,FBG半栅区长度越大, 啁啾系数越小.

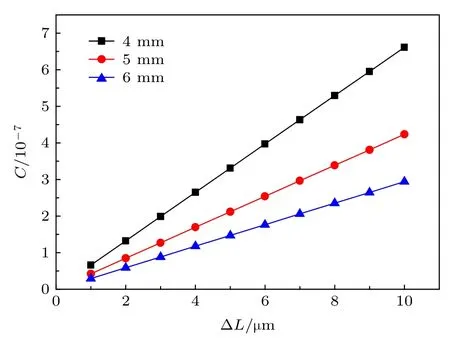
图3 啁啾系数随锥区长度及其变化量分布图Fig.3.Distribution of the chirp coefficient with the length of the cone and its variation.

选用FBG向两边各拉伸 ∆L=1 µm制成的对称熔融拉锥型光纤光栅, 并对其实施轴向应力进行应力传感模拟仿真, 研究应力大小对反射谱的影响.其中应力为 0 N (未施加应力) 和 2 N 时得到的反射光谱如图4所示.

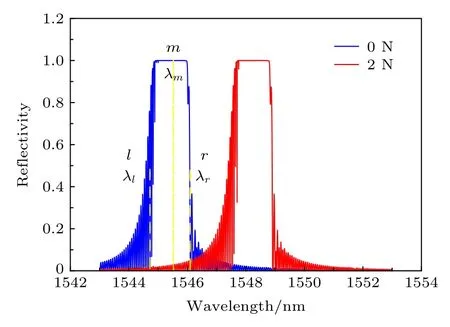
图4 光栅长度变化量 1 µm 的反射光谱图Fig.4.Reflectance spectra with the grating length variation of 1 µm.

从图4可以看到短波长处出现了较为密集的调制现象.这是因为在数值仿真时, 设计对称锥形光栅时引入线性啁啾使光栅周期呈现左半部分由密到疏、右半部分由疏到密的变化.光从光栅一端进入后, 光栅端处光栅周期较小, 短波长光被反射.但由于短波长位于反射谱的边缘处, 反射率小于1,因此有一部分短波长的光进入光栅继续传输, 在光栅的另一端又被反射回来一部分, 透射光与反射光干涉叠加, 出现图4短波长余弦调制现象.至于长波长处的光是被对称锥形光纤光栅中心部分的光栅反射, 中心部分的光栅周期最大, 二次反射的概率较小, 调制现象不明显, 长波长边沿与短波长边沿处相比更加陡峭.而反射谱的中间波长部分光,由于设计的光栅的轴向调制深度较大, 谱峰中心区域的反射率接近1, 不会出现调制现象.

由图4可得, 随着轴向应力不断增大, 反射谱中心波长向长波长方向移动, 并且光谱逐渐展宽,不过展宽量较小.

由于光栅反射谱左边部分出现密集调制现象,计算半高带宽误差较大, 因此取反射谱带宽的一半进行分析.如图4中黄线所示, 规定反射谱峰中心点为m点,m点对应光波长为中心波长λm, 光谱右边边沿谱峰值半高处记做r点, 其对应的光波长为λr, 光谱左边边沿谱峰值半高处记做l点, 其对应的光波长为λl, 则光谱半宽度为λr-λm或λm-λl, 下文λm,λr,λr-λm,λm-λl均以此为定义.

得到的中心波长λm和光谱半宽度λr-λm与轴向应力关系分别如图5和图6所示.从图5可知, 随着轴向应力的增大, 反射中心波长往长波长移动, 并与轴向应力满足线性关系.从图6可得,反射光谱半带宽逐渐增大, 且与轴向应力也是线性关系, 与 (9)和 (10)式相符, 不过灵敏度较低, 只有 8.35093 × 10—4nm/N.下文将介绍一种增敏方案, 并对光栅长度变化量与应力灵敏度关系加以分析.

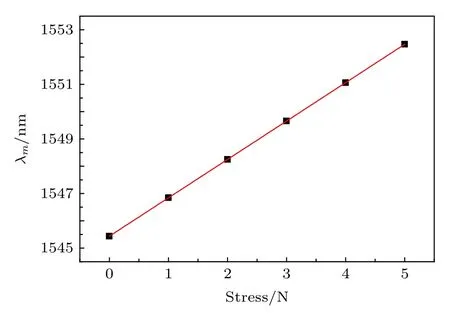
图5 中心波长随轴向应力变化分布图Fig.5.Distribution of center wavelength with axial stress.

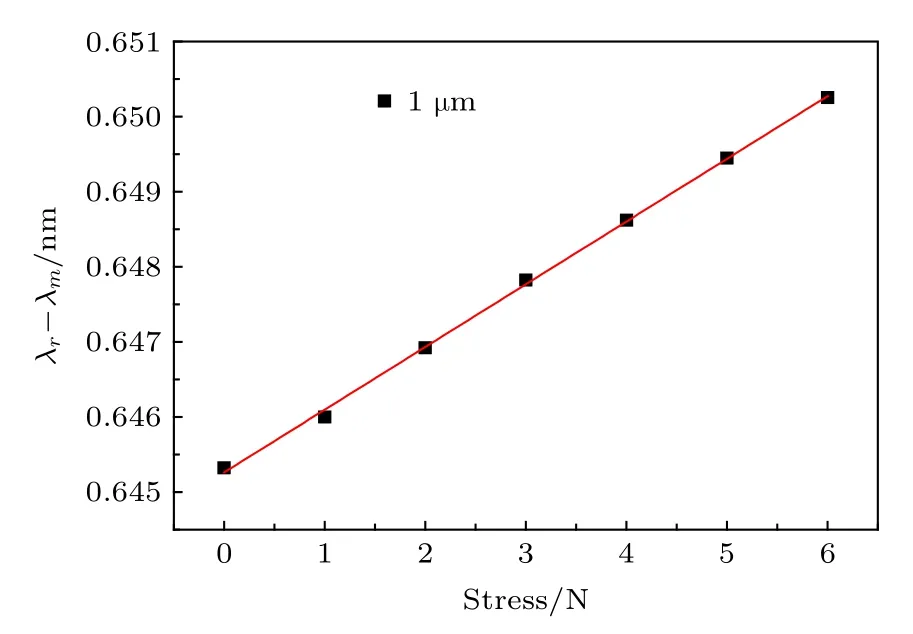
图6 光谱带宽半宽度随轴向应力变化分布图Fig.6.Distribution of half-width of the spectral bandwidth with axial stress.

3.2 温度与光谱宽度的关系

把上述对称熔融拉锥型光纤光栅引入不同温度场中进行温度传感模拟仿真分析, 仿真结果如图7所示.

由图7可知, 随着温度逐渐增大, 反射谱中心波长向长波长方向移动, 这与普通光纤光栅型温度传感特性是一致的.

而其光谱半宽度λr-λm与温度的关系如图8所示.

由图8可知, 反射带宽基本保持不变, 即温度的变化对光谱带宽的展宽影响极小, 可忽略不计.因此, 利用本文提出的对称熔融拉锥型光纤光栅的反射谱带宽特性可以很好地消除温度与应力的交叉敏感问题.

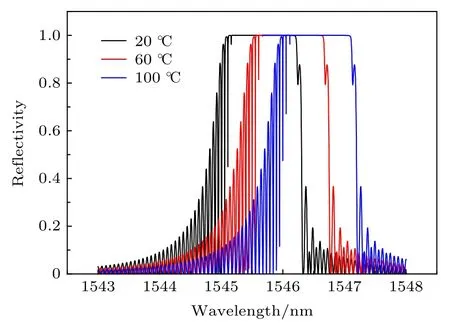
图7 光纤光栅在不同温度下的反射谱Fig.7.Reflection spectra of fiber grating at different temperatures.

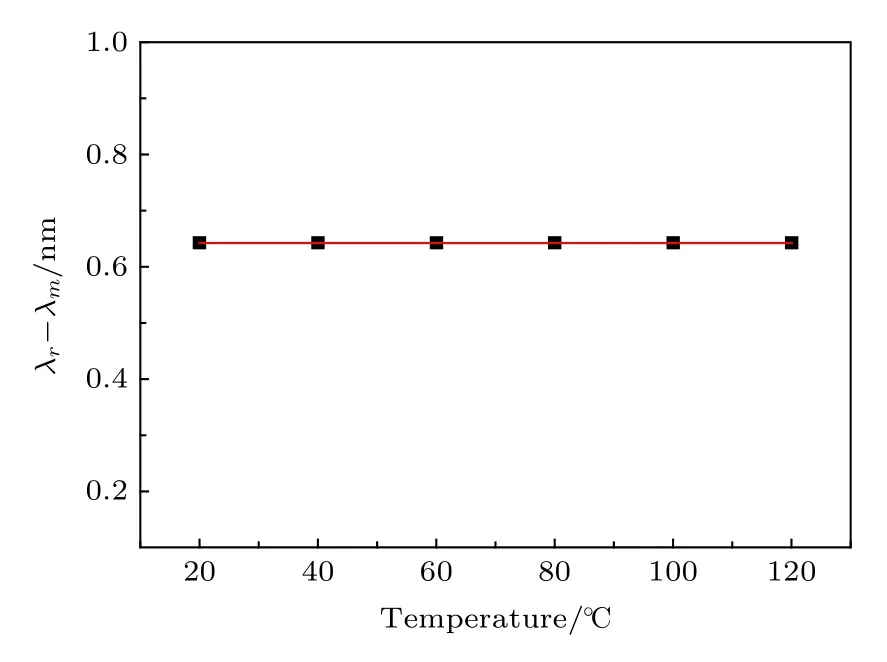
图8 光谱带宽半宽度随温度变化分布图Fig.8.Distribution of spectral bandwidth half-width with temperature.

3.3 增敏分析

由图6可以看到利用该对称熔融拉锥型光纤光栅的谱宽对应力的传感灵敏度很低, 只有8.35093 × 10—4nm/N, 远远不能满足实际需求, 因此需要对光纤光栅进行应力增敏.由(10)式可知,光栅端处横截面积S1和光栅中心处横截面积SM的倒数之差 (1 /SM-1/S1)越大, 则轴向应力与光谱宽度变化量关系式斜率越大, 即应力灵敏度越高.由(12)式可知, 1 /SM-1/S1的增大不会对温度灵敏度产生影响.因此, 将聚合物涂覆在该对称熔融拉锥型光纤光栅的表面, 光栅端处半径由R2增大到R3, 光栅中心处的半径不变, 并且其厚度沿光栅锥形区域也呈锥形变化, 即增大 1 /SM-1/S1值.其整体也类似于该锥形光栅结构, 以中心点左右对称, 如图9所示.

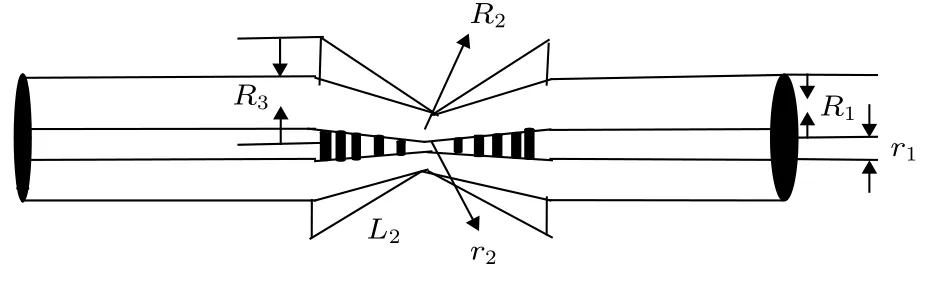
图9 对称熔融拉锥型光纤光栅涂覆聚合物后结构图Fig.9.Symmetric fused-tapered fiber grating coated polymer structure.

选用L1=6mm 的FBG参数, 仿真分析其不同拉伸长度即不同光栅长度变化量下的应力传感特性, 光栅长度变化量 ∆L分别为 0.5, 1, 1.5 µm.下文选用涂覆聚合物材料为聚丙烯酸酯, 其杨氏模量小于光纤杨氏模量, 使光纤光栅熔锥端处的半径由 62.5 µm 增大到 0 µm, 而光栅中心处的半径保持不变.

当 ∆L= 1 µm 时, 不同应力下的光栅反射光谱图如10所示.

如图10 所示, 增大 1 /SM-1/S1值后, 随着轴向应力的增大, 可以看到光栅反射谱的带宽明显变宽, 与(10)式理论相符.

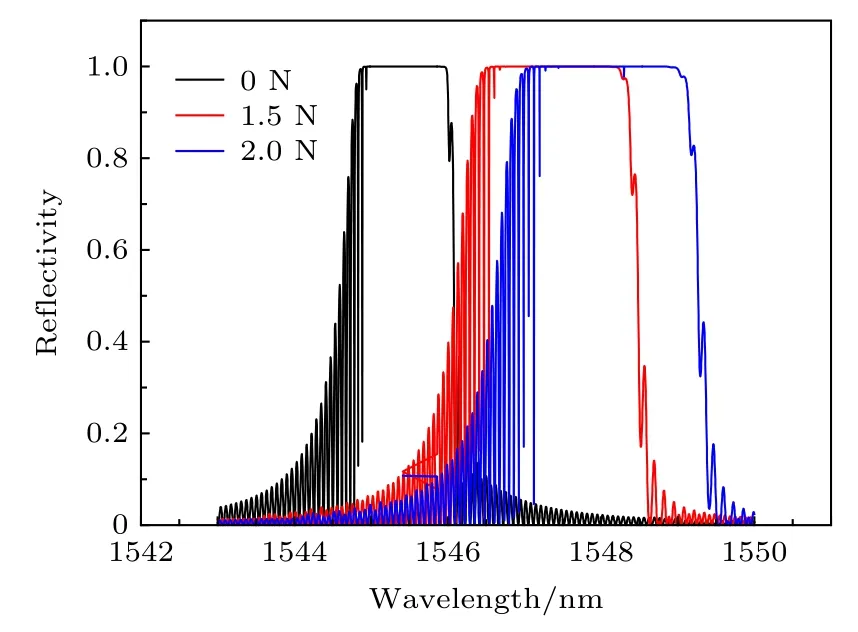
图10 增敏后的光纤光栅在不同应力下的反射谱Fig.10.Reflection spectra of sensitized fiber grating under different stresses.

类似地, 得到不同光栅长度变化量 ∆L所对应的光谱半宽度λr-λm与轴向应力P关系曲线图,如图11所示.

从图11 可以得出, 当 ∆L为 0.5, 1, 1.5 µm 时,应力灵敏度分别是 0.308105, 0.31836, 0.3426 nm/N.相对于L1=6mm , ∆L= 1 µm参数条件下的未增敏光栅结构, 增敏后的应力灵敏度达到0.31836 nm/N,较未增敏前提高了382倍.

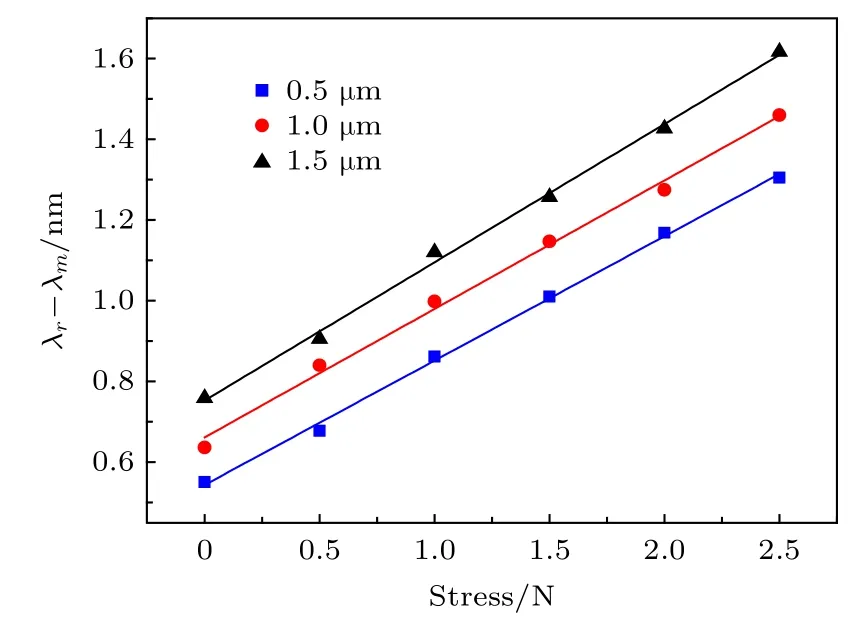
图11 光谱带宽半宽度随轴向应力变化分布图Fig.11.Distribution of half-width of the spectral bandwidth with axial stress.

由前述图3可知, 随着光栅长度变化量增大,啁啾系数增大.而由图11可以看到, 应力灵敏度也会随之不断增大, 因此光栅长度变化量增大有助于进一步提高应力灵敏度.但啁啾系数增大会造成光谱宽度展宽, 不利于中心波长检测以及实际应用测量.

3.4 实验研究

应力传感特性实验系统如图12所示.选用不同重量砝码块, 给光纤光栅施加轴向应力.40, 60,80, 100, 120, 140, 160 g 质量对应的重量分别是0.392, 0.588, 0.784, 0.98, 1.176, 1.372, 1.568 N.首先, 本实验采用古河S178A型熔接机来制备对称熔融拉锥型光纤光栅.将反射中心波长为1549 nm的均匀光纤光栅的中间位置对准熔接机放电位置.熔接机的电流设置为 9 mA, 放电时间为0.3 s.在放电熔融时, 向该光纤光栅的两端施加轴向拉力, 然后多次放电, 形成对称熔融拉锥型光纤光栅.

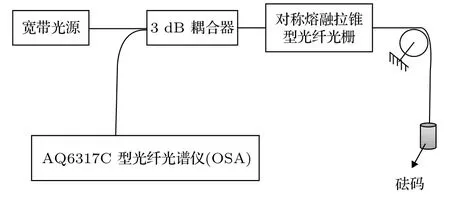
图12 应力传感实验系统图Fig.12.Stress sensing experimental device.

给光纤光栅施加轴向应力为0.392, 0.784,1.176 N时, 对应的反射谱如图13所示.

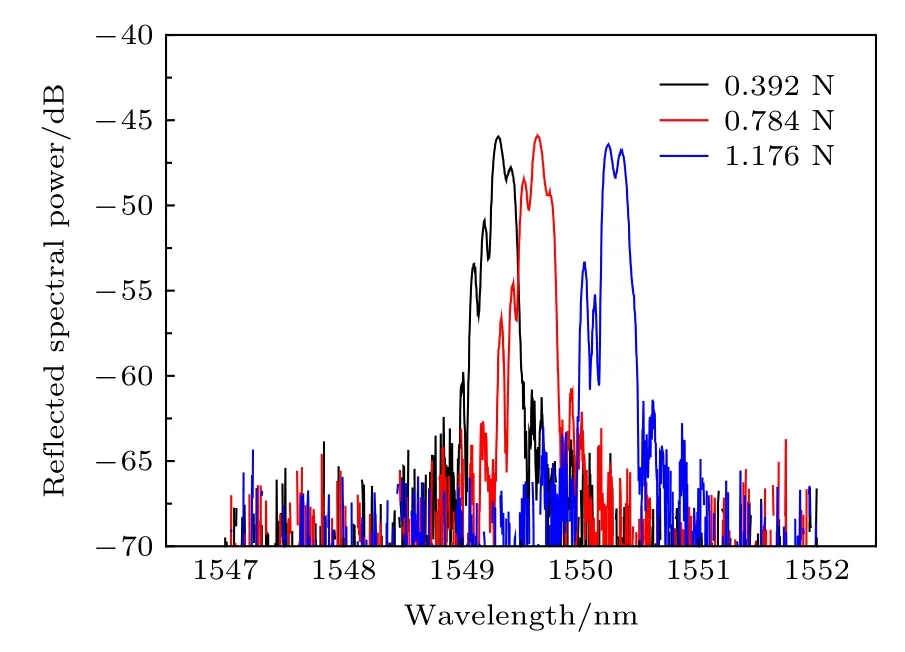
图13 光纤光栅在不同轴向应力下的光谱图Fig.13.Spectral diagram of fiber grating under different axial stresses.

从图13可以看出, 随着轴向应力的增大, 对称熔融拉锥型光纤光栅的反射谱向长波长方向移动, 并且光谱展宽.

接下来研究温度对对称熔融拉锥型光纤光栅传感特性的影响, 实验装置与应力系统基本一致,只是将滑轮模块取消, 然后把光纤光栅放置于水浴设备中, 采用水浴法改变温度.不同温度下对称熔融拉锥型光纤光栅反射谱如图14所示.

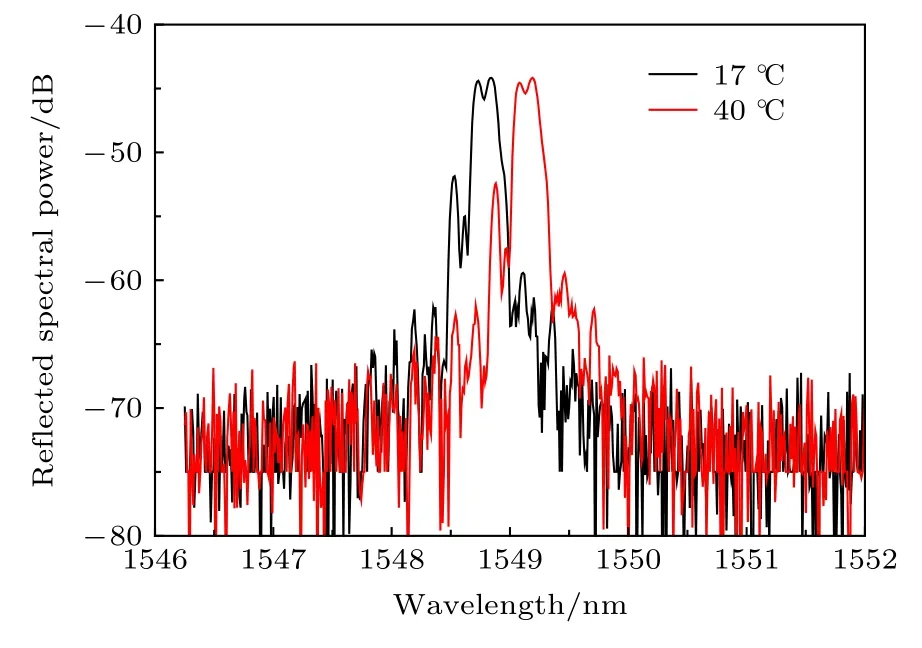
图14 光纤光栅在不同温度下的反射谱Fig.14.Reflective spectra of fiber grating at different temperatures.

由图14可看到, 随着温度的提高, 对称熔融拉锥型光纤光栅的反射谱中心波长沿长波长方向移动, 且光谱不展宽, 光谱宽度保持不变.

根据实验数据, 可以得到光谱半宽度λl-λm与温度及应力F的关系如图15所示.

由图15可以看到, 温度改变时, 光谱半宽度会有较小变化.随着温度的增加,λl-λm的测量值并不随之增大, 而在原谱宽值上下起伏变化, 这是由于测量误差造成, 说明温度对光谱带宽的影响可忽略.而随着轴向应力的不断增大,λl-λm则明显随之增大, 且两者满足线性关系.经过二项式线性拟合, 如图15 所示, 线性拟合度为 0.91441, 斜率为0.11391.则可得到轴向应力的灵敏度方程为

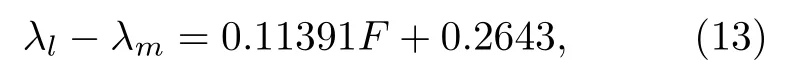
即轴向应力的灵敏度为0.11391 nm/N.由于实验采用是普通均匀光纤光栅进行熔融拉锥制备, 没有采取额外的消除“热擦除”效应措施, 导致反射率降低, 其反射谱出现较大的旁瓣, 因此测量数据会产生一定的误差.

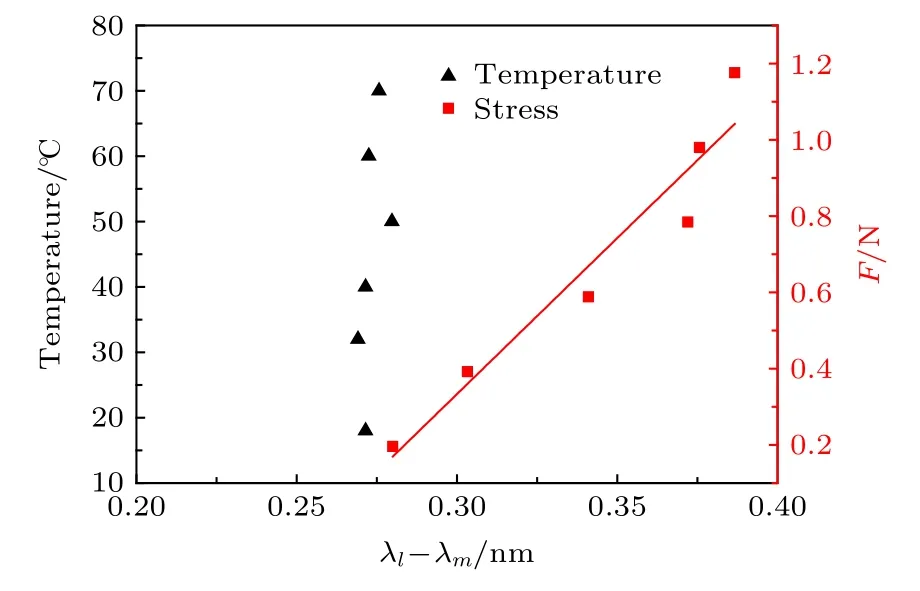
图15 温度与应力对 λl-λm 的影响Fig.15.Effects of temperature and stress on λl-λm .

4 结 论

提出一种利用熔融拉锥技术实现对称双锥形结构的光纤光栅.首先建立了对称熔融拉锥型光纤光栅的理论模型, 结合传输矩阵法, 数值仿真得到其在不同应力场和温度场下的反射谱特性.其光栅反射谱带宽与轴向应力满足线性关系, 而温度对光谱宽度的影响可忽略.针对应力灵敏度较低问题,提出一种采用聚合物涂覆增大传感锥区光纤半径差而进行增敏的方案, 应力灵敏度可以提高两个数量级.而且采用聚合物涂覆方式, 既可以增敏, 又可以有效地对拉锥后的光栅进行保护, 提高其实用可能性.增大光栅长度变化量有助于进一步提高灵敏度.

最后实验研究了基于熔融拉锥法制备的对称熔融拉锥型光纤光栅的传感特性, 得到温度和应力参量与其光谱特性的反演关系.利用其中心波长与温度和应力的线性反演关系, 以及谱线带宽与应力的线性关系, 可以实现温度与应力双参量测量, 为解决温度与应力交叉敏感问题提供了一种有效的方法.