基于马尔可夫模型的云系统安全性与性能建模

许瀚 罗亮 孙鹏 孟飒

摘 要：针对云环境缺乏安全性评估的问题，提出一种评估系统安全性的建模方法，并建立了云环境下的安全性性能（SP）关联模型。首先，针对云系统中最重要的组成部分，即虚拟机，建立了评估其安全性的模型，该模型充分反映了安全机制和恶意攻击两个安全因素对虚拟机的影响;随后基于虚拟机与云系统之间的关系，提出评估云系统安全性的指标;其次，提出一种分层建模方法来建立SP关联模型。利用队列理论对云计算系统的性能进行建模，然后基于贝叶斯理论和相关分析建立了安全性和性能之间的关联关系，并提出评估复杂SP相关性的新指标。实验结果验证了理论模型的正确性，并揭示了安全因素引起的性能动态变化规律。

关键词：云计算;安全性建模;性能建模;马尔可夫模型;排队论

中图分类号：

TP309.2文献标志码：A

Cloud system security and performance modeling based on Markov model

XU Han*， LUO Liang， SUN Peng， MENG Sa

College of Computer Science and Engineering， University of Electronic Science and Technology of China， Chengdu Sichuan 611731， China

Abstract：

Aiming at the lack of security assessment in cloud environment， a cloudbased security modeling method was proposed，and a SecurityPerformance （SP） association model in cloud environment was established. Firstly， a model was constructed for virtual machines， the most important component of the cloud system， to evaluate its security. The model fully reflected the impact of security mechanisms and malicious attacks on virtual machines. Secondly， based on the relationship between virtual machine and cloud system， an indicator was proposed for assessing the security of the cloud system. Thirdly， a hierarchical modeling method was proposed to establish an SP association model. Queuing theory was used to model the performance of cloud computing systems， and the relationship between security and performance was established based on Bayesian theory and association analysis， and a new index for evaluating the association of complex SP was proposed. Experimental results verify the correctness of the theoretical model and reveal the dynamic change rule of performance caused by safety factors.

Key words：

cloud computing; security modeling; performance modeling; Markov model; queuing theory

0 引言

在云計算系统（Cloud Computing System， CCS）中，服务质量（Quality of Service， QoS）是从提供商和客户角度来看的重要服务评估标准，它直接影响云提供商的客户体验和利润。 因此，对QoS的精确评估可以帮助云提供商开发合理的资源分配策略以改善客户端体验。 通常采用性能度量来量化QoS。 人们已经广泛研究了许多用于评估性能的方法和方法，但是，另一个重要的指标，即安全性，在评估QoS时没有得到足够的重视。 更重要的是，安全性还会对性能指标产生严重影响，即复杂的SP相关性。CCS动态地组织虚拟机（Virtual Machine， VM）和服务器以运行一系列服务，其中每个服务被分离为在VM上并行执行的一组任务。虽然动态组织和并行执行使CCS有效地完成了服务，但它也给CCS安全带来了严重的问题。由于CCS的虚拟化，VM安全性成为传统系统中不存在的新安全因素。VM的安全性具有一些相似的特征，例如，不同的VM完全隔离，并且共存的VM可能由于对其主机服务器的攻击而同时失败。同时，VM安全性在最近的研究中也备受关注。 文献[1]的研究表明，

在基础架构即服务（Infrastructure as a Service， IaaS）级别上，

大多数特定于云的攻击通过受到攻击的VM威胁CCS，例如VM侧通道攻击、对虚拟机管理程序的VM攻击、对运行中VM进行磁盘注入等攻击方式。

下面简要介绍以上列举的攻击行为：

1）VM侧通道攻击通常基于VM漏洞[2]。它代表了利用VM共存的一类攻击，当两个或多个用户的VM共享相同的硬件时会出现这种共存。

2）通过虚拟机管理程序的VM攻击从受感染的VM开始[3]。攻击者可以从已感染的VM获取有效的用户凭证（通过捕获、监视或使用恶意软件）。然后，攻击者可以获得公共云账户以危害虚拟机管理程序，并从公共云中存在的相关攻击路径访问目标共同驻留机构的其他VM。

3）对运行中VM进行磁盘注入这种攻击方式，攻击者试图通过将恶意代码放入目标VM的本地连接存储中，以此来获取对目标数据的访问权[4]。很明显，如果攻击者愿意，他们的行为将通过受到攻击的虚拟机对CCS的QoS产生巨大影响。VM安全性严重影响了CCS的安全性，因此，为确保云计算在现实环境中的应用，如何评估CCS安全性并评估其对QoS度量的影响（如服务性能）是必须解决的关键问题[5]。

近年来，已有许多用于量化QoS的性能度量方法的成果。文献[6]中提出了用于评估基础架构即服务（Infrastructure as a Service， IaaS）、平台即服务（Platform as a Service， PaaS）、软件即服务（Software as a Service， SaaS）以及混搭或混合云的通用云性能模型。作者使用现实生活中的基准程序测试云，并提出新的性能指标。文献[7]研究了云计算环境中利润最大化的最优多服务器配置问题。在这种方法中，作者构建定价模型并将多服务器系统视为M/M/m排队模型，以制定和分析解决优化问题。文献[8]中开发新的性能模型并运行HiBench基准测试，以测试各种弹性计算云（Amazon Elastic Compute Cloud， EC2）

配置上的Hadoop性能，并评估三种扩展策略，以提升弹性云（如EC2）的性能、效率和生产率。在这种方法中，性能模型的构造与文献[7]中的相同。但是，在这些方法中没有考虑安全性对性能的影响。

安全性要求通常与性能要求形成对比[9]：

一方面，安全机制的操作不可避免地消耗一定量的资源，例如CPU时间和存储器，从而增加了服务的执行时间;另一方面，恶意攻击可能导致服务器或VM故障并导致服务故障或超时故障。目前，现有的系统安全性研究常常把安全机制和恶意攻击对系统的影响分开来考虑。文献[10]中提出了一种QoS驱动的方法来研究安全机制对不同系统性能的开销;但是，作者还没有研究恶意攻击对性能的影响，这将导致性能评估的不准确性。在文献[11]中，建模方法用于提供基于上下文的模型以平衡QoS和安全性;但是，这些研究并未系统地解决恶意攻击对性能的影响。文献[12]中构建一个多排队模型，以整体地描述三种类型的攻击，并研究特定电子邮件安全系统的性能指标;但是，安全机制的资源消耗尚未得到彻底解决。

为解决以上所提问题，本文针对可用性这一安全性因素对服务性能的影响进行研究，提出了一种分层建模方法，通过建立安全性和服务性能之间的联系来全面地反映云系统中安全性对服务性能的影响。首先，给出了CCS的物理和逻辑结构;随后，分别介绍了对CCS进行安全性和服务性能建模的方法;最后，给出了仿真实验用以验证所提分层建模方法的正确性，并揭示不同强度的安全机制对服务性能的影响。

1 云计算系统的结构

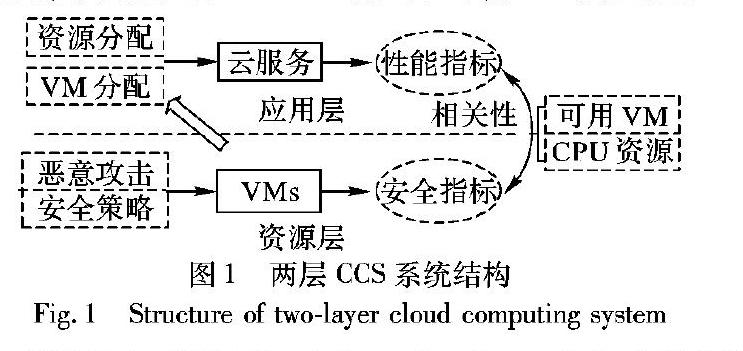
图1显示了CCS的部分系统结构。CCS中最基本的层是资源层，其中包含所有硬件和软件，包括存储、服务器基础架构和虚拟基础架构。在资源层中，CCS以VM为单位组织资源，这些VM资源是CCS上的高度自动化的系统单元。 VM通常可以通过互联网单独访问[13-14]。此功能使VM容易受到恶意攻击，例如，常见漏洞和暴露（Common Vulnerabilities and Exposures， CVE）主动标识漏洞（CVE20074593），使攻击者经由vstor2WS60.sys设备驱动程序在虚拟机（VMWare的）工作站6.0上进行拒绝服务（Denial of Service， DoS）攻擊[15]。 DoS攻击可以减慢一些关键进程并导致失败。显然，VM安全性是CCS不可避免的漏洞，因此，评估VM安全性（包括从恶意攻击中学习威胁并分析防御机制的行为）可以帮助提高云安全性甚至提高服务性能。值得注意的是，恶意攻击是随机的。理论建模方法可以根据抽象的特征和宏观统计的观点来捕捉这种随机性。众所周知，马尔可夫模型理论已广泛应用于安全评估领域。例如，文献[12，16-17]中使用它进行研究。因此，本文建立了Markov模型来评估VM安全性。

在应用层中，COS（Cloud Operating System）负责服务请求的分配和结果的收集。

从COS返回给用户的请求数可以是用于描述CCS的服务性能的指标。因此，在本文中，服务性能定义为每单位时间完成的请求数。如上所述，VM对服务处理有很大影响：一方面，当虚拟机的可用性受到恶意攻击的威胁时，虚拟机可能无法处理子任务并导致子任务的处理失败。更严重的是，恶意攻击可能会减少可用虚拟机的数量，并导致可用虚拟机太少时发生任务溢出故障。另一方面，在VM中启用安全机制会消耗一部分CPU资源并减少用于处理子任务的CPU资源，最终，它可能会延长子任务的处理时间并导致超时失败。通常，安全性通过影响VM的可用VM数量和CPU处理能力来影响服务性能，因此，这两个参数可以成为安全性和性能之间的桥梁。

众所周知，安全机制的CPU占用取决于其算法复杂性或安全级别，例如加密机制和分层保护域。对于加密机制，密钥长度表示算法复杂度和加密机制的安全级别，并确定包括加密和解密在内的动作的CPU占用时间。对于分层保护域，安全级别确定用户状态和内核状态之间切换的频率和CPU占用时间。为了更好地描述算法的复杂性或安全级别，“强度”已被用于当前可靠性和安全性研究领域[10]。因此，“强度”也用于定义本章中算法复杂度或安全机制的安全级别。安全机制被定义为三种强度，即“高”“中”和“低”。强度越高，安全级别越高，算法越复杂。如果VM应用高强度安全机制，则与应用中强度或低强度安全机制相比，子任务的完成时间增加。

2 资源层中的安全性建模

安全性通常包括可用性、保密性、完整性等内容，本文主要针对系统VM受攻击后的工作状态来定义系统安全性，因此本文将从可用性的角度出发来评估系统的安全性。

2.1 模型建立前提条件

基于以下前提条件，Markov模型可用于对VM安全性进行建模：

1）大多数攻击都是无组织和自发的，因此，攻击的到达时间是随机的。 这种随机性可以通过适当的到达过程来描述，例如泊松分布[12，16-17]。

2）安全机制具有一系列规范化操作来抵御攻击。 文献[12，16-17]指出，

这些操作的时间服从指数分布。

注意，在马尔可夫模型中，某些状态的逗留时间的分布函数可能是非指数的。 因此，潜在的随机模型需要根据半马尔可夫过程（SemiMarkov Process， SMP）来制定[17]。

2.2 虚拟机安全性建模

图2显示了受攻击的VM的状态转换图。在该状态转换图中有三种状态：良好状态（G）、受攻击状态（A）和失败状态（F）。状态G表示VM处于可以提供可靠服务的良好状态;状态A表示VM处于受攻击影响的状态，但此时VM仍然可以提供服务;状态F表示VM处于受攻击影响已经失效，无法提供服务的状态。在图2中，

P1、P2、P3和P4是状态转移概率，它们的取值取决于安全机制的强度和攻击。P1表示VM处于G状态中的概率;

P2表示在安全机制未能抵御攻击的情况下VM的状态从A变为F的概率;P3=1-P1表示当安全机制成功抵抗攻击时，VM的状态从A变为G的概率; P4=1-P2表示当攻击影响VM时，VM的状态从G变为A的概率。另外，不考虑VM的状态从G变为F的情况。这是因为云服务提供商通常非常注重安全性，这使得攻击者很难在不被注意的情况下使VM无效。注意F是吸收状态，这意味着不能从该状态改变到任何其他状态。在真实环境中，安全机制可能不够强大，无法抵御攻击。发生这种情况时，除非系统管理员采取紧急措施，例如重新启动、切断互联网访问等，否则系统无法恢复正常。因此，虚线用于描述在激活那些紧急动作之后VM的状态从F变为G的情况。

现在，可以通过求解此状态转换图来进行VM安全性评估。在此，定义Na（x，n）和Pa两个安全指标，其中：Na（x，n）表示n个VM中有x个VM可用的概率;Pa表示VM可用的概率;n是VM的总数;x是可用VM的数量;x≤n。

Na（x，n）和Pa分别用于评估整个系统和一个VM的安全性。值得注意的是，Pa是计算Na（x，n）的前提条件。

Pa的求解过程如下：

首先将VM的状态分别定义为可用集xa和不可用集xua。

如果VM的状态属于xa，则此VM可用;

否则属于xua，VM不可用。

在本文中，G和A被分类为集合xa，F被分类为集合xua。其次，ПG、ПA和ПF分别被定义为状态G、A和F的稳态概率。

因为∑i∈（G，A，F）πi=1，所以通过式（1）即可求解Pa：

pa=πG+πA=1-πF

（1）

本文采用文献[17]方法

来求解图2所示的SMP模型，πi{i∈（G，A，F）}可由如下公式计算：

πi=vihi∑ivihi

（2）

其中：vi{i∈（G，A，F）}是图2中所示的嵌入离散时间马尔可夫链中的状态的稳态概率，并且hi{i∈（G，A，F）}每个状态的平均逗留时间。

vi的计算公式如下：

=P

（3）

其中：=[vG vA vF];

P是转移概率矩阵。

估算P和hi的值有两种方法：第一种方法是使用先验知识和攻击实验;第二种方法是使用参数训练方法，该方法取决于预定义的Pa值和模型（本文的实验部分就是采用这种方法）。

在此简单介绍一下第二种方法。在某些情况下，安全机制和攻击的先验知识是有限的，因此在一段时间内，

只能从系统日志中获取VM故障数和攻击时间的数据。

然后，可以使用通过这些统计数据，合并使用概率理论，即可求得来计算Pa。

最后，P和hi的值可以通过Pa参数训练方法获得。

如前所述，Pa是计算Na（x，n）的前提条件。

如果分配了x和n，并且每个VM的Pa是已知的，则可以计算Na（x，n）。

容易理解，可用VM的数量有Cxn种组合。根据贝叶斯理论，通过对每种组合的概率求和，即可求解Na（x，n）。

以計算Na（3，5）的值作为说明。Na（3，5）表示在CCS中总共有5个VM（1号到5号），其中只有3个可用，恶意攻击使另外两个不可用。 在这种情况下，不知道哪三个可用。 事实上，每种组合都有可能发生。 例如：可能是1～3号可用，而4～5号不可用;也可能是2～4号可用，而1、5号不可用。 因此，应考虑所有可能的组合来计算Na（3，5）。在对所有可能组合的概率求和并计算平均结果之后，获得Na（3，5），计算公式如下：

N1a=p1ap2ap3a（1-p4a）（1-p5a）

其他可能组合的计算公式也可用相同的方式计算。

将这些组合的结果相加求和，并除以这些组合的数量（C35），即可得到Na（3，5），计算公式如下所示：

Na（3，5）=N1a+N2a+N3a+…+NC35aC35

该方法，即可求得Na（x，n）。

3 应用层中的性能建模与SP关联指标

3.1 模模型建立前提条件

排队理论已广泛用于模拟真实环境中随机事件的到达完成过程，因此选用M/M/S排队模型来描述CCS中任务的到达完成过程。 M/M/S表示任务的到达遵循泊松分布，子任务的服务时间遵循指数分布，任务的队列长度是有限的。

为了便于计算，本文假设：

1）同一信任区域（Trust Zone， TZ）中的所有VM（构成了一个网段（network segmentation）[1]）采用具有相同强度的统一安全机制。在真实的云环境中，CCS由许多互连的TZ[1]组成。 TZ的设置是为了便于管理和处理不同类型的任务，其中用户请求通常会租用多台相同类型的VM实例。因此，假设所有VM在同一TZ中应用相同的安全机制是可行的。

2）VM和CPU遵循一对一的逻辑映射机制，这在CCS中很常见。

3）在VM中，一次只执行一个任务。

4）任务队列遵循先来先服务（First Come First Service， FCFS）的规则。

5）当所有可用的VM都忙时，新到达的任务应该在任务队列中等待。如果任务队列中的任务数等于任务队列的最大长度，则放弃新到达的任务。

3.2 云计算系统性能建模

图3用生灭过程展示了任务队列的执行过程。该任务队列的参数定义如下。

1）f-dj是VMj中运行的安全机制的CPU占用率。

2）λ是任务的到达率，可以定义为每单位时间到达任务的数量。例如，λ=2.1s-1。

3）fj是VMj中除安全机制占用的部分之外的可用CPU速率， fj≤1-f-dj。

4）n是VM的数量，包含所有可用和不可用VM的数量。

5）x是可用VM的数量，x≤n。

6）L是任务队列的最大长度。

7）μ是未应用任何安全机制的VM的最大服务速率，可以定义为每单位时间完成的任务数。例如，μ=1.1s-1。

8）μe是有i个任务同时执行时的服务速率，i≤L。根据假设1，所有处在一个TZ中的VM应用相同的安全机制。因此，μi的计算公式为：

μi=i×1n∑nj=1μ（fj）; i≤x

（4）

μi=μx=∑xj=1μ（fj）; x

（5）

其中：

1n∑nj=1μ（fj）表示TZ中每个VM的平均服务速率;μ（fj）是VMj的服务速率，它是参数fj和μ的函数。 μ（fj）表示当运行的安全机制占用CPU的某些部分时VMj的处理任务的能力。

9）Te是任务的最大逗留时间。如果任务的逗留时间超过Td，则发生超时故障。

可以通过分析此任务队列模型来评估CCS的性能。 这里，性能指标被定义为δ（x），其中：x表示可用VM的数量;δ（x）表示每单位时间完成的任务数。任务完成意味着在任务的整个执行过程中没有发生超时故障。根据队列理论，δ（x）的计算公式为：

δ（x）=ηe（1-ptimeout）

（6）

其中：1-Ptimeout表示任务在整个执行过程中未发生超时故障，且已成功完成的概率;ηe表示新任务的有效到达率。有效到达意味着任务已被放置在任务队列中，而没有因到达后队列已满而被放弃。 因此，ηe可根据式（7）计算：

ηe=λ（1-qL）

（7）

其中：λ是任务的到达率;qL表示任务队列已满的概率。当队列已满时，将放弃新到达的任务，这意味着任务队列发生阻塞故障。为了计算qL，首先将qe定义为任务队列中现有i个任务的概率。通过图3构建ChapmanKolmogorov方程并求解该方程，

可以很容易得到qi。因此，qi可通过如下公式计算：

q0=1 + x-1i=1（λ）i∏ir=1μr + Li=x（λ）iμi-xx∏xr=1μr-1

（8）

qi=（λ）i∏ir=1μrq0; 1≤i

（9）

qi=（λ）iμxi-x∏xr=1μrq0; x≤i

（10）

根据式（10），可求得qL：

qL=pblock=（λ）LμL-xx∏xr=1μrq0

（11）

以上是ηe的解。下面对（1-Pe）进行求解。（1-Pe）表示任务的执行时间超过最大逗留时间Te的概率。

根据Ptimeout的定义，可知

ptimeout=Pr{Ts>Td}=1-∫ Td0fs（t）dt

（12）

其中：Ts表示任務的逗留时间，即任务的处理时间; fs（t）被定义为逗留时间Ts的概率密度函数（Probability Density Function，PDF）。 显然，Ts是任务执行时间Te和等待时间Tw之和。 因此， fs（t）的计算公式为：

fs（t）=∑xi=0Pr（i）·fe（t）+∑L-1i=x+1Pr（i）·fi-x+1（t）fe（t）

（13）

其中：“”代表两个函数的卷积运算符;Pr（i）是当新任务到达时，任务队列中有i个任务的概率。根据贝叶斯方法和式（8）～（10），Pr（i）的计算公式为：

Pr（i）=Pr{i|i

（14）

如前所述，任务的服务时间遵循指数分布。 fe（t）被定义为具有参数μe的执行时间Te的PDF，因此， fe（t）的计算公式为：

fe（t）=μi·e-μit

（15）

等待时间Tw的PDF为fi-x+1（t）。如图3所示，

任务i的fi-x+1（t）表示执行完前面i-x+1个任务所花费的时间。显然， Tw服从Erlang分布。 fi-x+1（t）的计算公式为：

fi-x+1（t）=（μxt）i-x（i-x）！ μx·e-μxt; t≥0，x

（16）

现在，已经求得（1-Ptimeout），将ηe和（1-Ptimeout）代入式（6），即可求得δ（x）。

3.3 SP关联指标

依据本文对安全性的定义：一方面，安全指标Na（x，n）反映了安全因素对可用VM数量的影响;另一方面，性能指标δ（x）反映了可用VM数量对服务性能的影响。

因此，可以通过将Na（x，n）与δ（x）组合来评估安全因素对服务性能的影响。 因此，定义SP关联指标来反映这种影响。E（δ（x））被定义为SP关联指标，它代表将安全性影响因素加入考虑的新的性能指标。根据贝叶斯方法，E（δ（x））的计算公式为：

E（δ（x））=∑nx=1Na（x，n）×δ（x）

（17）

可用VM的数量（x）在CCS中是不确定的，x可以等于1和n之间的任何数字，且取值概率为Na（x，n）。因此，E（δ（x））是通过对所有这些概率求和得到的。实验部分给出了计算该指标的仿真实例。

4 实验及分析

实验部分，首先采用仿真实例对建模方法进行验证，仿真在矩阵实验室（Matlab）上进行，其中将使用仿真程序计算的仿真结果与使用建模方法计算的理论结果进行比较。随后，进行了不同强度的安全机制对服务性能的影响的对比实验。最后，根据仿真结果，提出了三个关于在保持一定程度安全性的同时如何有效提高服务性能的优化建议。

4.1 建模方法的验证

表1～4显示了安全性建模方法和性能建模方法的参数配置。

如前所述，安全建模中，选用参数训练方法来获得P和hi，因此，直接在表1中指定了Pa的值。值得注意的是，有众多参数训练方法已经被大量应用，在这里就不具体介绍参数训练方法的细节。在表2中，根据文献[10]中的参数定义对f-dj进行了赋值。实际上，在真实环境中获得安全机制的CPU占用率是容易的。例如，现有操作系统都提供了检测每个运行的应用程序的CPU占用率的服务。在表3中，未分配参数x的值，因为，它的值取决于n的值。文献[9]表明安全性和服务性能是成反比的。因此，定义了表4中的参数取值，以满足安全性和服务性能之间的相关性。

下面对仿真程序的设定进行简要介绍：

1）仿真程序中μ以0.1为取值间隔从0.5到2.6进行取值。

2）所有4个VM都采用高强度安全机制。

3）仿真程序执行50×21次。在每次迭代中，定义循环1-000次的主循环结构。在仿真中，一个循环意味着理论建模方法中的一个单位时间。 50×21次迭代将产生50×21输出，其中：50表示μ的每个取值会产生50个结果;21表示μ有21个不同的值。这些输出中的每一个表示在不同μ值的任务的完成率。

4）假设每个任务可以在一个循环（一个单位时间）内完成。

5）如果VM处于吸收状态F，则在hF单位时间之后它将从F变为G。hF的取值如表1所示。

6）仿真程序运行中记录每项任务的信息，包括已到达、已完成和已放弃任务的数量。

7）设置随机数生成器。在仿真中，已经预定义了概率（VM的可用概率）以决定每个VM的可用性。在每个循环中，通过将预定概率与随机数进行比较来确定每个VM的可用性。

8）依据λ的值，设定仿真程序中确定每单位时间新到达任务的数量。

μ、 f-dj，以及可用VM的数量共同决定每单位时间完成的任务的数量。

比较结果如图4所示。 在图4中，理论结果与仿真结果完全匹配，服务速率增加。 该结果说明了所提出的安全性性能建模方法的正确性。

4.2 不同参数取值情况下的性能分析

选取三个主要参数，包括VM的数量（n）、安全机制的CPU占用率（f-dj）和VM的服务速率（μ），通过改变它们的取值来揭示它们对服务性能的影响。为了反映安全机制（f-dj）的CPU占用率对服务性能的影响，

在此设计了组1、组2和组3三个比较组，分别采用低、中和高强度安全机制。

如前所述，每个组由相同数量且采用相同强度安全机制的VM组成。

实验研究μ和n两个参数对服务性能的影响。μ值如下：

1）对于n，其取值范围为3到8。在本实验中，服务速率为μ=1.0s-1。结果如图5所示。

2）对于μ，为其设计了一组值。 μ的第一组值在0.6～1.8，到达率λ=2.1s-1。结果如图6所示。

3）不同安全机制的CPU占用率值（ f-dj），与表2中的相同。

4）其他参数的取值与表1、3～4中的相同。

实验的结果分析如下：

1）当可用资源，包括VM服务速率（μ）和VM数量（n）数量受到限制时，服务性能和安全性之間存在逆相关。例如，当图6中的μ=0.6～1.0或图5中的n=3～4时，低强度安全机制的E（δ（x））值（蓝线，组1）大于对于中等强度安全机制（黑线，组2）和高强度安全机制（红线，组3）的E（δ（x））值。这些结果表明，高安全性并不总是最佳选择。

2）随着可用资源的增加，服务性能与安全性之间存在正相关关系。如图5所示，高强度安全机制（红线）和中强度安全机制（黑线）的E（δ（x））值的增加率比大于低强度安全机制（蓝线）的E（δ（x））值的增加率比。

3）采取冗余備份策略是提高服务性能较好的策略。在图5中，E（δ（x））的值随着VM数量（n）的增加而迅速增加。

总的来说，上面两个实验说明了安全性对服务性能的影响，反映了恶意攻击和安全机制这两个安全因素是通过影响虚拟机的服务速率和可用虚拟机的数量来影响服务性能的。 因此，通过实验可知，安全性是服务性能评估不可或缺的因素。

5 结语

针对云环境缺乏安全性评估这一问题，本文提出了用分层建模方法和定义安全性性能关联指标来研究安全性（恶意攻击和安全机制）对服务性能的影响。所提出的建模方法通过两个关键因素（VM的数量和服务速率）建立了安全性和服务性能之间的连接。实验结果验证了所提出的建模方法的正确性，还获得了如下结论：1）当CCS面临严重的安全问题时，冗余是提高服务性能最简单、最可行的方法。 2）高安全性并不总是最佳选择。 3）当资源量有限时，服务性能和安全性之间是反相关的;当资源量充足时，服务性能和安全性之间是正相关的。未来可以将该建模方法进一步应用到调度算法的设计中去，以提升系统的服务性能。

参考文献（References）

[1] GONZALES D， KAPLAN J M， SALTZMAN E， et al. Cloudtrust — a security assessment model for Infrastructure as a Service （IaaS） clouds[J]. IEEE Transactions on Cloud Computing， 2017， 5（3）： 523-536.

[2]LIU L， WANG A， ZANG W， et al. Shuffler： mitigate crossVM sidechannel attacks via hypervisor scheduling[C]// Proceedings of the 2018 International Conference on Security and Privacy in Communication Systems， LNICST 254. Berlin： Springer， 2018： 491-511.

[3]SCHWARTZ M J. New virtualization vulnerability allows escape to hypervisor attacks[J]. Information Week Security， 2012， 4（2013）： 12.

[4]SINGH N， SINGH A K. SQLinjection vulnerabilities resolving using valid security tool in cloud[J]. Pertanika Journal of Science & Technology， 2019， 27（1）：159-174.

[5]LI P， LI J， HUANG Z， et al. Privacypreserving outsourced classification in cloud computing[J]. Cluster Computing， 2018， 21（1）： 277-286. [6]HWANG K， BAI X， SHI Y， et al. Cloud performance modeling with benchmark evaluation of elastic scaling strategies[J]. IEEE Transactions on Parallel and Distributed Systems， 2016， 27（1）： 130-143.

[7]CAO J， HWANG K， LI K， et al. Optimal multiserver configuration for profit maximization in cloud computing[J]. IEEE Transactions On Parallel and Distributed Systems， 2013， 24（6）： 1087-1096.

[8]HWANG K， SHI Y， BAI X. Scaleout vs. scaleup techniques for cloud performance and productivity[C]// Proceedings of the 2014 IEEE 6th International Conference on Cloud Computing Technology and Science. Piscataway：IEEE， 2014： 763-768.

[9]ZAMAN S， ADAMS B， HASSAN A E. Security versus performance bugs： a case study on FireFox[C]// Proceedings of the 8th Working Conference on Mining Software Repositories. New York：ACM， 2011： 93-102.

[10]BATISTA B G， FERREIRA C H G， SEGURA D C M， et al. A QoSdriven approach for cloud computing addressing attributes of performance and security[J]. Future Generation Computer Systems， 2017， 68： 260-274.

[11]ALIA M， LACOSTE M， HE R， et al. Putting together QoS and security in autonomic pervasive systems[C]// Proceedings of the 6th ACM Workshop on QoS and Security for Wireless and Mobile Networks. New York：ACM， 2010： 19-28.

[12]WANG Y， LIN C， LI Q. Performance analysis of email systems under three types of attacks[J]. Performance Evaluation， 2010， 67（6）： 485-499.

[13]LOMBARDI F， DI PIETRO R. Secure virtualization for cloud computing[J]. Journal of Network and Computer Applications， 2011， 34（4）： 1113-1122.

[14]ARSHAD J， TOWNEND P， XU J. Quantification of security for compute intensive workloads in clouds[C]// Proceedings of the 15th International Conference on Parallel and Distributed Systems. Piscstaway： IEEE， 2009： 479-486.

[15]OZKAN S. CVE details： the ultimate security vulnerabiltiy data source[EB/OL]. [2018-09-10]. https：//www.cvedetails.com/cve/CVE-2007-4593/

[16]KREIDL O P. Analysis of a Markov decision process model for intrusion tolerance[C]// Proceedings of the 2010 International Conference on Dependable Systems and Networks Workshops （DSNW）. Piscstaway：IEEE， 2010： 156-161.

[17]MADAN B B， GOGEVAPOPSTOJANOVA K， VAIDYANATHAN K， et al. Modeling and quantification of security attributes of software systems[C]// Proceedings of the 2002 International Conference on Dependable Systems and Networks. Piscstaway： IEEE， 2002： 505-514.

[18]XU F， LIU F， JIN H. Heterogeneity and interferenceaware virtual machine provisioning for predictable performance in the cloud[J]. IEEE Transactions on Computers， 2016， 65（8）： 2470-2483.

[19]ZHU Z， DONG S， YU C. A text hybrid clustering algorithm based on HowNet semantics[J]. Key Engineering Materials， 2011，474/475/476：2071-2078.

This work is partially supported by the National Natural Science Foundation of China （61602094）.

XU Han， born in 1990， Ph. D. candidate. His research interests include cloud computing， system modeling.

LUO Liang， born in 1980， Ph. D.， lecturer. Her research interests include cloud computing， energy modeling， system modeling.

SUN Peng， born in 1979， Ph. D.， lecturer. Her research interests include cloud computing， autonomic computing， intelligent scheduling.

MENG Sa， born in 1987， Ph. D. candidate. His research interests include cloud computing， resource scheduling.