基于Abaqus 的超声波A 扫法的仿真实验验证
2019-12-23顾继俊
刘 松,顾继俊
(中国石油大学(北京),北京 102200)
0 引言
随着近代工业领域的快速发展,无损检测作为一种快速、高效的缺陷检测技术,普遍应用于工业检测当中[1]。超声波检测是无损检测中常用的方法之一,其优势是在不改变检测对象的物理性质的前提下,能够利用检测物体与缺陷在声波传播上性能的差异,根据声波的反射情况和能量变化,对检测对象的内部及表面结构进行分析和检查。超声波检测扫查的方式很多,包括A 扫、B 扫、C 扫、S 扫等,每种方法都具有各自的特点及优势。超声波A 扫法是最早被提出的,最简单、最普遍的缺陷定位方法[2-3]。
由于超声波检测结果不受检测物内液体的影响,所以超声波检测方法在液体容器检测中应用广泛[4]。针对石油储罐底板的损伤缺陷识别,应用Abaqus 有限元软件对储罐底板进行超声波A 扫法仿真分析,对缺陷进行定位识别,将结果与实际情况进行对比,验证其正确性[5-8]。
1 仿真模型建立
1.1 仿真框架
在进行仿真之前需要确立仿真框架,计算求解所需要的参数,提高仿真效率和准确性。仿真求解包括前处理、求解计算、后处理(图1)。
1.2 材料和基本参数的确定
检测试件为石油储罐底板,材质为Q235 钢板,具体参数选择如下:探头选用500 kHz 的双晶探头,实现一发一收功能,材料为Q235 钢,尺寸为300 mm×300 mm×16 mm,杨氏模量为2.10E11 Pa,泊松比为0.3,密度为7800 kg/m3,缺陷是在钢板正中心的一个正方形,尺寸为10 mm×10 mm×5 mm,位置如图2 所示。
1.3 脉冲函数的选择
应用Abaqus 有限元软件模拟超声波,是通过施加位移约束来模拟应力应变效果的,即施加位移约束模拟超声波。普通的正弦信号或者方波信号,在钢板中传播后,很难辨别,对分析带来困难。选取用Matlab 的HANNING 窗函数调制信号来激励超声波[9-10],表达式见式(1)。

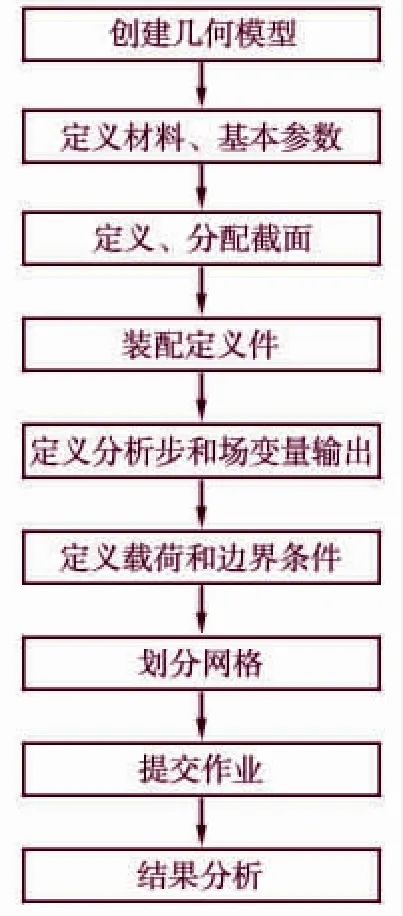
图1 Abaqus 仿真流程
其中,x(t)为振幅,fc为中心频率,n 为激励信号函数中波形的个数。
图3 为中心频率为fc=500 kHz、周期n=4 的HANNING 窗函数调制信号。
1.4 载荷时间步的选取
在有限元法计算中,选取适当的载荷时间步Δt 对计算结果的准确性非常重要。虽然Δt 越小,结果越精确,但是对计算机性能要求太高,计算时间越长,一般来讲时间步到达以下方程就可以达到要求。

其中,fmax为探头的最大频率。在本仿真中,时间步取1E-7 s。
1.5 计算时间的选取
计算时间的选取十分重要:时间太长则浪费时间,还会导致分析文件过于庞大;时间太短,则探头接收不到回波。
超声波在一般情况下,纵波在Q235 钢中的传播速度大约为5900 m/s,但由于超声波缺陷检测中,声速的误差会导致缺陷位置的较大误差,所以要先进行无缺陷试件检测,求出准确声速VC。
在无缺陷试件中,波速VC可取5900 m/s 来计算大致计算时间。为了方便计算,取计算时间为1.5E-4 s。
1.6 网格大小
与载荷时间步Δt的选择一样,网格大小也十分重要。网格越小,计算准确性越高,但对于计算机要求也更高。查阅资料可知,网格大小只要小于1/10 波长就能达到要求。为了方便,取网格大小为1 mm 计算。
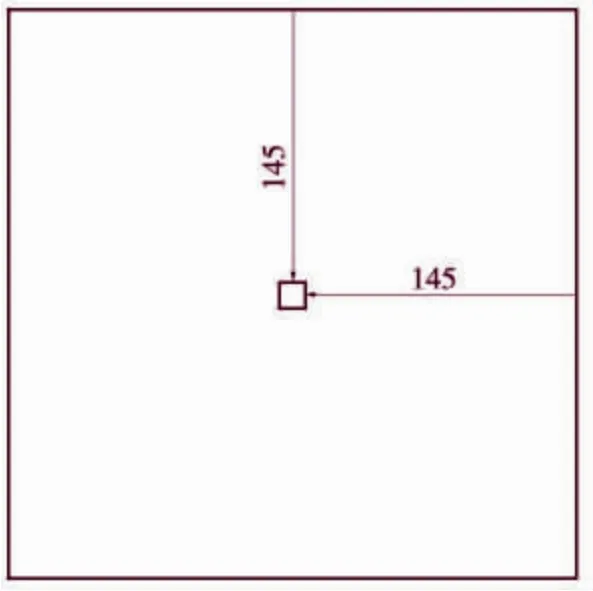
图2 缺陷位置示意

图3 HANNING 窗函数调制信号
网格尺寸方程如下:

其中,l 为网格尺寸,λmin为最小波长,VC为波速,fmax为探头最大频率。

图4 声波在钢板内的传播过程
2 仿真分析
2.1 超声波在无缺陷板内的传播过程
在进行缺陷的定位识别之前,先进行了同样的无缺陷钢板的超声波仿真,求出波速VC。为了减少计算时间,选取模型的上表面使用三维壳单元进行模拟。提交作业后,观察声波在钢板内的传播过程云图(图4)。
为了避免声波端面反射影响,取距上端面1 网格(1 mm)距离的节点和距底面1 网格距离的节点的振动状态进行分析,求解波速。节点位置如图5 所示,X-Y 图中两点坐标峰值如图6、图7 所示。

图5 提取坐标节点位置
2.2 波速VC 的计算
根据X-Y 图节点坐标,可以计算波速VC,方程如式(5)所示。
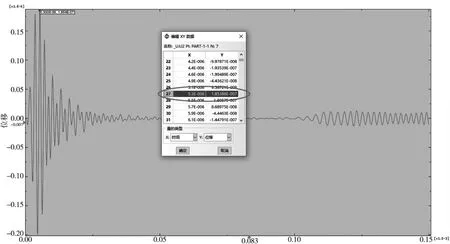
图6 上节点峰值坐标X-Y

其中,VC为波速,Δt 为声波在上下节点时间差,l 为上下节点的距离。

结果接近理论波速5900 m/s,具有一定准确性。
2.3 缺陷定位
参数设置与无缺陷仿真一,时间取上述上节点为参考点,进行振动状态分析。得到的缺陷数据X-Y 图如图8 所示。
图7 中,方框内的信号就是缺陷所反射的信号,上节点的峰值时间为5.374E-6 s,缺陷除峰值时间为5.578E-5 s,在无缺陷仿真中确定的波速为5876 m/s,由此可以求得缺陷位置。

其中,L 为上节点到缺陷的距离,T 为缺陷的峰值时间,t 为上节点峰值时间。
通过上式可求得L=145.82 mm,上节点与缺陷上边缘实际距离为144 mm,正确率为×100%=1.26%,可见结果的可靠性较高。
3 结论
应用Abaqus 数值模拟软件进行了超声波A 扫法缺陷检测的仿真实验,对有无缺陷的两种储罐底板进行了超声波检测,确定了波速并对缺陷进行了定位且误差仅为1.26%,验证了超声波A 扫法进行固体底板缺陷定位的可行性。

图7 下节点峰值坐标X-Y

图8 缺陷数据X-Y
