球载雷达多杂波自适应抑制
2019-12-23宿文涛刘润华张小涵
宿文涛,汪 枫,刘润华,张小涵
(空军预警学院, 湖北 武汉 430019)
0 引 言
近年来,球载雷达以预警能力强、低空性能好、留空时间长和效费比高等优势,越来越受到世界各国军队的青睐[1-2]。面对低空、超低空突防的威胁,球载雷达是有效的抵抗手段之一。而球载雷达检测这些目标存在两个主要难点:一是面临的杂波环境与常规雷达有所区别[3],波束俯视导致杂波强度大,雷达平台的移动使固定的地杂波频谱发生移动和展宽,难以确切知道杂波的频谱特征[4]。二是低空低速目标受到强大的地杂波的干扰[5],由于速度较慢,其特性在多普勒域与杂波非常接近,导致传统的频域滤波方法难以处理。
对于低空低速目标的检测,能否精准的去除杂波,保留低速目标是关键。这就要求滤波器的阻带要与杂波的频谱展宽相匹配,通带要尽可能的平坦以保留目标信息。传统的延迟线对消器是现役球载雷达采用的滤波方法,虽然延迟线对消器的改善因子随对消脉冲数的提升而提升,但是其阻带的宽度以及通带的平坦度是不可控的,这就限制其对低空低速目标的检测性能。
针对上述问题,本文采用改进的特征矢量法设计滤波器来匹配杂波频谱特征,使用相关函数法来估计频谱特征,针对估计误差过大的问题运用覆盖法尽可能消除误差的影响。通过计算机仿真,验证了方法的有效性。
1 杂波模型
球载雷达接收的回波信号中可能包含地物、海浪以及云雨等多种杂波。雷达位于陆地上空时主要是地物和云雨杂波,位于海面上空时主要是海杂波[6]和云雨杂波。球载雷达面临的杂波一般均可以用高斯模型表示[7],对于多个杂波来说其归一化形式为
(1)
式中:fdk为第k个杂波的中心频率;σck为第k个杂波的标准差,代表频谱的展宽程度。
(2)
式中:vk为第k个杂波的相对水平速度;ψ为俯视角;λ为雷达波长。
(3)
例如波长为0.3 m,重复频率为300 Hz,天线转速为6 r/min,θ3=2°时,表1给出了一般情况下几种杂波谱的典型谱宽。

表1 几种典型杂波的标准差
根据维纳滤波理论,杂波的自相关函数与功率谱密度互为傅里叶变换,因而杂波的自相关函数可以表示为
Rc(i,j)=F-1[S(f)]=
(4)
令τij=ti-tj为相关时间,将(1)式带入(4)式化简得
Rc(i,j)=
(5)
由式(5)可以看出,多个高斯谱的混合杂波,其自相关函数由对应的多杂波分量之和构成。由随机过程相关理论可知,平稳随机过程的自相关函数就是它的协方差矩阵。因此,由Rc(i,j)构成的多杂波协方差矩阵为
(6)
2 基于特征矢量法的实时处理技术
滤波器的设计目标就是设计一组合适的滤波器系数,使其有效地抑制杂波,并保证目标信号能无损失地通过。滤波器的输出[9]为
y(t)=wTx(t)=w(i)x(t-iTr)
(7)
式中:w=(w0,w1,…wN)T为权矢量,x(t)为信号矢量,Tr为球载雷达的脉冲重复周期。工程上常以改善因子来衡量权系数的性能优劣。改善因子定义为I=(So/Co)/(Si/Ci),显然,改善因子越大,其对杂波的抑制效果越好。
用特征适量法设计的滤波器对多个杂波组成的混合杂波有较好的滤波效果[10]。特征矢量法是以平均改善因子最大为准则的杂波抑制方法。它属于有限脉冲响应(FIR)滤波器的一种,其系统函数为
(8)
式中:N为滤波器阶数。
已经证明[11-12],要使改善因子达到最大,滤波器的最佳权矢量应为输入杂波的协方差矩阵Rc的最小特征值λmin对应的特征向量。
Rcwopt=λminwopt
(9)
此时,平均改善因子达到最大。
(10)
由式(9)可知,由特征矢量法计算滤波器系数w取决于杂波协方差矩阵Rc,由式(5)、式(6)可知Rc由fdk和σck所决定,所以最佳权系数w是fdk和σck的二元多维复函数矢量,记为w(fdk,σck)。
如果已知滤波器的权系数,则特征矢量法构造的滤波器的频率响应函数与其它FIR滤波器类似,可以统一由式(11)表示:
(11)
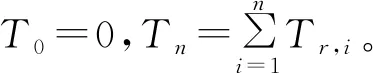
雷达脉冲重复频率300 Hz时特征矢量法滤波器的频率响应如下图。为了便于阐述,不失一般性,本文以两个杂波(地杂波和云雨杂波)为例阐述多杂波自适应抑制。

表2 仿真参数设置
经计算其中各权矢量数值如下:
w3=[-0.60+0.06i,0.27+0.51i,0.61]
w4=[0.38+0.14i,0.47-0.32i,
0.34-0.46i,-0.41]
w5=[-0.15-0.20i,-0.53-0.05i,
-0.24+0.50i,0.37+0.39,0.26]
wg=[-0.27+0.24i,-0.56+0.22i,
0.27+0.54,0.36]
由图1、图2可知特征矢量法设计的滤波器的凹口位置和宽度都随杂波的数量和谱宽的变化而自适应变化。这样的特性比较适合用于球载雷达面临的多个不同杂波的情形。但是特征矢量法构造的滤波器处理多个谱宽不同的杂波时性能会有不同程度的恶化,滤波器阶数较少时,特征矢量法求解的零点较少,分辨率不高导致两个凹口宽度近似相等,滤波器阶数较多时凹口较浅且宽度较大。因此要对该方法进行改进以适应多个不同频谱特征的杂波抑制。
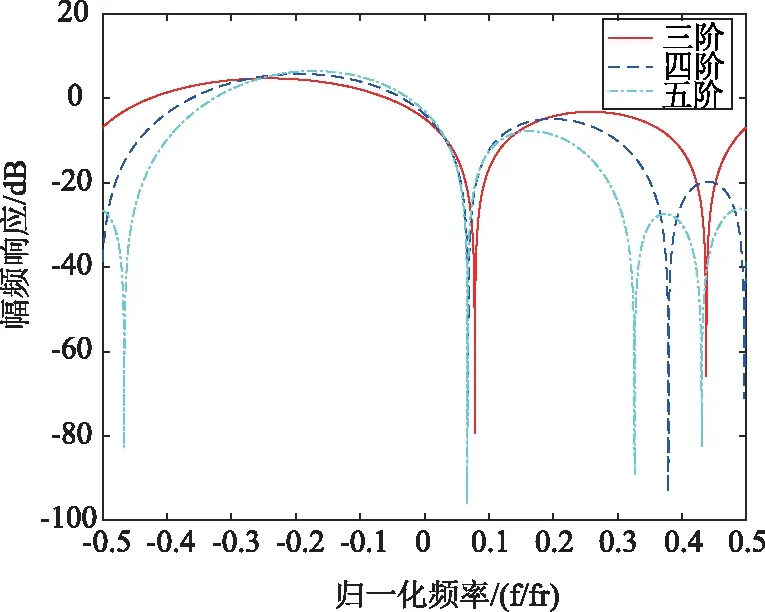
图1 多凹口幅频响应 (谱宽不同时)

图2 改进滤波器幅频响应
针对该方法在抑制多个具有不同频谱特性杂波时性能恶化的问题,可以采用设置虚拟杂波的方式来增加谱宽。由图1可知特征矢量法处理谱宽相同的多个杂波性能较好,所以首先选择谱宽较窄的地杂波的谱宽为参考作为其它所有杂波的谱宽值,然后在谱宽较宽的云雨杂波的频率附近设置合适的虚拟杂波来增加云雨杂波处的阻带宽度。例如地杂波谱中心20 Hz、谱宽2 Hz,云雨杂波谱中心130 Hz、谱宽20 Hz,生成滤波器系数时以谱中心分别为20 Hz、130 Hz、125 Hz(虚拟设置的杂波),它们的谱宽均为2 Hz,这样虚拟设置的杂波(fd=125 Hz,σc=2 Hz)就起到了拓宽云雨杂波谱宽的作用。效果如图2所示,虚拟杂波设置示意如图3所示。注意滤波器的阶数应大于总的杂波数(真实杂波加虚拟设置的杂波)

图3 虚拟杂波设置示意图
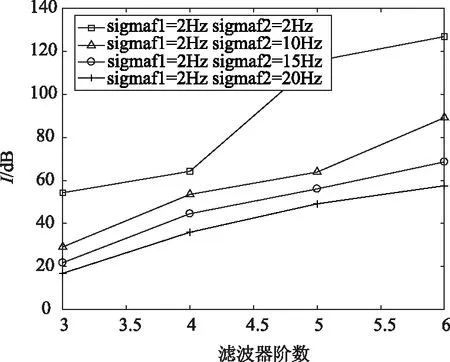
图4 特征矢量法处理多杂波时的改善因子

图5 改善因子对比
由图4清晰地可以看出特征矢量法处理两个频谱特征存在差异的情况下性能会恶化,且差异越大,性能恶化越严重。由图5可以看出本文对特征矢量法的改进明显会提高改善因子,性能的改善与设置的杂波的位置有关,但是改善效果不会超过特征矢量法处理两个谱宽相同的杂波的改善因子值。
3 杂波特征提取
要实现自适应杂波抑制需要提取杂波频谱特征(杂波中心频率和杂波谱宽)来计算滤波器系数。传统的自适应滤波通常采用两级级联的滤波器:地杂波(零多普勒频移)滤波器和运动杂波(海杂波或云雨杂波)滤波器,这种情况下通常只能估计一种杂波的频谱特征,因此需要先通过地杂波滤波器滤除地杂波,以减少地杂波对运动杂波估计的影响。本文第一节已提到球载雷达的地杂波并不是固定的,随着平台的移动会展现类似运动杂波的特性,因此对球载雷达杂波而言,需要同时提取包括地杂波在内的多个杂波的频谱特征。由式(5)可知,杂波的频谱特性由谱宽σc和功率谱中心fd决定。对于确定的σc和fd基于特征矢量法的滤波器权矢量也就确定了。对于球载雷达检测低空低速目标而言,由于目标与杂波频谱特征相近,所以杂波特征估计的准确性,决定了检测的性能。
因此,有必要采取方法同时对多个杂波的频谱特征进行估计,同时也要采取措施尽可能减少估计误差。使用相关函数法[13-14]可以估计多个杂波的特征,注意进行多杂波特征同时估计时,需要满足多个杂波在不同距离,即在距离上杂波不重合。
多杂波可表示为如下形式:
(12)
式中A(t)为复包络;Tk为第k个杂波存在范围对应的时间宽度;fdk为第k个杂波的多普勒频率;φ0为初相;n(t)为加性白噪声。延迟一个周期可写成:
u(t-Tr)=
(j2πfdk(t-Tr)+φ0)+n(t-Tr)
(13)
一般情况下,噪声与杂波不相关,注意到各杂波之间由于时间上不同也均不相关,所以它们的相关函数为:
R(Tr)=E[u(t)u*(t-Tr)]=
(14)
式中B(Tr)=E[A(t)A(t-Tr)]。A(t)为窄带信号,即A(t)=A(t-Tr),那么B(Tr)=E[|A(t)|2]为一实数。由式(14)可得
(15)
对一般遍历平稳随机过程可由时间平均代替统计平均,得到估计式
(16)
式中i表示杂波在不同脉冲上的独立采样序列号。结合(15)(16)式得到杂波的多普勒频率估计值
(17)
假设地杂波位于5~15 km处,谱中心为65 Hz,谱宽为11 Hz,云雨杂波位于25~80 km处,谱中心为130 Hz,谱宽为26 Hz,用相关函数法进行估计,结果如图6所示。

图6 相关函数法估计结果
由图6可以看出利用相关函数法对杂波进行估计,频率估计在相邻单元有一定的差距,但均在预设值上下波动,也即存在一定的谱宽。取邻近单元的测频值求平均作为谱中心估计值,标准差作为谱宽估计值。表3给出了相关函数法估计多杂波谱宽谱中心的仿真统计结果。
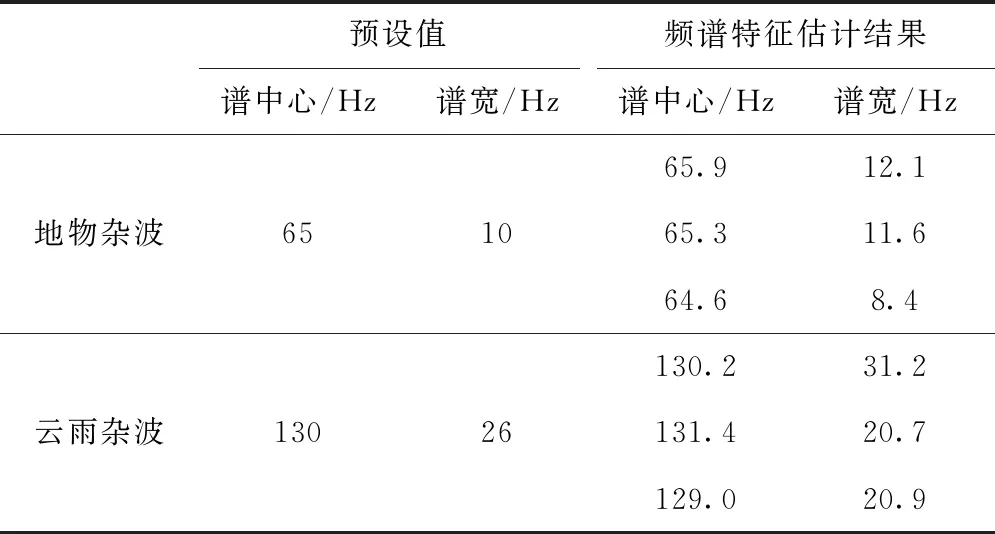
表3 相关函数法频谱估计结果
由表3的结果可知,相邻函数法的谱中心估计效果较为理想,但是谱宽估计有很大误差地杂波谱宽预设值为10 Hz,估计值为8.4~12.1 Hz,误差为-1.6~2.1 Hz。而云雨杂波谱宽预设值为26 Hz,估计值为20.7~31.2 Hz,误差为-5.3~5.2 Hz,相对误差较大且可能偏大也可能偏小,这也是大多数频谱估计方法的共性。
4 球载雷达多杂波自适应抑制
4.1 谱宽覆盖法
考虑到谱宽σck的估计误差太大,这对低速小目标的检测是不能容忍的。因此要尽可能地减小误差带来的影响。在陆地上空球载雷达主要面临地杂波和云雨杂波的干扰,由前面分析可知地杂波的综合谱宽较窄一般为10 Hz左右,估计误差在±2 Hz左右,云雨杂波的谱宽则一般为26 Hz左右,估计误差在±5 Hz左右,可以看出谱宽越大,误差越大。
设相对误差
(18)
地杂波的相对误差δσc=0.19,云雨杂波的相对误差为δσc=0.25,因此可以在谱宽估计的基础上,对谱宽的取值进行量化拓展,形成多组滤波器同时进行滤波。谱宽的量化拓展与第二节对特征矢量法的改进是匹配的,通过设置虚拟杂波的形式实现。各个杂波的谱宽差异很大,理论上,地杂波的谱宽最小,云雨杂波的谱宽较大一般是地杂波的1~3倍,箔条等其他杂波一般是地杂波的1~2倍。因此选择地杂波的频谱特征值作为参考值。频宽覆盖法的步骤:
(2)设置虚拟零点拓宽其他杂波的谱宽,设步进频率Δfd=σc1/4,以云雨杂波fd2为例,考虑到计算量,在fd2左右各设置一个虚拟杂波,共设置三组fd2±2Δfd、fd2±3Δfd、fd2±4Δfd,三组虚拟杂波的设置对应形成三组谱宽不同的滤波器,这就对杂波谱宽进行了覆盖,很有可能将谱宽的真值包含在内。虚拟杂波的个数和频宽覆盖的组数可以灵活设置,在这里考虑到计算量,设置的组数较少。依据前面所述,这三组可以求出三个滤波器系数。如某一种情况下的滤波器的频率响应如图7所示。

图7 多组滤波器频率响应
4.2 系统组成
针对多杂波同时抑制问题,采用特征矢量法求解权系数,自适应杂波抑制需要估计多个杂波频谱特征,由于估计谱宽存在较大误差,该系统运用频宽覆盖法尽可能减小估计误差的影响。系统组成如图8所示。

图8 系统组成框图
系统由杂波存储单元、杂波特征估计、权系数求解及扩展权系数、多组滤波器和一个比较器组成。
具体步骤如下所示:
(1)在本系统中,首先对杂波进行N个脉冲采样得到ui(t),i=1,2,…N并进行存储。

(3)考虑到谱宽σck的估计误差太大,利用频宽覆盖法形成多组滤波器,然后将杂波数据并行输入到滤波器中,比较每一个滤波器的输出结果,以输出杂波剩余最小的滤波器作为最佳输出。
5 仿真分析
为验证多杂波抑制方法的有效性,分别对特征矢量法,改进特征矢量法杂波抑制性能进行对比分析。
球载雷达高度H=3000 m;脉冲重复频率fr=3000 Hz;载频f0=3 GHz;天线俯仰波束宽度θ3=10°;天线水平波束宽度φ3=1.8°;设置为球载雷达平台速度为vr=5 m/s,云雨杂波速度vc=15 m/s,对应地杂波多普勒频率与云雨杂波多普勒频率分别为100 Hz与300 Hz,其中地杂波的谱宽为设置为10 Hz,云雨杂波谱宽为30Hz。在5 km处设置一目标,目标的高度为500 m,速度为10 m/s,对应多普勒频率为200 Hz,平均信杂比为设置为-10 dB。
图9为滤波前杂波功率谱示意图,图9(a)可以看到地杂波与云雨杂波,由于目标功率小于地杂波,所以目标淹没于地杂波中无法分辨,图9(b)为目标所在距离单元的功率谱,可以看到目标基本位于杂波副瓣内,较难分辨。

图9 滤波前结果示意图
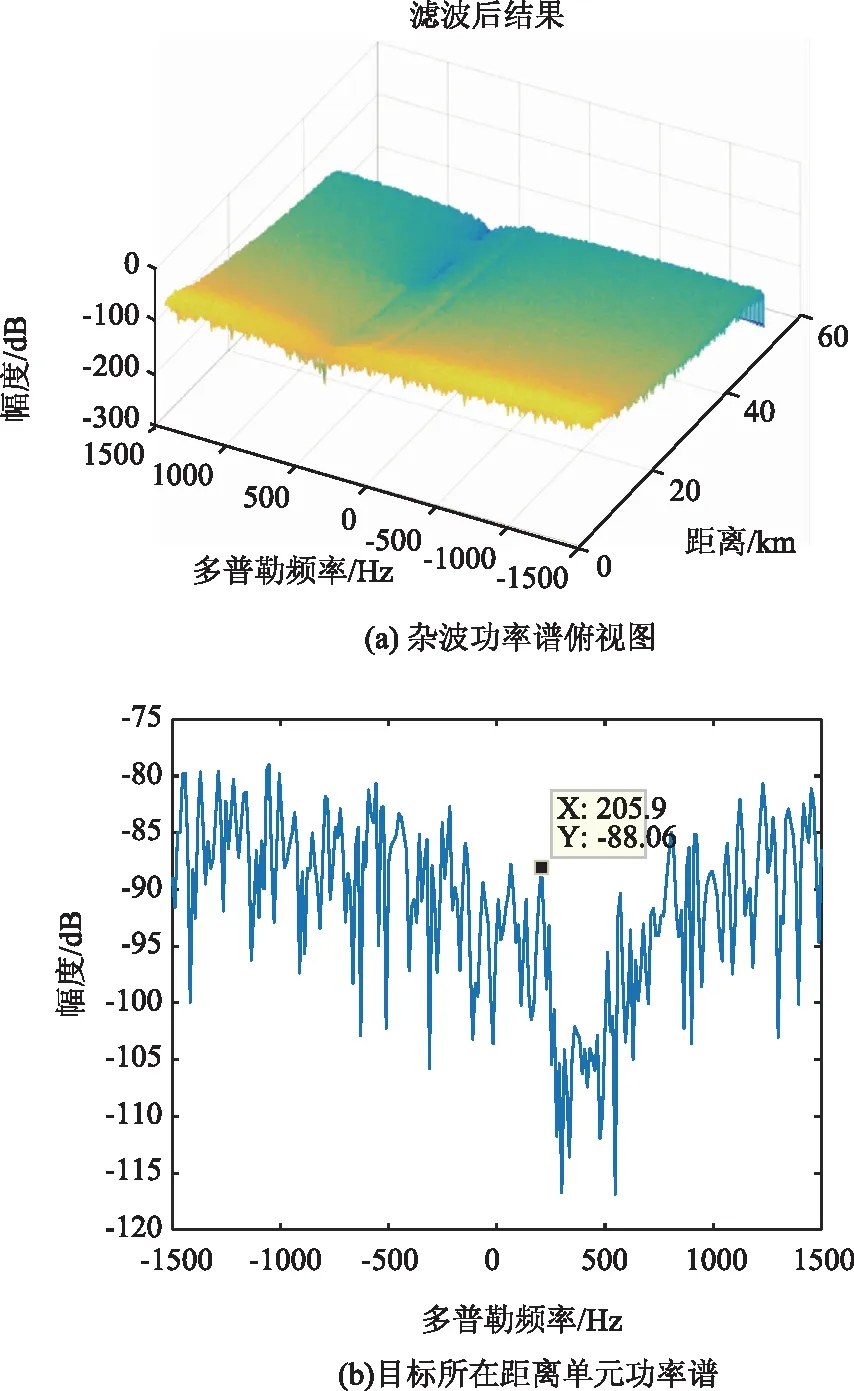
图10 特征矢量法滤波后结果示意图
图10是采用特征矢量法滤波后结果示意图,从图10(a),图10(b)均无法分辨目标信息,这是由于该方法处理多个不同杂波时性能恶化导致,在云雨杂波处形成了宽的凹口对目标也进行了削弱,导致信杂比的改善并不理想。
图11是采用改进的特征矢量法滤波后结果示意图,从图11(a)可以看到一点目标的信息,从图11(b)可以较为清晰地分辨目标信息。由前面分析已知,改进的特则矢量法可以较好的匹配杂波频率与谱宽,尽可能的保留目标信息,对信杂比改善的效果较好。

图11 改进特征矢量法滤波后结果示意图
6 结 语
球载雷达杂波环境的特殊性导致了传统的自适应杂波抑制方法不适应,本文分析了球载雷达杂波特性,针对多个杂波同时抑制的情况采用基于最大平均改善因子的特征矢量法计算滤波器系数,特征矢量法在处理多个频谱特性差异较大的情况下性能会恶化,提出了通过设置虚拟杂波的方法改善其性能,通过仿真验证其性能有较好的改善;基于相关函数法推导了多杂波频谱估计的相关理论,针对估计误差较大的问题,结合改进的特征矢量法具有可以自由设置虚拟杂波来拓展谱宽的特点,在杂波估计的谱中心附近形成多种谱宽覆盖。该系统比传统杂波抑制相比可以同时处理多个未知的杂波,且具备减小误差的优点。本文方法含义明确,计算也不复杂,可操作性强,对球载雷达具有较强的使用价值。
