移动低占空比传感网中时延感知的邻居发现算法
2019-12-23李文娟王宝珠杨浩澜
李文娟,王宝珠,杨浩澜
(1.重庆邮电大学移通学院,重庆 401520; 2.重庆邮电大学,重庆 400044)
0 引 言
作为新型自组织网络一样,移动低占空比无线传感网络(Mobile Low-Duty-Cycle Wireless Sensor Networks, MLDC-WSNs)与传统的无线传感网络(Wireless Sensor Networks, WSNs)[1]既有相同点,也有不同之处。相同点在于:它们都有海量、微型的、存储容量和计算能力有限的传感节点组成[2]。不同之处在于:MLDC-WSNs内的节点不仅可以移动,而且休眠时间长(即低占空比)[3-5]。
MLDC-WSNs使节点以低占空比状态保存节点能量。然而,低占空比技术虽然保存了节点能量,延长了网络寿命,但是其产生一个新的问题—以低占空比工作的节点如何发现邻居节点[6]。
在MLDC-WSNs中,传感节点多数时间保持休眠状态,这就可能出现原本两个物理邻居节点,却不能发现彼此现象,即它们并不知道彼此的存在。若再考虑传感节点的移动性,发现邻居节点更难度。
而邻居发现是构建网络拓扑的重要操作。网络内的节点需要快速地发现邻居,进而形成网络。由于网络内所有节点需要发现邻居,一个快速、低能耗的邻居发现策略能够提高网络性能,延长网络寿命[7-8]。而在MLDC-WSNs中,节点采用低占空比模式工作,并要求节点间同步唤醒。这就使得节点可能需要等待较长时间,邻居节点才唤醒。这增加了时延。
因此,如何以低时延、低功耗方式发现邻居成为MLDC-WSNs的研究热点。目前,现有的多数研究策略是让节点主动唤醒(actively wake up)去发现邻居。但是这种策略要求节点唤醒多次,增加了能量消耗。
为此,提出时延感知的邻居发现(Low-latency -Aware Neighbor Discovery, LAND)算法。LAND算法通过预测节点的移动距离,估计节点邻居集,并进行主动唤醒。仿真结果表明,提出的LAND算法有效地控制发现邻居的时延,并提高邻居发现率。
1 约束条件及问题描述
1.1 约束条件
令G={V,E}表示MLDC-WSNs网络,其中V表示n个传感节点的节点集,即V={s1,s2,…,sn}。而E表示节点是否与其他节点连通的信息。G内节点采用低占空比工作模式,如图1所示。节点在多数时隙内处于休眠,少数时隙处于唤醒。在唤醒状态时,节点可以发送数据和与其他节点通信。此外,节点可以在任何时隙主动唤醒,并发送数据包,但是,只能在预定的唤醒时隙内接收数据包。
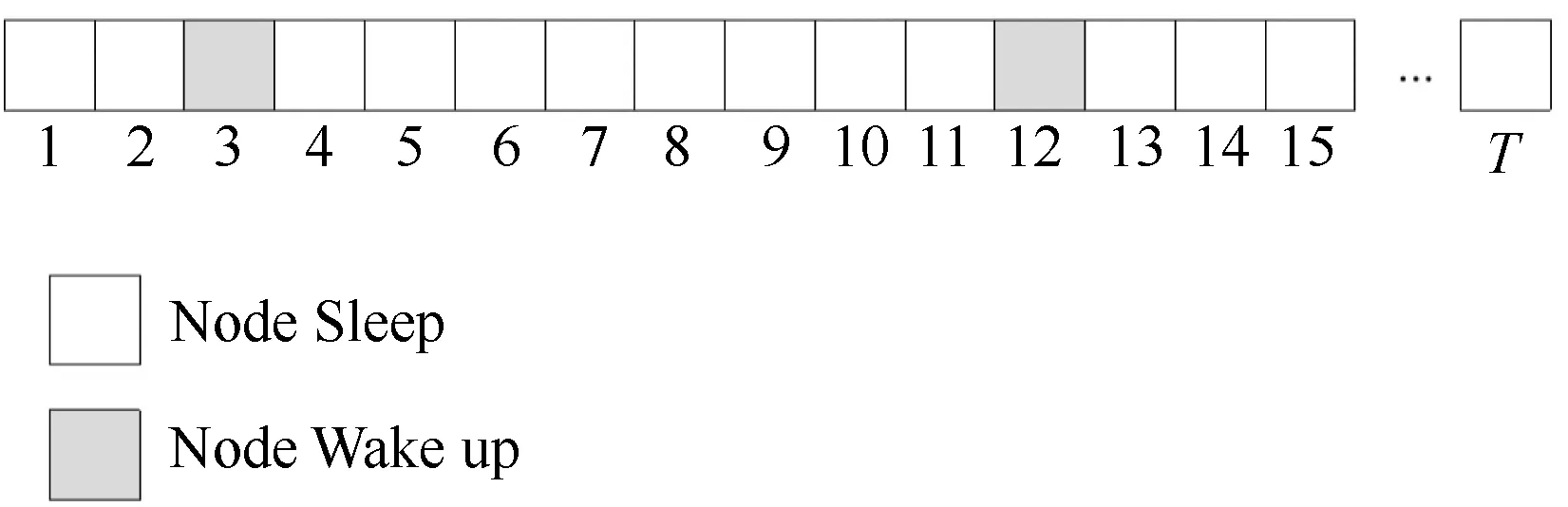
图1 节点的低占空模式
令R表示MLDC-WSNs内节点的通信半径。节点可以与其通信范围内的节点通信。此外,引用随机路点移动 (Random Waypoint Mobile, RWM)模型[9]。在RWM模型中,节点随机地选择移动方向,且在速度范围[0,ϑmax]内移动。在特定时间Δt内,节点可以移动的最大距离为Δt×ϑmax。
1.2 问题描述
假定节点si和节点sj在时间t可以相遇。节点在Δt内,它们在彼此通信范围内。它们均在Δt唤醒,且Δt不小于节点实施邻居发现的最小时间tmin(Δt≥tmin)。
基于上述假设,节点si和节点sj能够在[t,t+Δt]内发现邻居。令δ表示发现邻居的时延,其定义如式(1)所示:
δ=t+Δt-t0
(1)
其中t0表示两个节点能够相互通信的时刻。而t+Δt表示这两个节点完成相互发现的时刻。
令Pij表示节点si和节点sj在彼此通信范围内能够发现彼此的概率。若Pij(t)=0,则表示它们在t时间不能够发现彼此;若Pij(t)=1,则表示它们能够发现彼此。
令P(t)表示邻居发现率,且P(t)=m/N。其中m表示发现的邻居数,而N表示总的邻居数。因此,MLDC-WSNs中邻居发现问题可简述为:以最低的时延实现最大化的邻居发现率:
{minδ,maxP(t)}
(2)
2 LAND算法
LAND算法由有两个阶段构成。在第一阶段,节点依据网络部署,构建初始节点集;在第二阶段,节点有选择性地主动唤醒节点,并发现邻居。
2.1 第一阶段

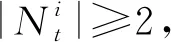
第一步:网络内每个节点在自己唤醒时隙内广播消息,通知网络,自己的存在。如图2所示,在时隙t0,节点si和节点sj在彼此通信范围内,能够接收彼此广播的消息。然后,它们交换休眠-唤醒时刻表(Sleep wake-up Timetable, SWT)信息。

图2 初始邻居节点的构建

一旦收到节点si的邻居信息,节点sj就在节点si的邻居节点(为节点sk)的唤醒时刻t3主动唤醒,并向节点sk发送确认信息ACK:节点sk是否能成为自己的邻居节点。如果节点sk收到ACK,则节点sk成为节点sj的邻居节点。即节点sj发现了新的邻居节点sk。
2.2 第二阶段
一旦构建了初始邻居集后,就进行第二阶段。第二阶段主要考虑节点的移动问题。即当有节点在节点si周围移动,节点si就主动唤醒,进而发现邻居节点。
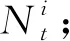

图3 节点移动
dix∈[0,R-ΔS)
(3)
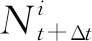
dix∈[R+ΔS,+∞)
(4)
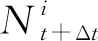
dix∈[R-ΔS,R-ΔS)
(5)
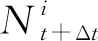
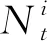
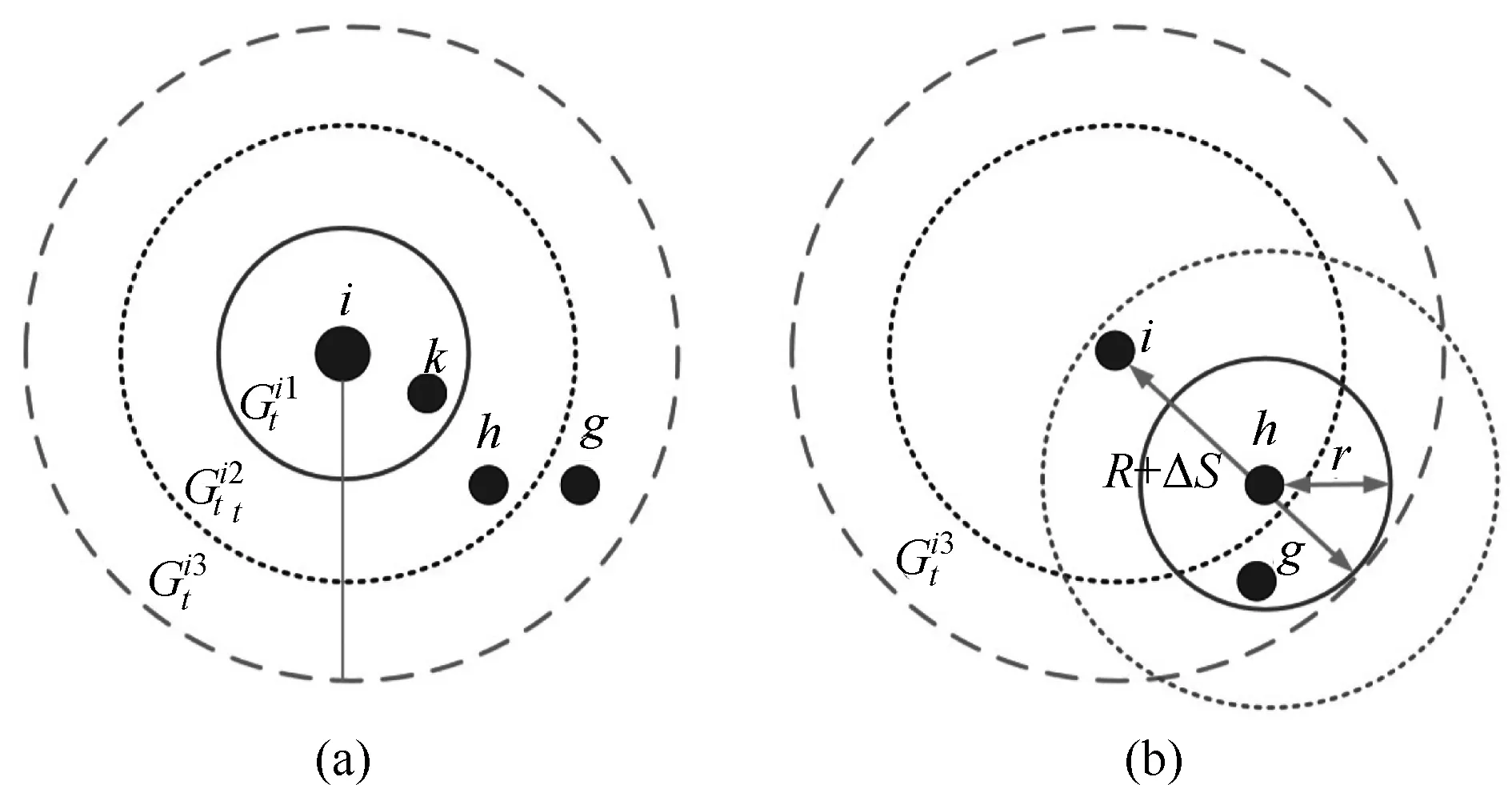
图4 节点邻居集

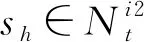
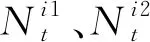
(6)
3 性能分析
3.1 仿真参数
利用MATLAB软件建立仿真平台。在1000 m×1000 m区域内随机部署500个低占空比节点。所有节点依据RWM模型在区域内移动。节点默认的移动速度为1 m/s,最大移动速度ϑmax=1.3 m/s。节点占空比为5%,这意味着每20个时隙只有一个时隙,节点保持唤醒状态。考虑T=5000个时隙节点,每个时隙时长为10 ms。节点默认的通信半径R=100 m。
此外,为了更好地分析LAND性能,选择文献[10]的Disco、文献[11]的CBD和文献[12]的Birthday作为参照,并分析它们的平均邻居发现时延、唤醒次数和节点邻居发现率。
3.2 发现邻居的平均时延
本次实验分析占空比和移动速度对平均时延的影响,如图5所示。

图5 发现邻居的平均时延
图5(a)显示了占空比对平均时延的影响,其中节点移动速度为1 m/s,占空比从1%~10%变化。从图可知,占空比的增加,降低了平均时延。相比于CBD和Disco算法相比,LAND算法的平均时延得到有效控制。例如,当占空比为0.05时,LAND算法的时延为10s, 而Disco和CBD算法的时延分别62 s和22 s。
图5(b)显示了移动速度对平均时延的影响,其中占空比为3%,节点移动速度从1m/s至10m/s变化。从图可知,平均时延随移动速度的加快而下降。原因在于:移动速度的加快,节点相遇的频率增加,这有利于发现邻居节点。相比于Disco和CBD算法,LAND算法的平均时延随移动速度变化波动小,且保持低的平均时延。
3.3 唤醒次数
本次实验分析节点在发现所有邻居节点所需的次数。图6显示Disco、CBD和LAND算法的唤醒次数随低占比的变化。

图6 唤醒次数随低占比的变化
从图6可知,唤醒次数随占空比的增加呈下降趋势。原因在于:占空比越高,节点唤醒的时隙数越高,就无需多数唤醒节点。此外,相比Disco和CBD算法,LAND算法有效地控制唤醒次数。例如,当占空比为0.07时,LAND算法的唤醒次数约为12,而Disco和CBD算法的唤醒次数达到约26和22,而Birthday算法的唤醒次数为约15。
3.4 节点邻居发现率
本次实验分析发现时延对邻居发现率的影响,其中低占比为0.05,移动速度为3 m/s。
从图7可知,当发现时延较低时,LAND算法和Birthday算法的发现率相近,它们能够快速地发现邻居。相比之下,Disco算法发现邻居节点速度较慢。当发现率增长一定量后,Birthday算法的发现率的增长速度放缓,而LAND算法的发现率仍能够维持快速地增长。此外,当发现时延为1300个时隙时,LAND算法的邻居发现率接近于1,比Disco算法提高了近200个时隙。

图7 节点邻居发现率
4 结 语
针对MLDC-WSNs的发现邻居节点问题,提出时延感知的邻居发现LAND算法。LAND算法通过共享邻居节点信息,先构建初始邻居集,然后,再有选择地唤醒节点,并将邻居集划分为两个子集。再依据节点移动距离估计因节点移动而新构建的节点集。仿真结果表明,相比于Disco和GDB算法,LAND算法降低了发现邻居节点的时延,并提高邻居发现率。
