似然函数导数法在DOA估计中的研究

廖 晖，孟祥东，何 强

(南京电子技术研究所，江苏 南京 210039)

0 引 言

掌控空中情报资源是预警机的基本使命，拥有信息技术优势并夺取制信息权将成为战争胜负的关键[1]。由于雷达向空中辐射大功率电磁波且受到地杂波的限制，预警机在电子干扰、反辐射导弹、隐身飞机和低空突防等威胁面前面临严重的生存危机[2]。无源探测方式预警机雷达不发射电磁波，只接收目标辐射的电磁波来获取目标的信息，因而不易被地方侦察系统所发现，免受反辐射导弹的攻击，极大地提高了预警机的生存能力[3]，是预警机获取战场态势和情报资源的有效补充和重要手段[4]。DOA估计技术是无源探测最重要的技术之一，MUSIC

算法是应用最广泛的超分辨DOA估计方法，文章提出的单脉冲似然函数导数法计算量小，适合工程应用。

1 MUSIC算法

MUSIC算法的核心原理是以信号子空间与噪声子空间的正交性为基础，划分空间来进行参数估计[5-6]，工程应用算法流程如图1所示。

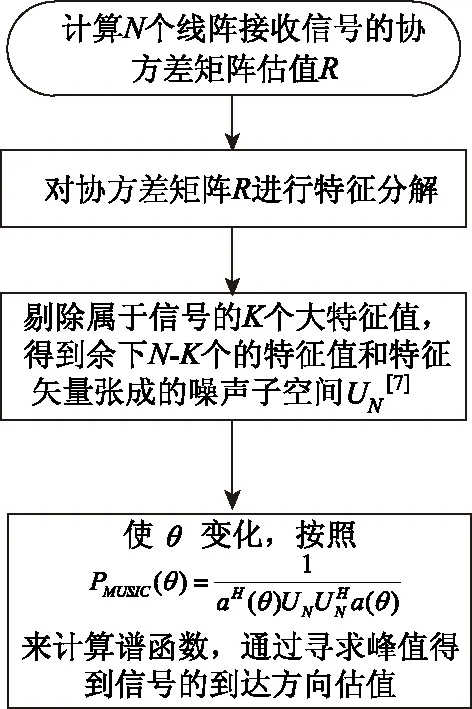
图1 MUSIC算法的流程

从MUSIC算法的流程可以看出，MUSIC算法在工程应用中面临两个问题，一是θ搜索的步进问题，过疏角度估计不准，过密增加计算时间；二是x(t)的协方差矩阵R的特征值分解计算量问题。

2 单脉冲似然函数导数法

2.1 似然函数导数法原理

假设雷达阵列为一个N元线阵，如图2所示，阵元间距d为雷达的半波长。

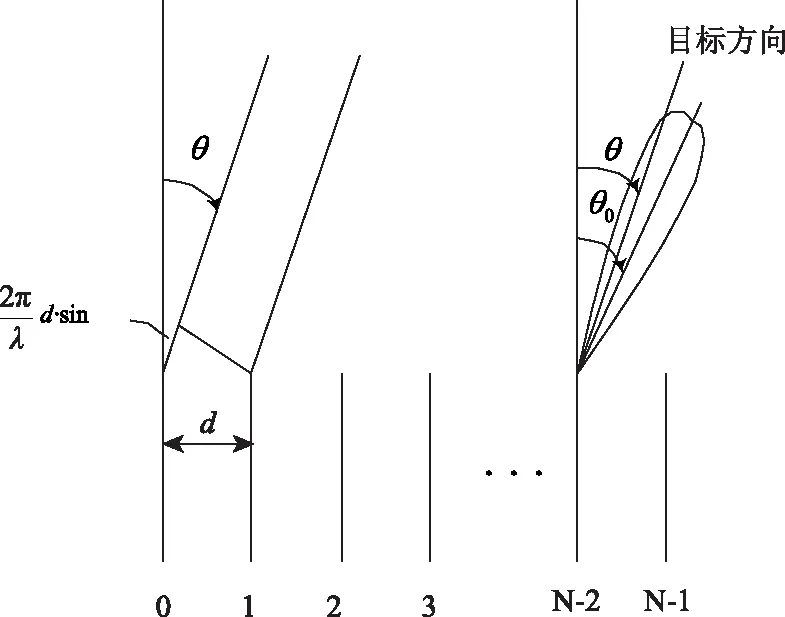
图2 N元雷达线阵

假设噪声服从独立零均值的平稳Gauss分布，一个N元线阵的一次数据快拍表示为：

z=a(θ)b(t)+n(t)

(1)

其中b(t)表示实际接收信号的复振幅;n(t)表示各个阵元所接收到的噪声组成的N元向量。此时数据z的极大似然函数为：

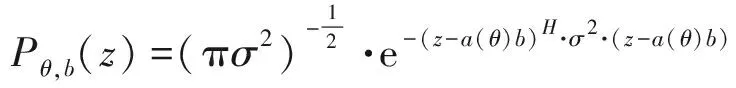
(2)

式中,σ2为的白噪声方差，根据极大似然原理，参数θ的最优估计应该使得上述联合概率密度函数的值取得最大。此时对应着-(z-a(θ)b)H·(z-a(θ)b)最小。根据最小二乘原理有b=[a(θ)H·a(θ)]-1·a(θ)H·z时对应着波束回波功率S(θ)=|a(θ)H·z|2最大，因此，为了估计θ，只需寻找使得功率函数达到最大的θ值即可。

构造函数设为：

F(θ)=ln (S(θ))=ln (|a(θ)H·z|2)

(3)

基于Taylor展开的一阶线性逼近：

F(θ)=F(θ0)+F′(θ0)(θ-θ0)+Ο(θ-θ0)2

(4)

对F′θ在目标实际所在位置θmax处进行一阶Taylor展开可得：

Ο(θ-θ0max)2

(5)

根据极值定理，当F′θ(θ)=0时，θmax是使得F(θ)为极大似然估计的自变量值，即：

(6)

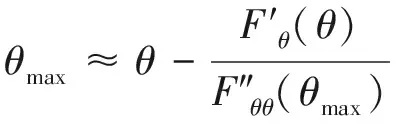
(7)

根据修正自适应单脉冲导数公式[8]，假设au(θ)=a′(θ)，a(θ0)≈a(θmax)，x=b(t)+n(t)：

(8)

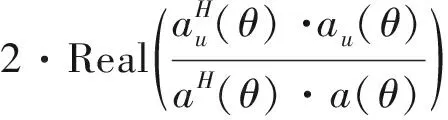
(9)

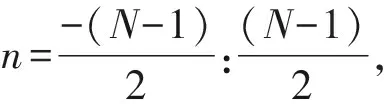
(10)

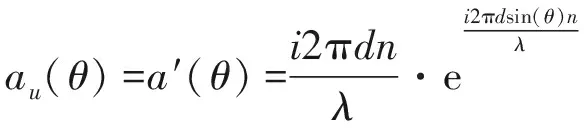
(11)

(12)

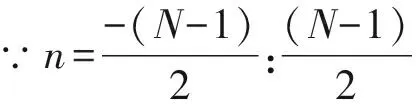
公式(10)、(11) 、(12)代入公式(7)，得到

(13)

(14)

把波束指向角θ0代入公式(14)，即可求得信号到达角度。

根据上述讨论，单脉冲似然函数导数法的流程如图3所示。

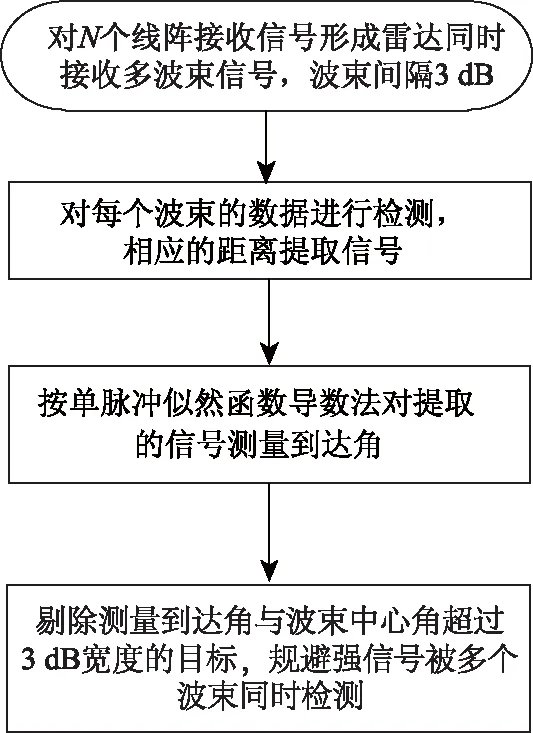
图3 单脉冲似然函数导数法的流程

从单脉冲似然函数导数法的流程可以看出，与MUSIC算法相比，θ搜索的步进是固定的，与雷达的波束排布一致，同时也避免了协方差矩阵R及其特征值分解。

2.2 似然函数导数法仿真分析

仿真参数设置如下：线阵，16个阵元，波束指向从-90°～90°，共步进32个波束，波束中心间隔6°，波长0.6 m，阵元间距0.3 m。分别从-45°、0°和 30°注入3个信号源，由于本文只考虑DOA估计的性能，假设3个信号源距雷达的距离一致，同时忽略检测部分，对每个波束信号源所在的距离数据直接测角，仿真结果见图4(a)。 图4(b)～图4(d)分别波束在指向-45°、0°和 30°附近测角的局部放大图，由于雷达存在波束跃度，实际指向角分别为-43.55°、-2.90°和31.94°，信号源分别与波束指向角相差了1.45°、2.90°和1.94°，仿真的结果测量值分别为-45.01°、0.05°和29.98°，测量的误差分别为0.01°、0.05°和0.02°。

3 单脉冲似然函数导数法迭代测角

3.1 迭代测向原理

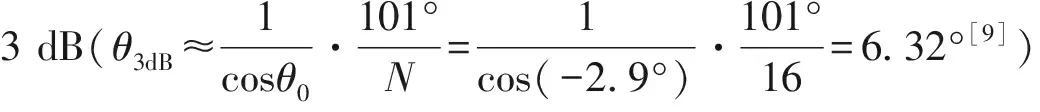
图4 似然函数导数法测角仿真分析

迭代后的角度估值如下：

θmax _iter=

(15)

根据上述讨论，单脉冲似然函数导数法迭代测角的流程如图5所示。

图5 单脉冲似然函数导数法迭代测角的流程

3.2 迭代测角仿真分析

仿真参数设置如3.2章所示不变，图6为迭代测角的结果，图6(b)～图6(d)分别波束在指向-45°、0°和 30°附近迭代测角的局部放大图，仿真的结果迭代之后信号测量值分别为-45.004°、-0.0097°和30.013°，测量的误差分别为0.004°、0.0097°和0.013°。

图6 单脉冲似然函数导数法迭代测角仿真分析

4 结 语

本文研究阵列天线测量信号来波方向的工程化快速算法，通过构造最大似然函数，并对最大似然函数求导数寻极值点的方法，得到精确的信号测量角度。理论分析和仿真结果表明，单脉冲似然函数导数法测角的精度与波束指向角的夹角相关，夹角越小，精度越高。另外还可以采用迭代测角的方法让波束指向角进一步与真值靠近来提高测角精度。单脉冲似然函数导数法迭代测角仅仅涉及矢量计算，计算复杂度为O(n2)，与MUSIC谱估计相比，避免了协方差矩阵特征分解(计算复杂度为O(n4))等复杂运算，易于工程实现。