基于同种映射的抗功耗攻击标量乘算法

李芳菊

(中原工学院信息商务学院，河南 郑州 450007)

0 引 言

椭圆曲线密码(Elliptic Curve Cryptography, ECC)是于1985年分别由Koblitz N和Miller V独立提出来的，与其它公钥密码算法相比，可以采用更短的密钥实现相同的安全级别，所以椭圆曲线密码既可以提高加解密速度且可以节省计算资源，非常适用于诸如智能卡、安全芯片等各类资源受限的密码设备中[1-2]。其中，标量乘算法是椭圆曲线密码最关键但也是最耗时的操作。但是功耗攻击针对标量乘算法具有较好的攻击效果，所以已成为当前标量乘算法的主要威胁之一。功耗攻击最早是由Paul Kocher于1998年最早提出的，主要通过测量密码装备运行时所泄露的功耗信息来实施攻击的，具有实现简单、成功率高等优势[3-4]。目前，标量乘算法抵御功耗攻击的主要措施大都是采用增加冗余操作的手段[5-7]。文献[8]提出一种基于带符号双基数系统的抗功耗攻击标量乘算法，该算法通过引入随机点对基点进行掩码来实现抗功耗攻击，然后采用带符号双基数系统对标量编码以优化运算效率。文献[9]提出一种基于带符号阶乘展开式抗功耗攻击标量乘算法，该算法通过引入随机点进行基点掩码及添加伪操作来实现抗功耗攻击，然后采用带符号阶乘展开式对标量编码以优化运算效率。文献[10]提出了一种基于带符号整数拆分形式的抗功耗攻击标量乘算法，该算法通过引入随机点进行基点掩码及标量分割来实现抗功耗攻击，然后采用带符号整数拆分形式对标量编码以优化运算效率。上述方案均是通过增加冗余操作来实现抗功耗攻击，虽然通过采用更高效的编码方式能够在一定程度上提升标量乘算法的效率，但与未施加抗功耗攻击措施的标量乘算法相比，仍然增加了计算开销。文中根据椭圆曲线同种映射理论，给出一种基于同种映射的抗功耗攻击标量乘算法(resisting power attack algorithm of scalar multiplication based on Homogeneous Mapping, HM)，通过变换椭圆曲线密码标量乘算法的形式来消除标量乘运算与泄露功耗信息的相关性，因此可以在不增加冗余操作的基础上实现抗功耗攻击。

1 椭圆曲线密码标量乘算法

定义1：假设存在域K，在其上定义一个椭圆曲线E：

E：y2+a1xy+a3y=x3+a2x2+a4x+a5

(1)

其中，ai∈K。式(1)也称为Weierstrass方程。

如果域K的特征不等于2或3，则通过变量的相容性变换，式(1)可变换为如下曲线方程：

E：y2=x3+ax+b

(2)

其中，a,b∈K。椭圆曲线E上点的集合及一个无穷远点O可以构成一个阿贝尔群。

在椭圆曲线E上定义两个不同的点P=(x1,y1)与Q=(x2,y2)，且P≠±Q。则这两个点相加可得P+Q=(x3,y3)的表达式如下所示：

(3)

椭圆曲线密码的标量乘法运算如下式(4)所示：

(4)

其中，k为标量，一般采用二进制编码表示，且编码长度为n比特，则可知标量k二进制编码表示形式如下式(5)所示：

(5)

标量乘算法采用二进制编码可以将标量乘运算分解为点加运算与倍点运算，如下式(6)所示：

Q=kP=(kn-12n-1+kn-22n-2+…+k12+k0)·P=

2{…2[2(2kn-1P+kn-2P)+kn-3P]+…+k1P}+k0P

(6)

则采用二进制编码的标量乘算法如下面算法1所示。

算法1 二进制编码的标量乘算法

输入：整数k，椭圆曲线上一点P；

输出：Q=kP。

(1) 令Q=O，其中O无穷远点；

(2) 对于变量i从n-1到0，则重复执行：

①Q=2Q；

② 如果ki=1，则有Q=Q+P；

(3) 返回Q。

由算法1可知，当ki=0时，执行倍点运算；当ki=1时，执行点加运算，由于倍点运算与点加运算的功耗不同，所以执行标量乘算法过程中会出现功耗差异，从而使得攻击者可以实施功耗攻击，根据功耗曲线与中间值的相关性获取密钥信息。

2 功耗攻击及其防御

简单功耗攻击通过测量密码算法的功耗信息差异来猜测所执行的操作及其次数，以此获取对应的密钥信息。抵御简单功耗攻击的主要方法是在ki=0时添加一次冗余点加操作，使标量乘算法在每一次循环运算均执行相同的操作，以此来消除功耗差异与密钥的相关性，实现抗功耗攻击的目的。

差分功耗攻击是采用功耗统计分析方法，首先根据测量的大量功耗曲线猜测密钥值，然后根据某个函数将这些曲线划分到两个集合中，并分别求平均来消除噪声，最后差分曲线，如果差分后的曲线有尖峰，说明猜测密钥正确，反之，则重新猜测密钥。其攻击过程主要为以下5个步骤[11]：

(1) 在密码算法执行过程中选择一个中间值；

(2) 测量每一个输入的明文对应的功耗曲线；

(3) 计算猜测的中间值；

(4) 采用某种功耗模型将猜测中间值映射成猜测的模拟功耗值；

(5) 计算猜测的模拟功耗值与实际测量功耗的统计相关性。

防御差分功耗攻击的方法主要有以下3种：

(1) 选择一个随机数与初始值进行异或，使得参与密码运算的是未知初始值，以掩盖原始初始值。

(2) 选择一个随机数与初始密钥进行异或，使得参与密码运算的是未知密钥，以掩盖初始密钥。

(3) 选择一个随机数与密码算法执行过程中的某个中间值进行异或，使得获取的中间值是未知的，以掩盖中间值与密钥的相关性。

3 椭圆曲线同种理论

定义2：如果存在椭圆曲线E1和E2，那么E1到E2的同种是一个同态，即φ:E1→E2满足φ(O)=O。

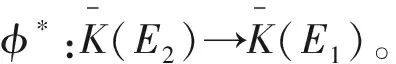
由于椭圆曲线是阿贝尔群，因此椭圆曲线间的映射构成了群。则从椭圆曲线E1椭圆曲线到E2的同种映射集合为：

H(E1,E2)={isogeniesE1→E2}

(7)

其中，isogeniesE1表示E1的同种椭圆曲线。两个同种椭圆曲线的求和为(φ+ψ)(P)=φ(P)+ψ(P)，所以φ+ψ为同态，也为同种。

4 基于同种映射的标量乘算法

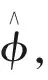
根据定义2，假设在K域上的两条椭圆曲线E与E′为一个非常值同态φ:E→E′，那么同种φ的次数可表示为：

(8)

假设φ为K域上椭圆曲线E和椭圆曲线E′之间次数为m的同种映射。其中，E：y2=x3+ax+b，E′：y2=x3+a′x+b′。令椭圆曲线点P为大素数，且有gcd(m,ordEP)=1(即m是ordEP可逆的)，定义r≡k/m(modordEP)。则可得椭圆曲线标量乘运算Q=[k]P的变换计算方式，如下式(9)所示。

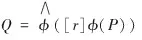
(9)

则可用如下同种映射模型来等价变换计算标量乘运算Q=[k]P，如图1所示。

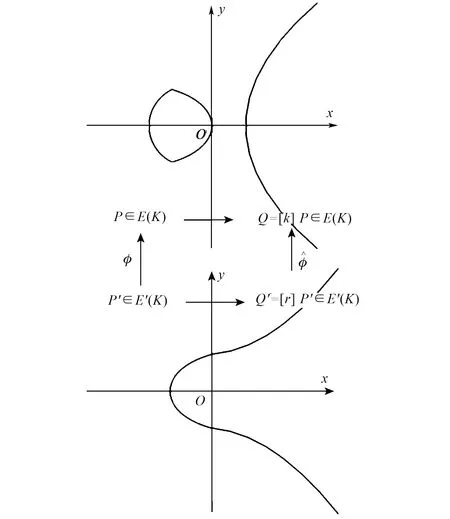
图1 椭圆曲线同种映射模型

由椭圆曲线同种映射模型可知，仅采用少量的域运算即可实现椭圆曲线上点的同种映射计算，通过随机选择一个随机同种映射来完成标量乘法运算，可以实现掩盖标量乘法运算的计算过程，攻击者无法获得与密钥信息相关的中间值，从而达到抵抗功耗攻击的目的。则下面给出基于同种映射的抗功耗攻击标量乘算法(HM算法)，如算法2所示。

算法2 基于同种映射的抗功耗攻击标量乘算法(HM算法)

输入：整数k，椭圆曲线E上一点P；

输出：Q=kP。

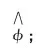
(2) 计算点P的同种映射P′=φ(P)；

(3) 按照公式r≡k/m(modordEP)计算出r的值；

(4) 在椭圆曲线E′：y2=x3+a′x+b′上，按照算法1的步骤计算同种映射后的标量乘运算Q′=rP′；

(6) 返回Q。

5 效率及安全性分析

6 结 语

现有的椭圆曲线密码抗功耗攻击方案为了能够同时兼顾安全和效率，一方面是通过增加冗余操作(如添加伪操作、引入随机数等)来实现椭圆曲线密码的抗功耗攻击，另一方面则利用新的标量编码方法(如带符号的双基数系统、带符号的阶乘展开式、带符号整数拆分形式)来降低标量乘法运算的计算开销。而所给基于同种映射的抗功耗攻击标量乘算法(HM算法)根据椭圆曲线同种理论，将原始标量乘法运算变换为同种椭圆曲线上的标量乘法运算，再根据对偶同种恢复原始标量乘法运算结果。所给M算法在执行过程中没有泄露与密钥相关的功耗信息，因此所给HM算法可以有效抵抗功耗攻击，并且没有增加冗余操作，另外也可以利用各类椭圆曲线密码标量乘快速算法来提升算法的整体运算效率。