一种优化无线传感网络的覆盖算法

许道强，吴 波，龚 贺，范照健，陈志国

(1.国家电网江苏省电力有限公司，江苏 南京 210000; 2.福建亿榕信息技术有限公司， 福建 福州 350003; 3.河北农业大学，河北 保定 071000)

0 引 言

无线传感网络(Wireless Sensor Networks, WSNs)内的节点具有感知、通信和计算能力，已广泛应用于灾害搜救、环境监测等其他工业应用。这些应用通过节点感测环境，并将感测数据传输至后台，进而监测环境的目的[2]。

在WSNs内运用最少的传感节点数覆盖最大的监测区域一直是WSNs的研究目标。文献[3]分析了三维随机覆盖连通问题，旨在以最少的节点数实现对监测区域100%的覆盖。而文献[4]研究了基于三维晶格模型的局部覆盖问题。

不同的应用对覆盖要求并不相同。有些应用要求对监测区域实现100%覆盖。而多数应用，并不需要对监测区域有100%的覆盖，只需要局部覆盖[4]，如图1所示。A区、B区、C区、D区对覆盖率的要求并不相同, 如D区对覆盖要求最高,达到90%。相比于D区, A区、B区、C区对覆盖要求较低, 分别为80%、60%和50%。

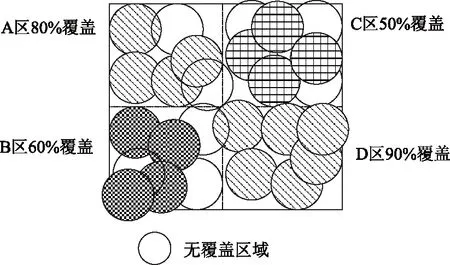
图1 局部覆盖等级

此外，WSNs一般由海量传感节点构成。这些节点可能存在一些特性差异。即使是同类型的传感节点, 也可能因故障原因呈现不同特性。因此, 多数WSNs表现出异构特性。为此, 本文以异构WSNs为研究对象, 分析异构WSNs的局部覆盖问题[5-7]。

文献[8]提出分布式的局部覆盖(Distributed Algorithm for Partial Coverage, DAPC)算法。在DAPC算法中，每个传感节点无需任何地理位置信息寻找冗余节点，并将这些冗余节点进入休眠状态。而文献[9]引用连通支配集(Connected Dominating Set, CDS)概念。利用构建CDS实现区域覆盖。文献[10]引用学习自动机分配活动节点和休眠节点，进而满足部分覆盖要求。然而，这些算法从局部覆盖角度讨论网络覆盖问题，同时，它们是以同构网络为研究对象。

为此，针对异构网络，提出概率模型的局部覆盖算法(Probability-based Partial Coverage, PPC)。PPC算法先计算传感节点的覆盖冗余度，再依据节点覆盖冗余度和对监测区域的覆盖面积，选择节点加入覆盖集。然后，覆盖集内的节点满足局部覆盖。仿真数据表明，提出的PPC算法能够以最少的节点数，满足覆盖要求。

1 约束条件及问题描述

将WSNs覆盖区域进行二维平面处理。令Ci和Ri分别表示第i个传感节点Si的通信半径、感测半径。一般感测半径大于通信半径。假定传感节点的通信区域和感测区域呈圆形[11]。

依据传感节点的通信半径和感测半径的不同, 将网络内N个节点划分t个类型。第i类传感节点表示为Si, 它的通信半径、感测半径分别表示为ri和Ri, 且1≤i≤t。

节点Si的感测区域表示为A(si,Ri)。A(si,Ri)表示以节点Si的位置si为圆心以Ri为半径的圆。节点Si不能感测A(si,Ri)区域的事件。类似地, 节点Si的通信区域也可表示为A(si,Ci)。

定义1: 在异构WSN内, 任意两个传感节点Si和Sj, 且1≤i,j≤t,∀{i≠j}, 则Ci≠Cj,Ri≠Rj。

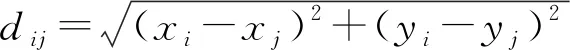
dij≤min(Ci,Cj)

(1)

其中(xi,yi)、(xj,yj)分别表示节点Si、Sj的二维坐标。

定义3: 如果节点感测区域内的局部区域的某点被不止一个节点覆盖, 则说该节点存在局部覆盖冗余。令ξi表示节点Si的覆盖冗余率, 其等于它邻居节点覆盖的区域面积与它自己覆盖区域面积之比。

2 PPC算法

为了选择合适的节点加入覆盖集, 利用概率模型估计节点Si的覆盖冗余度。并选择覆盖冗余度最低的节点加入覆盖集, 其他没选择的节点进行休眠, 进而以最少的节点实现目标的局部覆盖。

2.1 点的冗余覆盖

考虑节点Si的感测区域A(si,Ri), 如图2所示。令Y为一个随机变量, 其表示区域位置X离si的位置变量[12]。其中位置X离si的距离为x, 且0≤x≤Ri。因此, 变量Y概率密度函数可表示为:

fY(x)=2x/(Ri)2

(2)

图2 节点Si及Sj的感测和通信区域示意图

令pij(x)表示位置X被邻居节点Sj覆盖的概率。若X∈A(si,Ri)能被邻居节点Sj覆盖, 则节点Sj离位置X的距离大于Rj。

结合图1, 可推导pij值, 如式(3)所示:

(3)

依据式(3)可知,pij(x)值取决于位置X、si和min(Ci,Cj)。对于特定的一对邻居节点Si和Sj, 它们的有效通信区域A(si,min(Ci,Cj))是常数。

2.2 覆盖冗余度

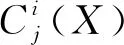
(4)

其中nij表示节点Si具有j类型的邻居节点数。

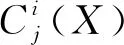
P(Di(X))=1-(1-pi1(x))ni1…(1-pit(x))nit=

(5)

利用积分, 计算P(Di(X))的期望值:

(6)

而节点Si的覆盖冗余度ξi的期望值E[ξi]可表示为:

(7)

将式(5)代入式(8)可得:

酒店使用社交媒体营销的目的。调查结果显示：社交媒体营销人员使用社交媒体营销时，最关注的是提高品牌知名度、提供产品信息和了解消费者需求。超过一半的酒店媒体高管认为社交媒体不应成为酒店创收的工具，而应成为酒店产品信息的宣传窗口。此外，有4家酒店提到招聘员工是他们使用社交媒体的另一目的。

(8)

2.3 覆盖集

提出PPC算法旨在: 以最少的节点数满足局部覆盖要求。为此,PPC算法从覆盖冗余度择优选择传感节点加入覆盖集。

首先, 随机选择一个传感节点加入覆盖集，然后再从该节点的邻居节点中选择覆盖冗余度最低的节点加入覆盖集[13], 重复执行, 直到满足局部覆盖要求。

先随机选择一个传感节点Sk加入覆盖集Φ。令Nk表示节点Sk的一跳邻居节点集; 再计算Nk内节点的覆盖冗余度，并选择覆盖冗余度低的节点加入Φ, 如式(9)所示:

Φ=Φ∪Si

(9)

其中|Nk|表示Nk内节点个数。

再检测Φ内节点的覆盖区域是否满足局部覆盖要求? 。如果满足要求, 就停止向覆盖集内添加节点。否则, 就从Φ内节点的邻居节点中选择覆盖冗余度和对监测区域覆盖面积大的节点加入覆盖集。从Φ内节点的邻居节点中选择节点加入覆盖集, 能够保持网络的连通性。

以图3为例阐述构建局部覆盖集的过程。图3(a)为网络的拓扑结构。假定选择节点5加入覆盖集。而节点2,4,8,9,6是节点5的邻居节点。而节点4覆盖区域的面积最大。因此, 选择节点4加入Φ。

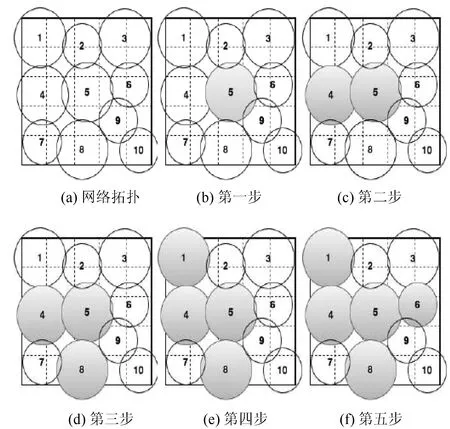
图3 PPC算法构建覆盖集示例

Φ={4,5}内节点的邻居节点为{1,2,8,9,6}。再从{1,2,8,9,6}中选择覆盖冗余度低和覆盖面积大的节点加入Φ。而节点8的覆盖面积大,且覆盖冗余度低。因此, 节点8加入覆盖集。如图3(c)所示。再将节点1加入覆盖集。最后, 将节点6加入覆盖集。选择节点6的原因在于:尽管节点2, 6, 9的覆盖面积相同, 但是节点2和节点9的覆盖冗余度高于节点6。

3 性能仿真

表1 两类传感器节点参数

3.1 实验一

本次实验分析不同类型的节点数对覆盖集内节点数的影响。为了简化描述，将覆盖集内的节点称为覆盖节点。在满足局部覆盖要求u条件下，覆盖节点数越少，性能越好。

图4显示了m1∶m2=0∶1和m1∶m2=1∶3两种情况下的覆盖节点数。从图4可知，覆盖要求u越高，所需的覆盖节点数越多。例如，在u=0.6时所需的覆盖节点数低于u=0.95。

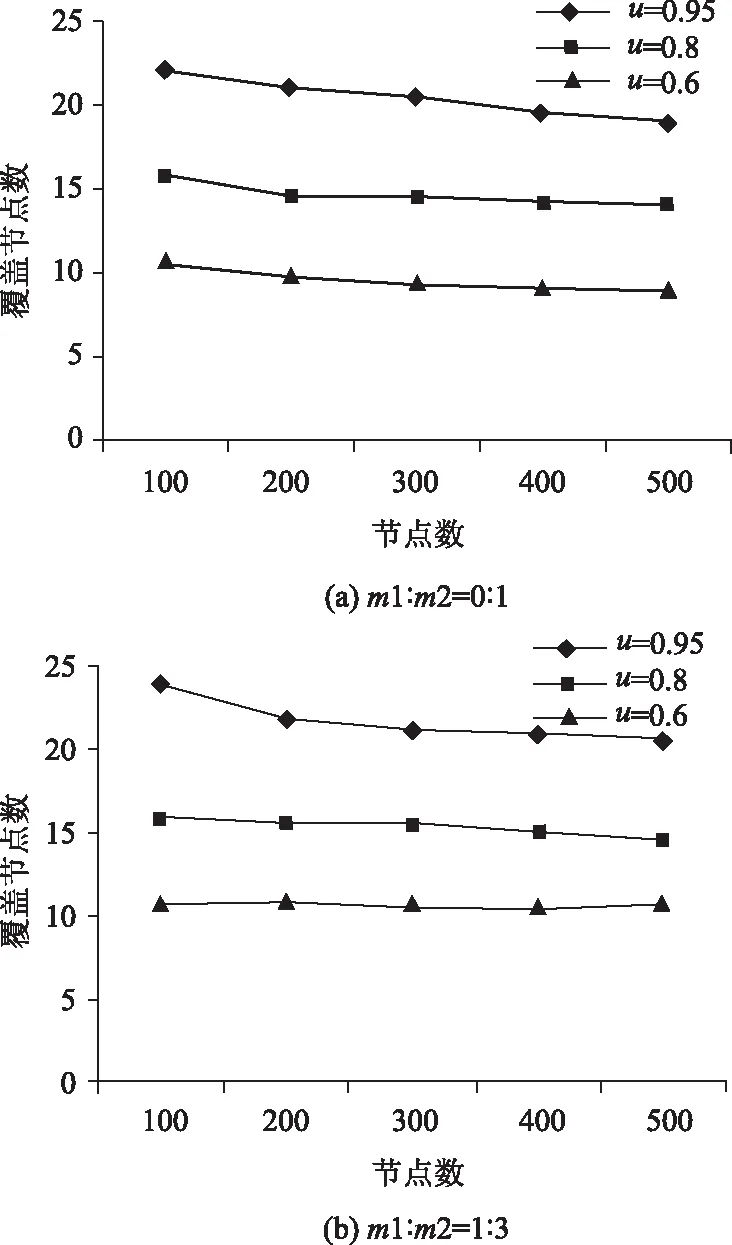
图4 活动节点数

此外，对比图4(a)和4(b)可知，在m1∶m2=1∶3网络环境下所需的覆盖节点数大于m1∶m2=0∶1网络环境下的覆盖节点数。原因在于：第二类传感节点的感测半径大于第一类传感节点的感测半径。相比于m1∶m2=0∶1,m1∶m2=1∶3网络环境下的第二类传感节点更少。因此，它需要更多的传感节点加入覆盖集，进而满足覆盖要求。

3.2 实验二

本次实验进行对比分析，选择DAPC、CDS和PCLA算法作为参照。实验参数：100个节点分布于100 m×100 m。并考虑m1∶m2=1∶0和m1∶m2=0∶1这两种情况。m1∶m2=1∶0意味着100个节点全是第一类节点；而m1∶m2=0∶1意味着100个节点全是第二类节点。由于这两类节点的通信半径和感测半径不同，通过对比分析这两种情况下的覆盖性能，可获取通信半径和感测半径对覆盖性能的影响。

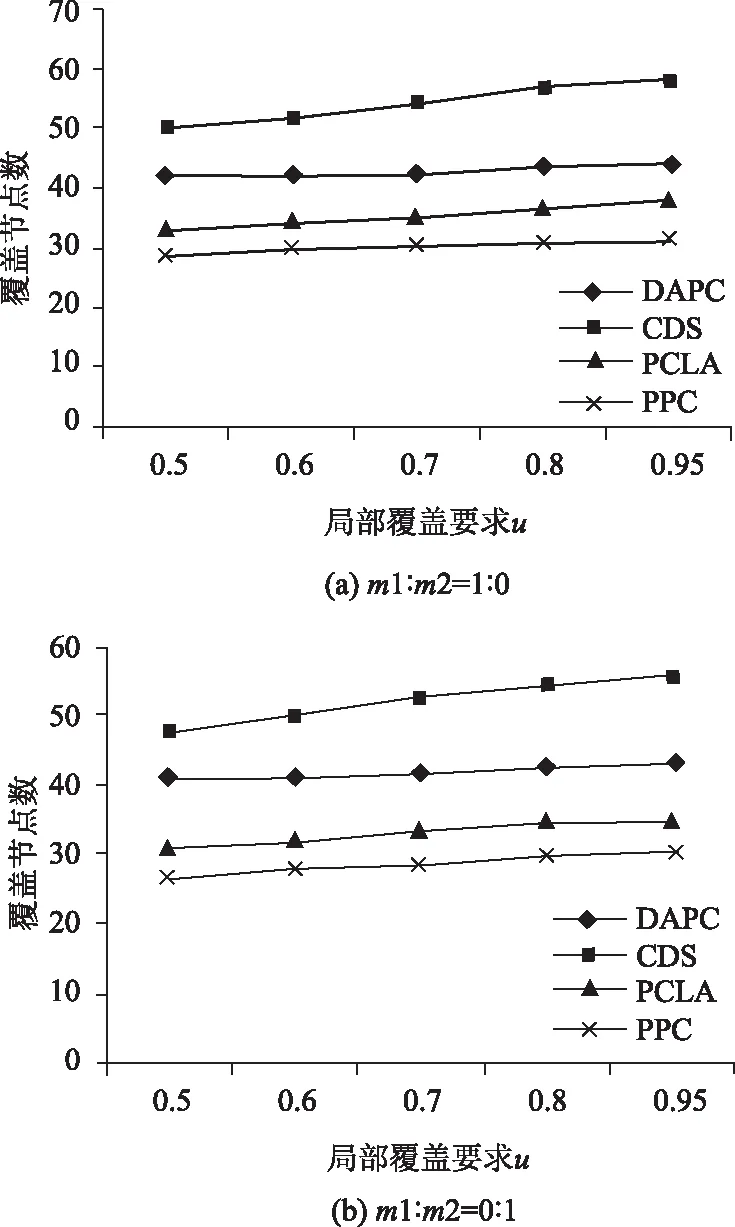
图5 活动节点数(实验二)

从图5可知，提出的PPC算法所需的覆盖节点数优于DAPC、CDS和PCLA算法。原因在于：PPC算法通过覆盖冗余度和对监测区域的覆盖面积选择节点加入覆盖集，进而能够以最少的节点数覆盖监测区域。

此外，对比图5(a)和5(b)不难发现，m1∶m2=0∶1情况下所需的覆盖节点数少于m1∶m2=1∶0情况。原因在于：第二类传感节点的感测半径大于第一类传感节点。

4 结 语

针对异构WSNs网络的局部覆盖问题，提出基于概率模型的局部覆盖算法PPC。PPC算法先利用概率模型估计传感节点覆盖冗余度，再通过覆盖冗余度择优选择节点，将这些节点加入覆盖集。并由覆盖集内节点覆盖监测区域。实现数据表明，提出的PPC算法降低了覆盖集内节点数。

本文只研究WSNs的局部覆盖问题，旨在以最少的传感节点覆盖监测区域。但是，并没有分析PPC算法的复杂度以及节点能耗问题。这将是后期的工作方向。