偏航对预测零转弯半径割草机连续翻滚特性的影响
2019-12-22王新彦袁春元佘银海
叶 烨,王新彦,袁春元,佘银海,张 权
(江苏科技大学 机械学院,江苏 镇江 212000)
0 引言
零转弯半径割草机(Zero Turning Radius Mower)可以实现原地转弯且工作效率高,因此常应用于斜坡、洼地等复杂工作环境。随着ZTR割草机的广泛应用,安全事故也不断出现,对于ZTR割草机驾驶安全性的要求也日益提高。
农用车辆安全性的研究主要集中在农用车辆初始失稳、失稳后非连续翻滚特性及失稳后连续翻滚特性上。1971年,Larson和Liljedahl[1]发展了一种数学模型,模拟了拖拉机侧翻并预测侧翻发生条件。2009年,Mashadi和Nasrolahi[2]发明了一种控制系统,通过建立拖拉机斜坡侧翻模型分析其横向稳定性,并改变拖拉机重心位置以防止翻滚。1974年,Davis和Rehkugler[3]发明了具有10自由度的三维拖拉机模型,通过主轴角速度来量化拖拉机翻滚运动。1979年,Chisholm[4-6]根据力和位移的平衡方程建立了一个数学模型,描述了拖拉机的斜坡稳定性。
在割草机连续翻滚特性的研究上的进展包括:1973年,Schwanghart[7]建立了农用拖拉机连续翻滚特性的动力学原始模型,该模型被作为带有翻滚保护装置的农用拖拉机的测试标准(OECD CODE6[8]);2002年,美国农业工程学会采纳已存在的OECD标准作为前驱割草机翻滚保护装置的设计标准(ASAES547[9])。真正涉及割草机连续翻滚特性研究的是Wang[10]和Ayers[11]在拖拉机连续翻滚预测模型基础上,将割草器尺寸及由割草器宽度引起的初始偏航加入了模型,并且分析了割草器尺寸对翻滚性能的影响。
该领域存在的问题:割草器宽度不仅引起初始偏航,而且产生动态偏航。实验研究表明:动态偏航对于准确预测在斜坡上作业的ZTR割草机的连续翻滚特性有着较大影响。
为了准确预测ZTR割草机在斜坡上的连续翻滚特性,依据国际最新标准ISO 21299-2009[12],首先建立了动态偏航和滑移动力学方程;然后将动态偏航和滑移加入了Wang的连续翻滚模型,并修正了该模型;最后,以ZTR割草机为对象实验验证修正后模型的正确性,并分析了偏航对连续翻滚特性的影响。
1 基于偏航的ZTR割草机连续翻滚特性预测模型
前期的研究发现,由于ZTR割草机的割草器安装在中间(见图1),其横向失稳后的运动特性发生了变化。动态偏航是影响割草机翻滚特性的重要因素之一,本预测模型的目的就是建立动态偏航与割草机的翻滚特性之间的定量关系,最终获得停止割草机连续翻滚的翻滚保护装置临界高度(Critical ROPS Height,简称CRH)。
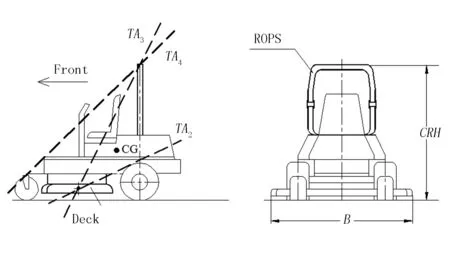
图1 割草器位置及其两个转动轴的定义
1.1 偏航的定义
割草机横向失稳到ROPS触地后,割草机发生滑移、翻滚、偏航和俯仰4种运动的合成运动,属于6自由度复杂运动。为分析偏航对割草机连续翻滚的影响,本文建立了一个ROPS触地后割草机偏航初始模型,如图2所示。其中,割草机偏航分为初始偏航和动态偏航。图1中,割草器触地后首先绕转动轴TA2(Tipping Axis 2)转动;随着翻滚的继续,ROPS(翻滚保护装置)碰撞到地面,地面下陷;随后,割草机绕着TA3(Tipping Axis 3)转动。
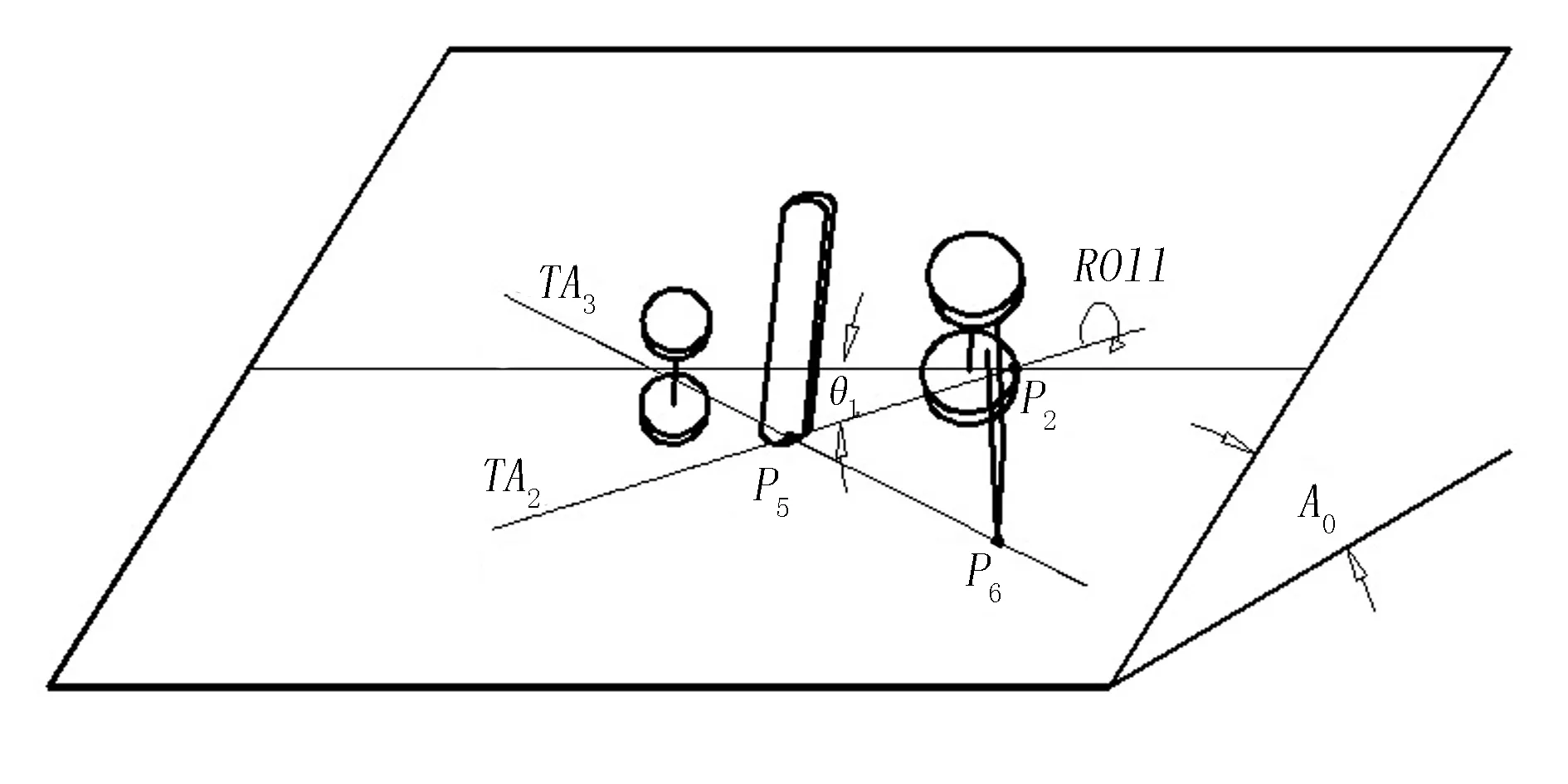
图2 偏航初始模型


图3 ZTR割草机动态偏航和滑移运动分解示意图
为了建立ZTR割草机斜坡偏航初始模型,做以下假设:
1)忽略两次翻滚之间瞬时的俯仰和翻滚运动;
2)忽略割草机各非线性因素,将割草机看作一个整体;
3)忽略油箱油位对动态偏航和滑移过程中对割草机重心位置和运动的影响;
假定偏航过程中轮胎与草地的摩擦力系数μ4、割草器和ROPS与草地的摩擦力系数μ56为常数。
1.2 割草机动态偏航和滑移力学模型
为分析ZTR割草机动态偏航和滑移特性,对ZTR割草机偏航初始模型进行简化受力分析,可得ZTR割草机动态偏航和滑移力学模型,如图4所示。

图4 ZTR割草机动态偏航和滑移力学模型
根据所建立的力学模型可知:ZTR割草机Z方向受力平衡,绕X轴力矩平衡,绕Y轴力矩平衡。平衡方程为
GK=N2+N5+N6
(1)
(2)
(3)
GK=mg×cosA0
(4)
GIJ=mg×sinA0
(5)
GI=GIJ×cosθ1
(6)
GJ=GIJ×sinθ1
(7)
式中A0—初始位置斜坡坡度角;
θ1—翻滚轴线TA2与水平线夹角(即初始偏航角位置)。
P2、P5和P6点处正压力方程为
(8)
1.3 第一步分运动(割草机滑移)
正如前面所假设的,为了研究问题,将割草机的失稳后的运动分为两步,即沿斜坡滑移和纯动态偏航。下面首先研究第1步分运动,即沿斜坡的滑移(无偏航)。
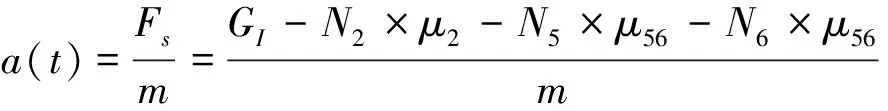
(9)
式中Fs—割草机滑移合力;
a—割草机滑移加速度。
将式(8)代入式(9),即可得割草机滑移加速度a(t)方程。
同时,可得滑移距离Ls(t)方程为

(10)
(11)
滑移距离是后续割草机翻滚特性的研究重要参数,如求割草机滑移过程中损失的能量计算、割草机动能和势能的变化计算等。
1.4 第二部分运动(割草机动态偏航)
由于ZTR割草机在侧翻碰撞时存在冲量,使ZTR割草机质心速度发生变化,导致ZTR割草机将发生动态偏航。结合图4,可得ZTR割草机动态偏航时的动力学方程为
GI×t=m×(V2-V1)
(12)
系统因冲量而增加的动能为
(13)
(14)
式中V1—侧翻碰撞时质心速度的分量,垂直于J轴,平行于斜面;
θ2—动态偏航角。
2 连续翻滚模型修正
2.1 动态偏航和滑移能量损失修正
割草机失稳后拥有的动能越少,其连续翻滚的趋势越小,驾驶员的伤亡率也越低,因此准确预测割草机动态偏航和滑移时的能量损失尤为重要。
ZTR割草机动态偏航和滑移时的能量损失,主要是摩擦力做功损失的能量。根据ZTR割草机动态偏航和滑移运动分解,将能量损失分解为滑移时摩擦力做功损失能量Es及偏航时摩擦力做功损失能量Ey。滑移时摩擦力做功为
(18)
偏航时摩擦力做功为
(19)
E损=Es+Ey
(20)
2.2 质心速度修正
ZTR割草机动态偏航和滑移发生在割草机绕TA2翻滚至P6触地发生沉陷后(此时割草机重心线速度为V1)与割草机准备绕TA3翻滚之前(此时割草机重心线速度为V3),如图5所示。所以,根据能量守恒定律可得
(21)
因此,可以得到割草机准备绕TA3翻滚之前割草机重心绕TA2质心速度V3为
(22)

图5 割草机从P6触地发生沉陷到准备绕TA3翻滚之前
2.3 割草机连续翻滚预测模型的判定
获得割草机质心速度V3后,根据能量守恒方程可以计算出割草机绕TA3轴转动到重心(CG)处在接触点C3的正上方时的质心速度VZ(见图6)。根据此时的质心速度VZ就可以判断割草机的翻滚特性,即连续翻滚、非连续翻滚和临界状态。临界状态定义为:翻滚过程中割草机的动能刚好可以使其重心(CG)处在接触点O的正上方,此时重心(CG)的线速度VZ=0。非连续翻滚定义为:翻滚过程中割草机的动能不足以使重心(CG)超越接触点O的正上方,重心(CG)只能处在过接触点O的垂线的右侧,割草机最终又返回到斜面上;连续翻滚定义为:翻滚过程中割草机的动能足以使重心(CG)超越接触点O的正上方,重心(CG)到达过接触点O的垂线的左侧(斜坡下坡的方向),此时重心(CG)的线速度VZ>0。根据上述翻滚过程的分析,建立了零转弯半径割草机连续翻滚预测模型,并编写了MatLab程序。因此,对于一定的割幅,改变ROPS的高度,就可以使得VZ=0,即势能和所需动能相等。对应的ROPS高度即为割草机不发生连续翻滚时的翻滚保护装置(ROPS)的最小高度(CRH)。

图6 割草机绕TA3轴翻滚
2.4 编写MatLab程序
根据上述理论分析编写MatLab 程序,流程图如图7所示。该程序的输入参数为ZTR割草机尺寸参数、质量、质心位置参数、转动惯量及摩擦因数等,程序的输出为翻滚特性(连续翻滚、非连续翻滚和临界状态)及CRH。
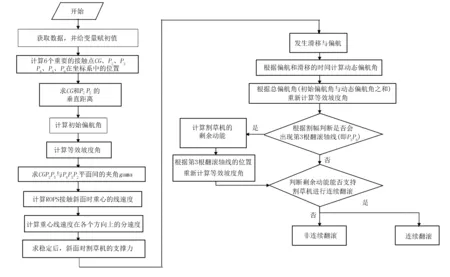
图7 主程序流程图
3 试验与讨论
3.1 试验设备及方案
为验证加入动态偏航和滑移模型的准确性,以维邦WBZ12219K-S型ZTR割草机为对象,进行了实地翻滚试验。割草机整机质量(MC)为468.5kg,其他参数及各个参数所代表的意义如表1及图8所示。

表1 维邦WBZ12219K-S的参数 m
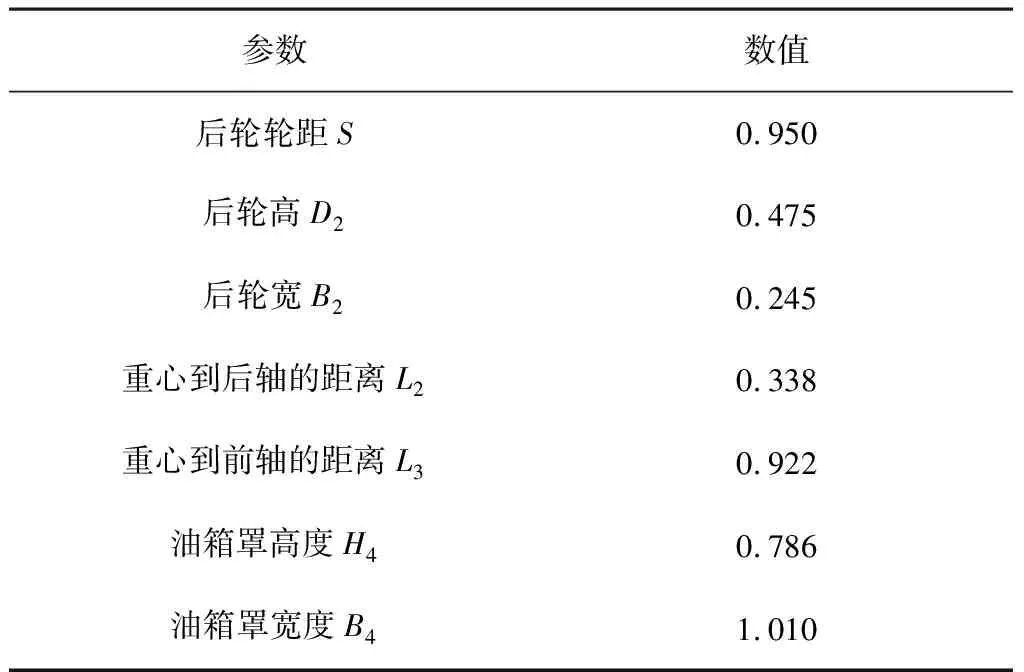
续表1

续表1

图8 维邦WBZ12219K-S型ZTR割草机参数
表2为试验过程的实际参数。

表2 试验参数
试验方案如图9~图11所示。

图9 裸机(ROPS 1.65m,30°)

图10 1.2m割幅(ROPS 1.65m,20°)

图11 2.3m割幅(ROPS 2.036m,21.4°)
首先将割草机停在初始台上,然后升高初始台直至与翻滚台齐平,最后用初始台将割草机掀翻。分别测试裸机、割草器宽度为1.2m和1.8m的割草机翻滚特性。由于割草器宽度为2.3m的割草机外形尺寸较大,故翻滚试验在扬州某高尔夫训练场进行。
3.2 模型预测结果与试验结果比较
定性的研究可以从表3看出:在割草器宽度较小时,试验及理论模型结果存在误差;在宽度较大时,试验及理论模型结果一致。为了定量研究理论模型预测结果与试验结果的误差,引入相对误差的概念(公式23)。计算出如下3种情况的试验结果与理论模型结果的相对误差值(见表4和图12)。由表4可知,最大相对误差为17.6%。
(23)
3.3 误差分析
相对误差主要来自于:①实验平台的不平度; ②实验过程中割草机上各种液体的流动而导致的前后质量分布变化;③建立模型过程中忽略的因素,如俯仰运动等。
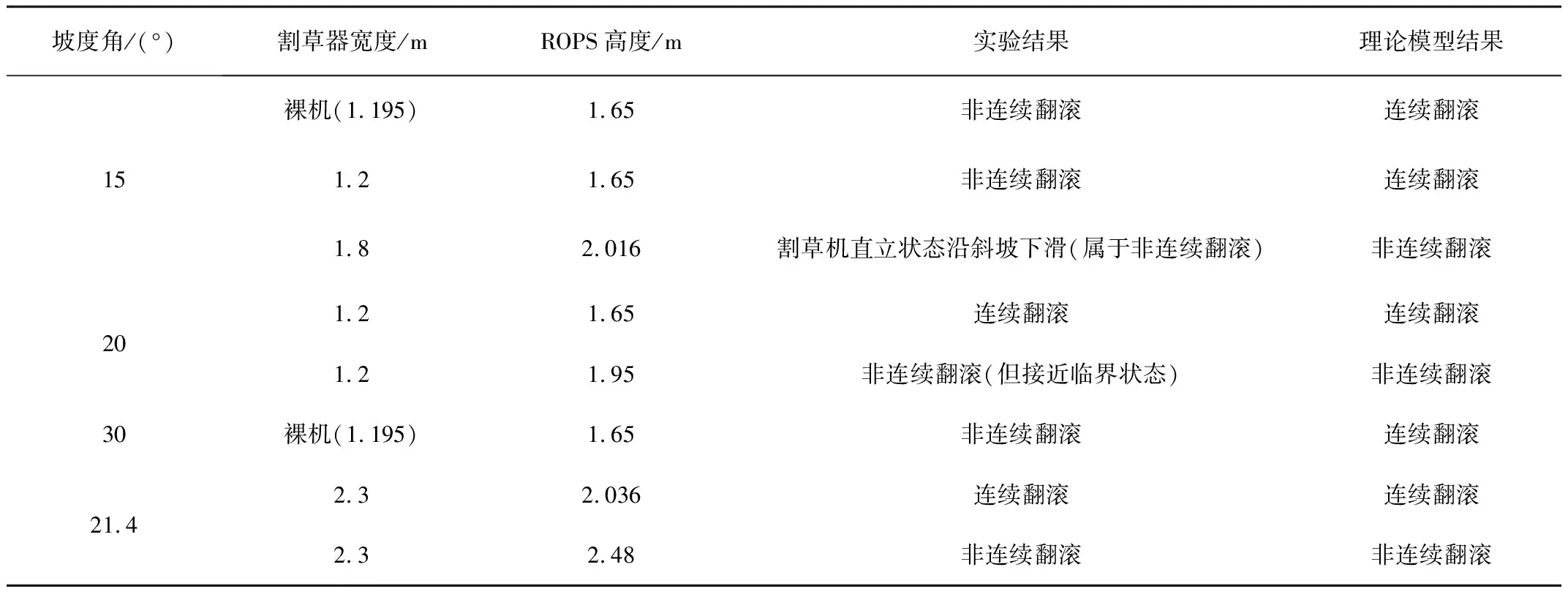
表3 试验及理论模型结果对比
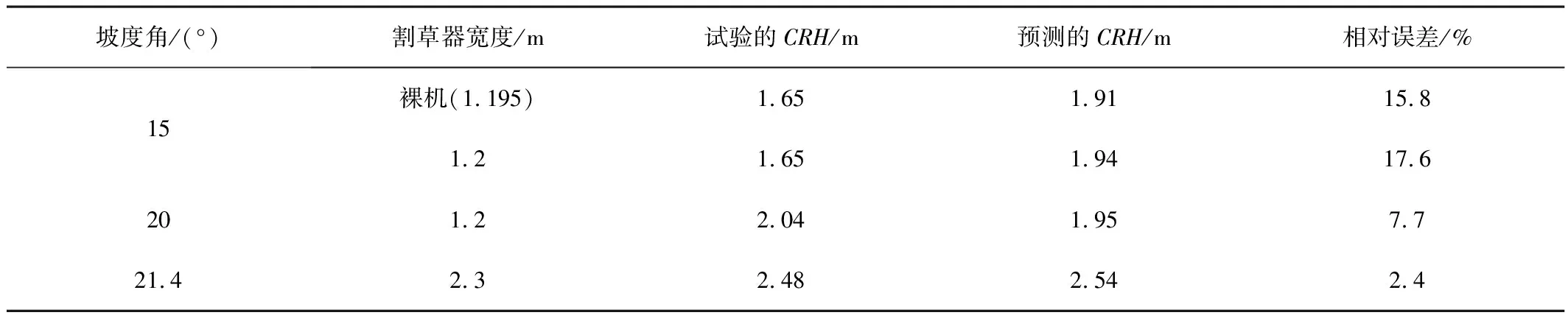
表4 试验及理论模型结果相对误差值

图12 预测的CRH值与实验的相对误差对比
3.4 偏航与CRH的关系讨论
初始偏航和CRH的关系如图13所示。

图13 初始偏航与CRH的关系
从趋势来看,初始偏航较小时,CRH对初始偏航角变化表现的很敏感;随着初始偏航角慢慢增大,它对CRH的影响慢慢变小并趋于平缓。图13中存在两个明显的拐点:第1个拐点出现在极限点3(割草器宽度增加到1.4m左右时),原本存在的翻转轴线TA4(P6与P8的连线)将不复存在,这会使得割草机的翻滚难度突然增加;第2个拐点出现在点6,原因是初始偏航角增大且草地与割草器的接触点不断后移,增加了割草机翻滚中的势能,使得翻滚变得较为容易。图14为动态偏航角与CRH预测值的关系。通过选取割草器宽度及改变ROPS高度直到临界状态发生(即CRH),此时输出的中间变量为动态偏航角。动态偏航角为过程中的变量,它与斜坡摩擦因数、翻滚初始割草机的势能及割草机在翻滚中的重力分配等有关系,故动态偏航角与CRH呈非线性关系。
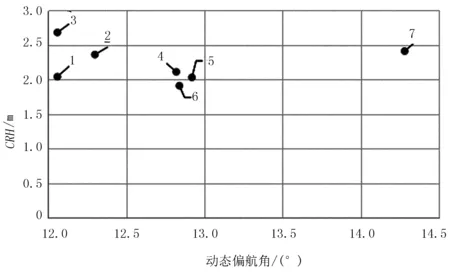
图14 动态偏航与CRH的关系
4 结论
本文在建立模型时加入了偏航运动,使CRH的预测结果能更加接近真实试验结果。试验表明:在角度较大的情况下,模型能较准确地预测出ZTR割草机的CRH。
试验中,B5及μ56是影响连续割草机翻滚特性的主要因素。因此,在满足割草机设计标准的情况下,应尽量增加割草机割幅,并可以通过改变割草器表面材料形状和粗糙度来提高割草器与坡面摩擦因数,以降低割草机的翻滚趋势。
该预测模型可以帮助ZTR割草机选取合适的翻滚安全保护装置的高度。合适的高度既可以保证操作人员的生命安全,又可以尽可能地提高割草机的通过性,从而间接地提高了割草机的工作效率。
