二级垛式悬臂式挡土墙的受力与变形特征分析
2019-12-21
(1.国网安徽省电力有限公司建设分公司, 合肥 230061; 2.安徽送变电工程有限公司, 合肥 230022)
1 研究背景
悬臂式挡土墙由钢筋混凝土制作的立臂式面板、墙趾板、墙踵板3部分组成,主要靠底板上的填土重量来维持稳定的挡土结构,宜在石料缺乏、地基承载力较低的地段采用。通常,悬臂式挡土墙的高度不宜>6 m[1]。
既有文献主要关注一级悬臂式挡土墙[2-5],而事实上,在某些情况下可采用二级甚至多级垛式悬臂式挡土墙,该类型挡土墙也逐渐引起工程与学术界的关注。梁波等[6]通过数值分析方法模拟施工工况,考察了二级垛式悬臂式支挡结构的墙背变形和填土受力特点;王景环等[7]基于土的塑性极限分析理论,考虑滑裂面上填土黏聚力及填土与二级新型悬臂式挡土墙墙背接触面上的黏着力,研究了挡土墙土压力受力分析模式,给出了土压力强度、土压力合力、土压力作用点的理论计算公式;张勇等[8]对多阶悬臂式挡土墙支护结构在填土区工程应用中发生的失稳破坏案例进行分析,通过有限元方法计算出填土在不同内摩擦角、黏聚力取值下挡土墙的应力-应变关系的变化趋势,揭示了边坡形成整体滑移破裂面而导致悬臂式挡土墙失稳的机理;梁桥等[9]的理论解析及实例分析结果表明二级悬臂式挡墙基底应力分布比单级悬臂式挡墙要合理,也更偏向于安全。
然而,关于二级垛式悬臂式挡土墙的设计与计算方法还不成熟,其受力与变形性质还有待进一步探讨。为此,本文基于有限元方法,对二级垛式悬臂式挡土墙的土压力及填土变形进行对比分析,通过变换土体强度参数探讨垛式挡土墙稳定性变化规律,为准确把握二级垛式悬臂式挡土墙的荷载特征提供参考。
2 有限元计算模型
针对某一典型二级垛式悬臂式挡土墙进行分析,上下两级挡土墙尺寸相同,挡土墙高度H=5 m、墙踵板长度L=3.4 m,钢筋混凝土板厚50 cm,填土表面超过上墙顶部的高度h=1.0 m,且上墙顶部的填土设置坡率1∶2的倾斜面,挡土墙的计算构型如图1所示。

图1 悬臂式挡土墙计算构型
鉴于挡土墙纵向长度较大且横截面大小和形状沿轴线长度不变,采用平面应变有限元进行分析。原地基与填土材料采用Mohr-Coulomb理想弹塑性模型,挡土墙为钢筋混凝土结构,其强度较高,可按线弹性材料考虑。各土层及挡土墙的计算参数见表1。
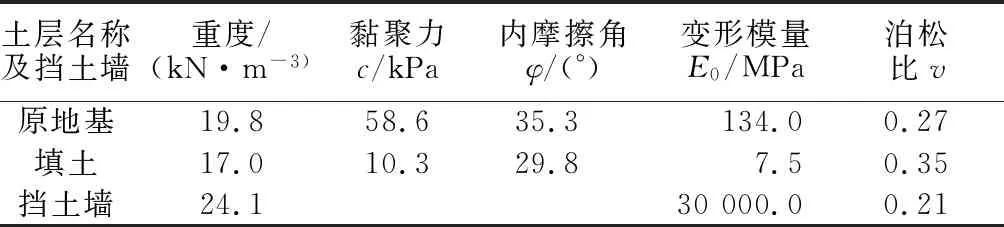
表1 各土层及挡土墙的物理力学参数
为了模拟挡土墙与土体之间的界面特性,可在两者之间设置无厚度的接触面单元。采用摩擦系数R来反映挡土墙与土体之间的相互作用程度,根据相关文献的实验数据[3],并结合墙后土体的物理力学参数,本次计算中取R=0.65。
数值计算的边界条件为:底部采用固定边界条件(不发生水平位移和竖向位移),两侧为水平方向位移约束条件。采用15节点的三角形单元对计算模型进行网格剖分,并在挡土墙与填土接触的部位及土层分界面加密网格剖分,图2给出了有限元网格的划分情况。
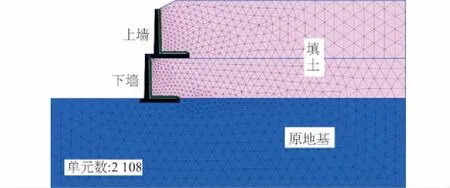
图2 有限元网格划分
原地基土的沉降在挡土墙施工前早已完成,可通过逐步激活挡土墙与填土单元来模拟各施工工序,并采用强度折减有限元法[10-13]来考察挡土墙的滑裂面位置及安全系数。
3 计算结果分析
基于有限元方法,对不同参数情况下的挡土墙土压力与填土变形进行了考察,得到了二级垛式悬臂式挡土墙的基本特征。
3.1 填土变形特征
施工结束后,墙后填土内部的侧向位移等值线分布如图3所示,上墙墙背与下墙墙背竖向断面处的侧向位移如图4所示,填土内部的竖向沉降如图5所示。图3与图4中的负值表示侧向位移与x轴方向相反。
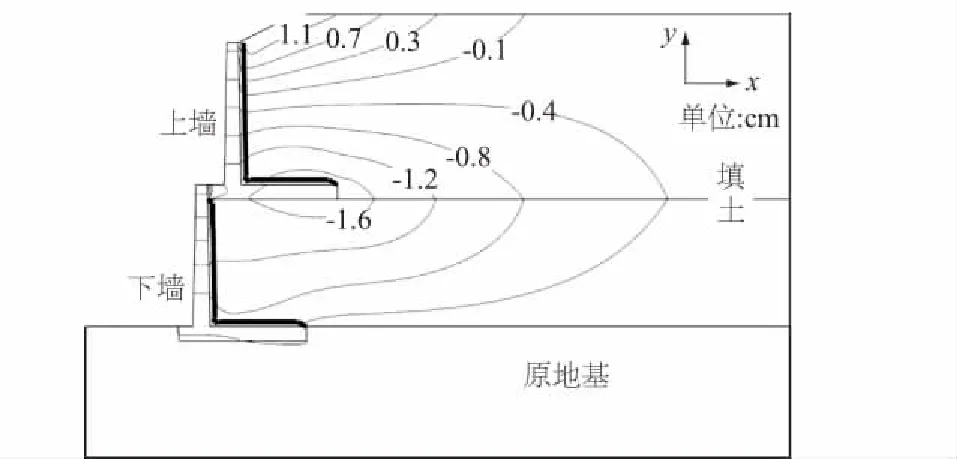
图3 填土内部侧向位移等值线分布
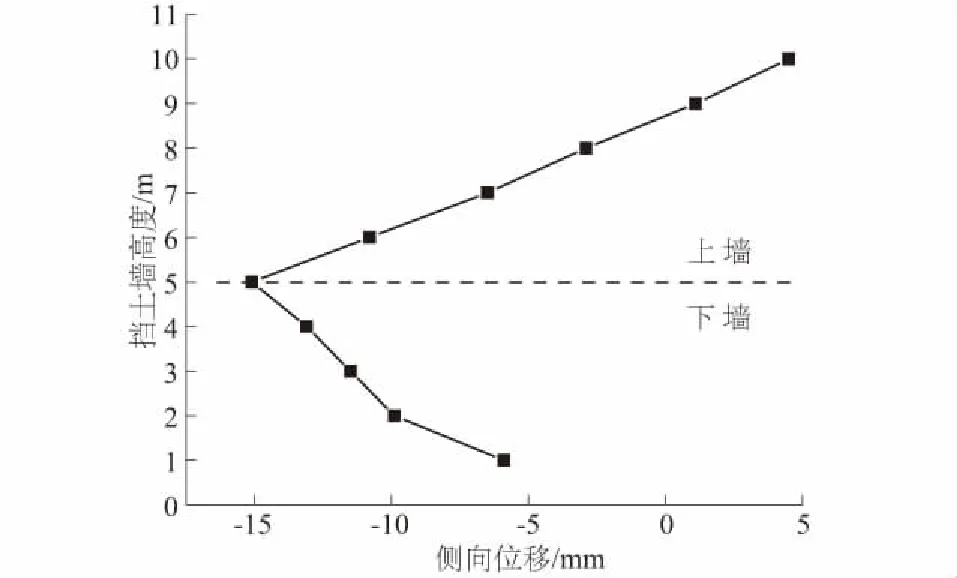
图4 挡土墙墙背侧向位移分布
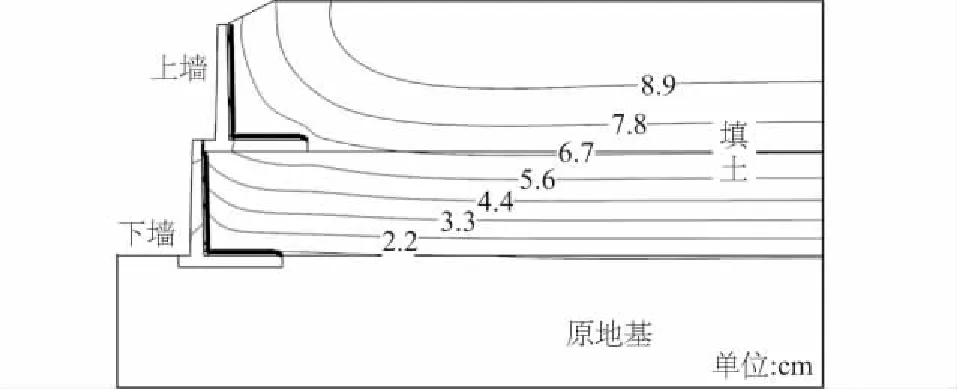
图5 填土内部竖向沉降等值线分布
由图3与图4可知,填土的侧向位移最大值发生在上墙的墙踵板附近,其值为1.6 cm,方向指向临空面。以上墙墙踵板的根部为中心,距离墙根越远,填土的侧向位移越小。特别地,距上墙顶部1.15 m位置处的填土侧向位移为0,距上墙顶部附近<1.15 m范围内填土的侧向位移为正值,即方向指向临空面的反方向;距上墙顶部>1.15 m范围内填土的侧向位移为负值,方向指向临空面。可见,下墙范围内填土的侧向位移均向临空面方向发展,而上墙的下部范围内填土的侧向位移向临空面方向发展,上墙顶部附近填土的侧向位移向临空面相反方向发展。这种二级垛式悬臂式挡土墙填土的侧向位移变化规律,与传统的单个悬臂式挡土墙填土侧向位移显然不同。通常,单个悬臂式挡土墙的填土侧向位移均指向临空面。
这种填土的侧向位移变化规律与挡土墙结构的特征有关。二级垛式悬臂式挡土墙的上墙与下墙本质上是相互分离、互不相关的,下墙的特征与传统单个悬臂式挡土墙的特征相似,下墙具有向临空面倾覆的趋势。
但对于上墙而言,一方面其墙踵板压在下墙填土面的顶部,下墙范围内填土发生的位移使其墙踵板难以保持水平状态,上墙随着填土位移而发生变位运动;另一方面,上墙部分范围内的填土又压在上墙的墙踵板上,进一步加剧了上墙的变位运动。结合填土沉降规律可知,上墙将产生一定的背离临空面的旋转,最终造成上墙顶部一定范围内填土的侧向位移向临空面相反方向发展。
图6进一步表达了上墙与下墙的运动趋势示意图。由图6可见,由于上墙与下墙之间无强有力的连接关系,上墙与下墙体现出不同的运动趋势,这种趋势是由土体的变形与挡土墙的受力共同决定的。
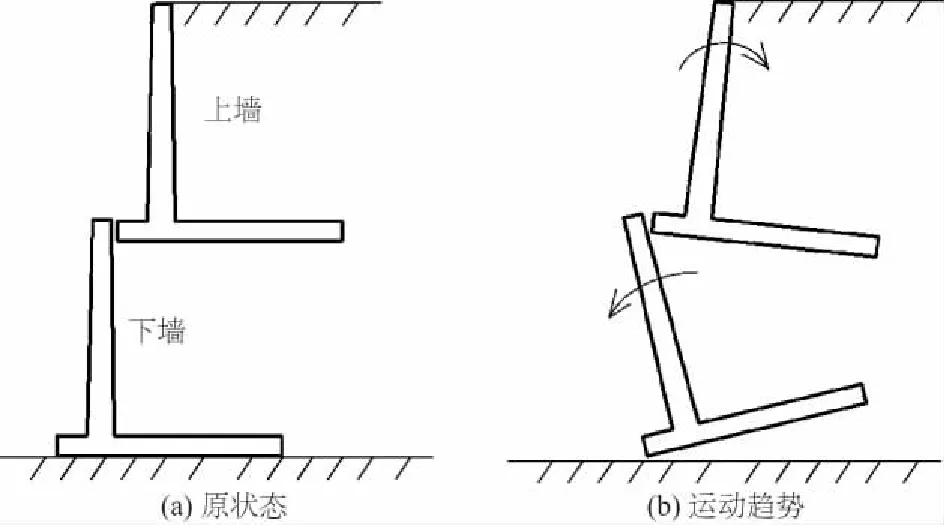
图6 二级悬臂式挡土墙运动趋势示意图
下墙的墙踵板压在沉降已完成的原地基土层上,其稳定性相对较高。而对于上墙,其墙踵板压在新填筑的土体上,若填土的压实度不够,导致上墙与填土一起发生较大的移动。可见,上墙的运动不仅与其本身受到的荷载大小有关,还与其下方填土的密实度有关。为了提高二级垛式悬臂式挡土墙的整体稳定性,填土(特别是上墙底部的填土)的密实度应满足要求,优先选用压缩性小、强度高的砂砾石填筑在上墙墙踵板的底部。
3.2 挡土墙的土压力特征
二级垛式悬臂式挡土墙墙踵板受到的竖向土压力分布及其特征如图7所示。由图7可见,上墙与下墙墙踵板受到的竖向土压力均呈现非线性特征,距离墙根越近,竖向土压力越小;距离墙根越远,竖向土压力越大。
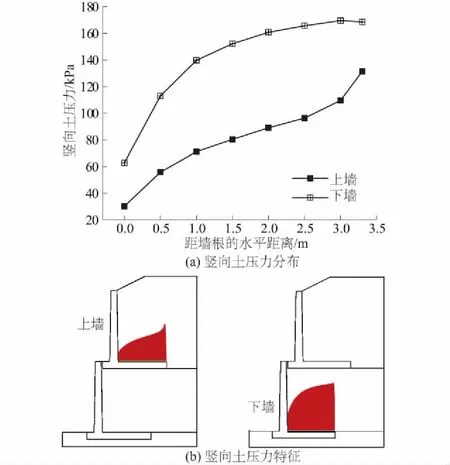
图7 二级垛式悬臂式挡土墙墙踵板竖向土压力分布及其特征
对于上墙而言,其墙踵板受到的位于墙根处的竖向土压力最小值为30.2 kPa,墙踵板端部的竖向土压力最大值为132.8 kPa。若将填土顶部1.0 m厚的倾斜填土简单等效为0.5 m厚的水平填土,该墙踵板位置处填土的自重应力为(5+0.5)×17.0=93.5 kPa,可见部分位置上的墙踵板竖向土压力远小于上覆土重,而另外部分位置上墙踵板的竖向土压力大于上覆土重,土压力系数最大值为1.42。
对于下墙而言,其墙踵板受到的位于墙根处的竖向土压力最小值为62.8 kPa,墙踵板端部的竖向土压力最大值为174.8 kPa。若将填土顶部1.0 m厚的倾斜填土简单等效为0.5 m厚的水平填土,且忽略上墙自重的影响,下墙墙踵板位置处填土的自重应力为(10+0.5)×17.0=178.5 kPa。下墙墙踵板竖向土压力的最大值与该位置处的上覆土重基本相当,但部分位置上的墙踵板竖向土压力远小于上覆土重。由于填土的变形与挡土墙的变位,导致填土内部产生应力拱,使上墙与下墙墙踵板受到的竖向土压力与上覆土重存在明显的差别。
二级垛式悬臂式挡土墙墙背受到的侧向土压力分布及其特征如图8所示。由图8可见,上墙与下墙墙背受到的侧向土压力均呈现非线性特征。上墙墙背的侧向土压力分布与传统的单个悬臂式挡土墙类似,侧向土压力的非线性特征已有实验数据证实[14-15]。
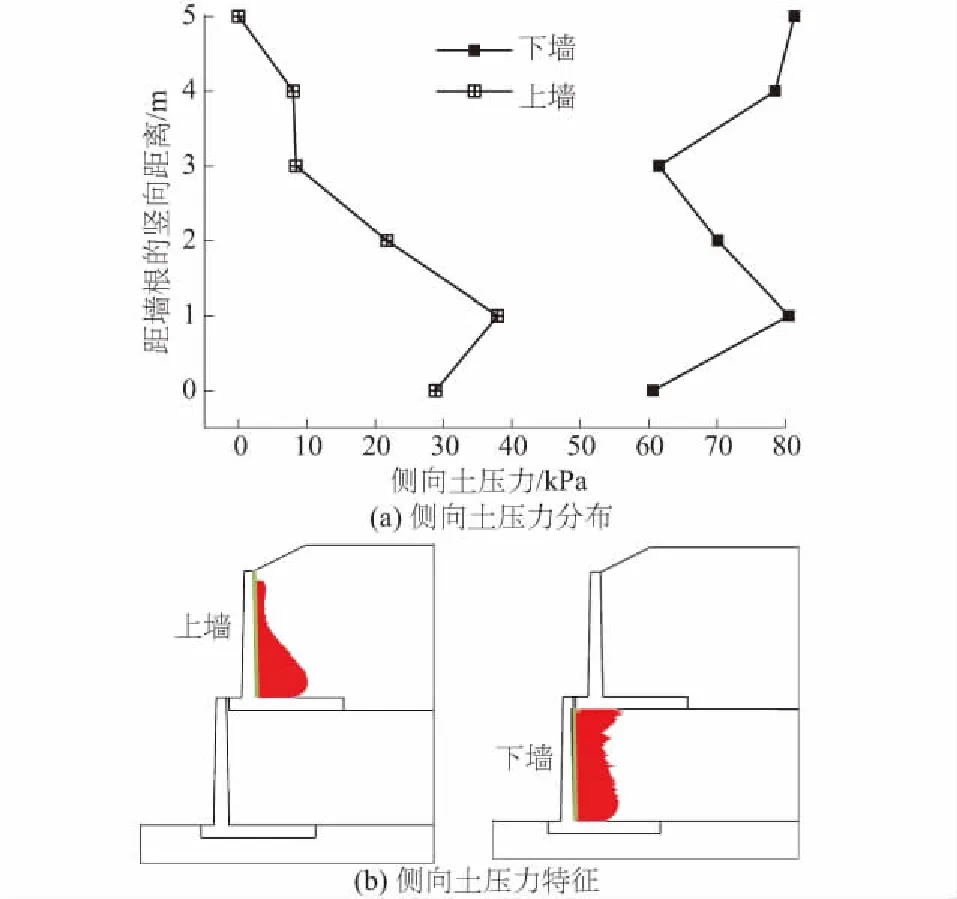
图8 二级垛式悬臂式挡土墙墙背侧向土压力分布及其特征
对于下墙而言,上墙的刚性墙踵板压在下墙填土的顶部,导致下墙顶部的侧向土压力较大,是应力集中的体现。下墙侧向土压力最大值为81.3 kPa,位于上墙墙踵板底部处。在上墙墙踵板压力、填土不均匀沉降、下墙自身的变位等共同影响下,下墙墙背的侧向土压力呈现非线性。二级垛式悬臂式挡土墙的下墙墙背侧向土压力值难以通过现有的计算理论得到。目前既有文献中对下墙侧向土压力的研究较少,还有待通过试验测试进一步深入探讨。
3.3 挡土墙的抗滑稳定性
基于强度折减有限元法来计算二级剁式挡土墙的抗滑稳定性,其操作步骤为[3]:在有限元计算中,先对于某一假定的强度折减系数Ftrial,将各土层的原始强度参数黏聚力c与内摩擦角φ按式(1)同时折减。
cr=c/Ftrial,φr=arctan(tanφ/Ftrial) 。
(1)
式中cr,φr分别为折减后的黏聚力与内摩擦角。
以此对边坡进行弹塑性有限元计算,如果根据一定的失稳判据[10-13]确定边坡达到极限平衡状态,则与此相对应的强度折减系数Ftrial就是挡土墙安全系数Fs,否则对于新假定的折减系数重复计算,直至土体达到临界极限平衡状态。
基于强度折减有限元法,计算得到了二级垛式悬臂式挡土墙失稳时滑裂面的位置,如图9所示。可见,填土中有2个滑裂面,第一滑裂面基于下墙墙踵板根部贯穿于填土中,第二滑裂面基于上墙墙踵板根部贯穿于上部填土中。
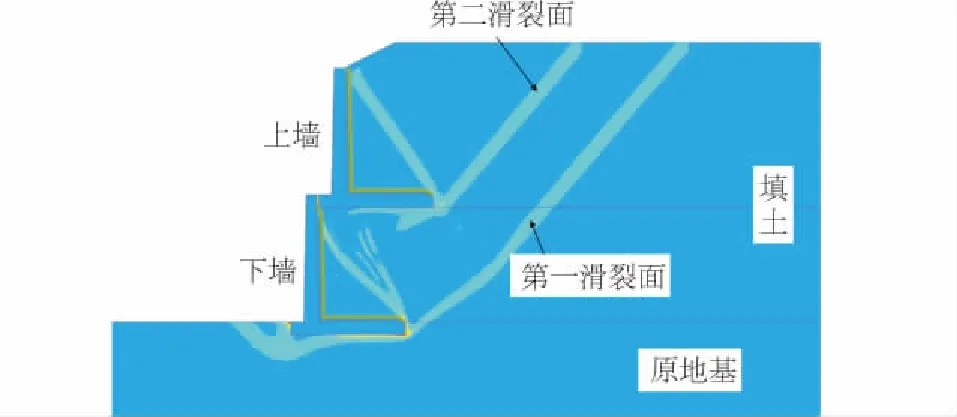
图9 二级垛式悬臂式挡土墙的滑裂面位置
工程中把出现第二滑裂面的挡土墙定义为坦墙[3,16]。但传统的坦墙通常是指同一挡土墙后方填土中出现的2个潜在的滑裂面,而本文的挡土墙实际上为上、下2个相互独立的悬臂式挡土墙,2个滑裂面分别对应上、下挡土墙,因此,本文中的2个滑裂面与传统的坦墙中滑裂面是有区别的。
当上墙与下墙的变位运动结束后,上墙的底部与下墙的顶部在水平方向上有交叠而未脱离时,上墙无法逃离下墙的约束而滑向临空面,此时整体的滑裂面往往是由下部的第一滑裂面控制。但当下墙无法约束上墙的运动时,填土的滑裂面可能是下部的第一滑裂面,也可能是上部的第二滑裂面,特殊情况下也有可能2个滑裂面同步发生。因此,为了维护整体的稳定性,上墙底部与下墙顶部在竖向的交叠高度越大越好。
挡土墙濒临失稳时填土内部的位移增量分布如图10所示。由图10可见,在第一滑裂面位置以上的填土内发生了较大的位移,且在上墙底部与下墙顶部交界处的位移增量较大,这与前述的侧向位移最大值位于该处取得了一致。对于二级垛式悬臂式挡土墙而言,除下墙底部承受较大的应力外,上墙底部与下墙顶部交界处也是薄弱环节,认识到这一点对准确把握垛式挡土墙的基本特征很有帮助。

图10 挡土墙失稳时填土的位移增量分布
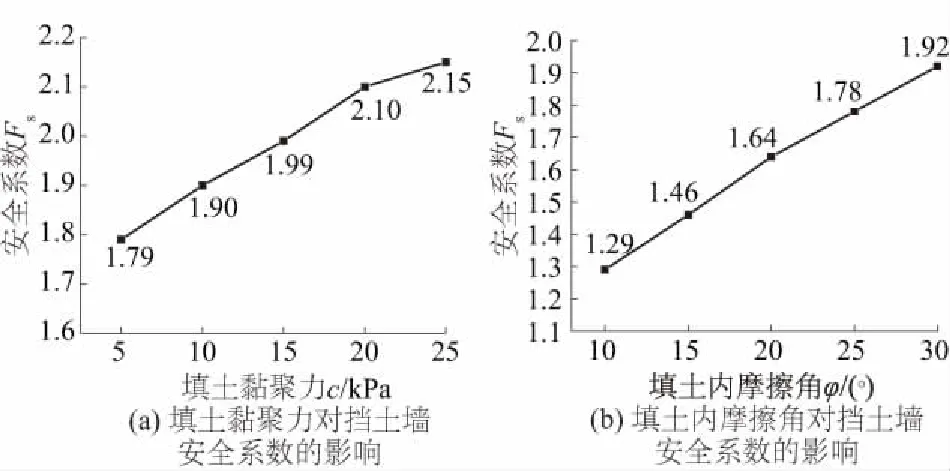
图11 填土黏聚力和内摩擦角对挡土墙安全系数的影响
计算得到挡土墙的安全系数Fs=1.91,填土的黏聚力与内摩擦角对挡土墙安全系数的影响如图11所示。本文所提二级剁式挡土墙属于“上墙无法逃离下墙的约束而滑向临空面”情况,故Fs=1.91是第一滑裂面控制下的稳定系数。由图11可见,挡土墙的安全系数随着填土的黏聚力或内摩擦角的增大而增大,工程实际中应选用强度较高的土体作为墙后填土,并确保压实度满足要求。
4 结 论
(1) 二级垛式悬臂式挡土墙填土的侧向位移最大值发生在上墙的墙踵板附近,方向指向临空面,以上墙墙踵板的根部为中心,距离墙根越远,填土的侧向位移越小。下墙范围内填土的侧向位移均向临空面方向发展,上墙的下部范围内填土的侧向位移向临空面方向发展,上墙顶部附近填土的侧向位移向临空面相反方向发展。
(2) 由于上墙与下墙之间无强有力的连接关系,上墙与下墙体现出不同的运动趋势,下墙具有向临空面倾覆的趋势,上墙随着填土位移而产生一定的背离临空面的旋转。
(3) 上墙与下墙墙踵板受到的竖向土压力均呈现非线性特征,距离墙根越近竖向土压力越小,距离墙根越远,竖向土压力越大。上墙墙踵板的最大竖向土压力大于上覆土重,下墙墙踵板竖向土压力的最大值与该位置处的上覆土重基本相当。
(4) 上墙与下墙墙背受到的侧向土压力均呈现非线性特征,上墙墙背的侧向土压力分布与传统的单个悬臂式挡土墙类似,上墙的刚性墙踵板压在下墙填土的顶部,导致下墙顶部的侧向土压力较大。
(5) 二级垛式悬臂式挡土墙失稳时填土中有2个滑裂面,第一滑裂面基于下墙墙踵板根部贯穿于填土中,第二滑裂面基于上墙墙踵板根部贯穿于上部填土中。
