基于混沌理论的明渠湍流速度特征

2019-12-21

长江科学院院报 2019年12期

(三峡大学水利与环境学院，湖北宜昌 443002)

1 研究背景

湍流流动在生活中很常见，它在时空内呈现出剧烈的脉动特性，属于连续的不稳定流动，是一个典型的非线性复杂动力系统。国内外众多学者对于湍流流动规律和生成机理的研究已取得了丰硕的成果，但对于湍流流动物理本质的研究仍有待深入。

在国外，Poincare于1903年提出了庞加莱猜想，并指出三体问题在一定范围内的解是随机的，这是一种混沌现象[1]。Lorenz[2](1963)在DeterministicNonperiodicFlow(《确定性的非周期流》)一文中，揭示了混沌现象具有不可预测性和初始条件极端敏感依赖性2个基本特点。Hénon和Heiles[3](1964)在研究混沌系统相空间临近轨道发散时，首次引入Lyapunov指数的计算，之后Lyapunov指数被正式应用在动力系统和各态遍历理论的研究中。Ruelle和Takens[4](1971)独立发现了动力系统存在复杂的吸引子。李天岩和Yorke[5](1975)在PeriodThreeImpliesChaos(《周期三蕴含混沌》)一文中，提出了混沌的数学定义，给出了一个混沌的判定定理。Takens[6](1981)提出了嵌入原理，为混沌时间序列分析奠定了理论基础。Borodulin和Kachanov[7](1989)在Couette-Taylor湍流流动试验的基础上，研究了奇怪吸引子问题，发现了流动系统存在着低维混沌。Hultgren[8](1992)通过管道间歇性湍流试验，证明了湍流流动与初始随机扰动的性质有关。在国内，汤一波等[9](1998)通过关联维度法分析了湍流脉动压力的混沌特征。李睿劬等[10](2002)对Kleba-noff平板边界层转捩流动进行了研究，建立了平板边界层湍流转捩与混沌之间的联系。沈学会等[11](2005)综述了混沌理论在湍流应用中的国内外研究进展。傅强等[12](2011)通过对Rayleigh-Benard对流温度信号分析，研究了混沌特征随空间变化规律。姚天亮等[13](2012)采用圆喷嘴空气射流试验，证实了射流一定距离内存在着混沌行为。张建伟等[14](2015)在双喷嘴水平对置撞击流混合器试验中，分析了其瞬时速度场的混沌特性。

综上所述，混沌理论在湍流研究中得到了广泛的应用，取得了大量的成果。但是，湍流是一种高度复杂的流动状态，在时间上，脉动尺度呈现出非周期性的涨落，在空间上，包含着多层次的结构，并具有一定的自相似性，是一种典型的随机和有序、混乱和结构统一的有机整体[15-16]。而大多数湍流研究探究了时间序列的混沌变化，没有考虑到时间序列的空间混沌变化特征，此外，对于天然明渠的湍流混沌特性研究较少。为此，考虑到湍流时空间的混沌特征变化，采用明渠水槽试验，在设计的工况下，采用ADV(Acoustic Doppler Velocimetry，声学多普勒测速仪)测量湍流速度场，通过计算明渠湍流空间不同位置湍流速度场的延迟时间、关联维度、Lyapunov指数和Kolmogrov熵等混沌特征参数，探究明渠湍流速度的空间混沌特征规律。

2 试验设计与混沌参数计算

2.1 试验装置

试验在矩形玻璃水槽中完成。矩形玻璃水槽主要由变频供水系统、输水管道、进水口、变坡玻璃水槽、出水口、蓄水库、多孔筛板构成。其中，变坡玻璃水槽两侧和底面都为有机玻璃，全长15 m，宽0.3 m，高0.3 m。明渠水槽装置见图1。

图1 明渠水槽装置

2.2 试验方案设计与数据采集

明渠水槽试验中，采用明渠均匀流流态，流量为0.021 m3/s，蓄水高度为0.18 m，平均流速为0.4 m/s，平均雷诺数为35 820。试验方案设计见图2，选择中上部分水流稳定的明渠玻璃水槽底部安装一块湍流控制板，湍流控制板宽0.3 m，长0.5 m，厚0.025 m，其上表面均匀粗糙，使其下游的一定空间范围内沿程和水深向上方向会产生一个持续衰减的湍流场，直到恢复明渠均匀流流态。沿湍流控制板下游中垂面依次选取6条测线，分别标记为B—G号，B号测线紧靠湍流控制板末端，相邻测线距离均为半个湍流控制板长度0.25 m。对于每条测线，沿渠底向上依次选取6个测点，分别标记为B1—B6、C1—C6、D1—D6、E1—E6、F1—F6和G1—G6,每条测线的第1个测点距离玻璃壁底0.02 m，相邻测点间的垂向间距均为0.02 m。随后，取出湍流控制板，在原B号测线位置上，沿渠底向上依次选取6个测点，各个测点与原B号测线上6个测点位置一致，记该测线为A号测线。

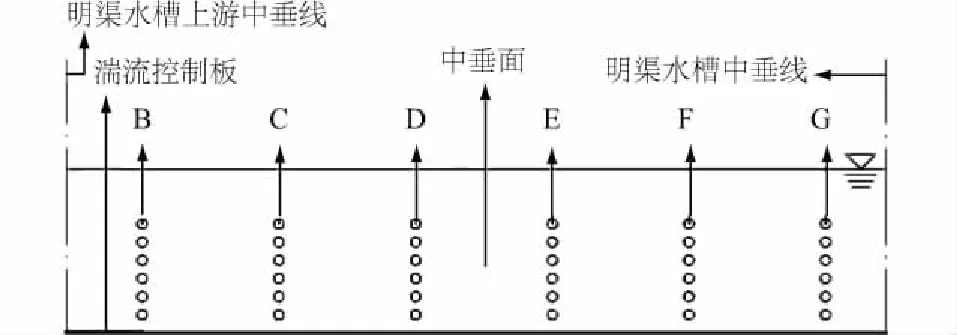
图2 中垂面试验方案设计

本试验湍流速度场采用ADV流速仪进行测量。本次试验设置ADV参数具体如下：采样频率为50 Hz，采样点的体积约为9×10-9m3，采样点位于探头下方0.05 m处，测量的误差为流速的1%范围以内，数据的采集与处理由配套软件Horizon ADV完成。

2.3 混沌特征参数计算

分析时间序列的混沌特性，首先需要进行混沌特性识别，其主要方法是通过计算时间序列的延迟时间、关联维数、Lyapunov指数和Kolmogrov熵等混沌特征参数来判别。其中，延迟时间表征动力系统时间过程行为反应敏感程度的大小，延迟时间越大，系统的行为反应敏感程度越小，系统运动的前后相关性越大；关联维数作为一种分形维数对系统的时间过程行为反应敏感，能够表征奇怪吸引子维数及其几何结构复杂程度，其值越大，动力系统中的奇怪吸引子几何结构越复杂；最大Lyapunov指数是刻画混沌轨迹的局域不稳定性和初始条件敏感依赖性的定量判据，是判断动力系统时间序列是否存在混沌和混沌特性强弱的一个重要依据，其值<0，说明时间序列不存在混沌特性，其值为0，说明时间序列处于临界状态，其值>0，且越大，混沌特性越强，反之其值越小，混沌特性越弱；Kolmogrov熵则是关于混沌系统的初始信息损失速率的度量，是对动力系统复杂的度量描述，是一个描述时间混沌特征的重要参数，Kolmogrov熵=0，表示该系统是有序系统，即该系统能够完全准确预测，Kolmogrov熵→，表示该系统是随机系统，能够进行统计平均预测，若Kolmogrov熵为>0的有限值，则该系统是混沌系统，Kolmogrov熵越大，系统对于初值越敏感[17]。

2.3.1 相空间重构

相空间重构是将一维的时间序列点x1,x2,…,xn(n为时间序列点的个数)映射到m维空间当中，使空间中原动力系统特征得到保持[18-19]，上述过程为

i=1,2，…，N。

(1)

式中：τ为延迟时间；N为重构后的相空间矢量的个数，N=n-(m-1)τ；X为相空间重构矩阵；Xi为相空间重构第i行数列；xi为第i个时间序列点。

2.3.2 关联维度的计算

关联维数的计算采用G-P算法[20]，在相空间重构的基础上，取相空间中点集{Xi}(i=1,2，…，N)的一点Xi={xi,xi+τ,…,xi+(m-1)τ}作参考点，计算另外N-1个点到它的距离，则可统计出落于以点Xi为中心、以小标量r为半径的体积元中的点的个数。对所有点重复这一过程，从而得到关联积分Cm(r)为

(2)

式中H(·)为Heaviside阶跃函数，即

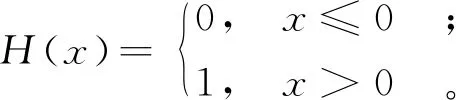
(3)

考虑n维相空间内的一个奇怪吸引子，设点集{yi}(i=1,2，…，N)是在奇怪吸引子上的一个很长时间序列的点集。现在用M(r)个大小为rn的n维小单元体覆盖住这个点集{yi}(i=1,2，…，N)的所有点，于是关联维度D2定义为

(4)

因此，画出双对数曲线lnCm(r)-lnr，取其中线性相关度比较好的部分，对其进行最小二乘线性拟合，拟合直线的斜率即为对应时间序列的关联维数D2。计算关联维数时，嵌入维数m和延迟时间τ的选取至关重要，分别采用常用的饱和维数法和自相关函数法确定[21-23]。

2.3.3 Lyapumov指数的计算

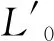
(5)

式中Lj=‖Xtj-Xtj(j)‖。

2.3.4 Kolmogrov熵的计算

目前，通常利用二阶关联熵K[25]来估算Kolmogrov熵，计算方法为

(6)

在计算中通常将K随m+1变化的稳定值作为Kolmogrov熵的估计值。

3 湍流速度的混沌特征分析

通过对明渠湍流控制板下游监测点的湍流速度信号的时间序列进行混沌特性分析，在已重构相空间的基础上，分别计算其延迟时间、关联维数、最大Lyapunov指数和Kolmogrov熵等混沌特征参数。对于明渠湍流而言，影响湍流速度混沌特征参数的因素众多。明渠湍流控制板、垂直方向上重力和水的脉动压力的合力、流向方向上上游来水的流向推力和下游水流的阻力对不同空间位置的湍流速度混沌特征参数影响程度均有差异，在这些因素的共同作用下，探讨湍流速度混沌特征参数的空间变化规律。

3.1 湍流速度信号的混沌特征参数空间分布规律

分别对设计工况下测线上测点的湍流速度信号的延迟时间、关联维数、Lyapunov指数和Kolmogrov熵进行计算，进一步拟合各条测线的混沌参数曲线，见图3，分别是设计工况下延迟时间个数、关联维数、Lyapunov指数和Kolmogrov熵的拟合曲线。其中，延迟时间为时间延迟个数与相邻时间序列点时间间隔的乘积。

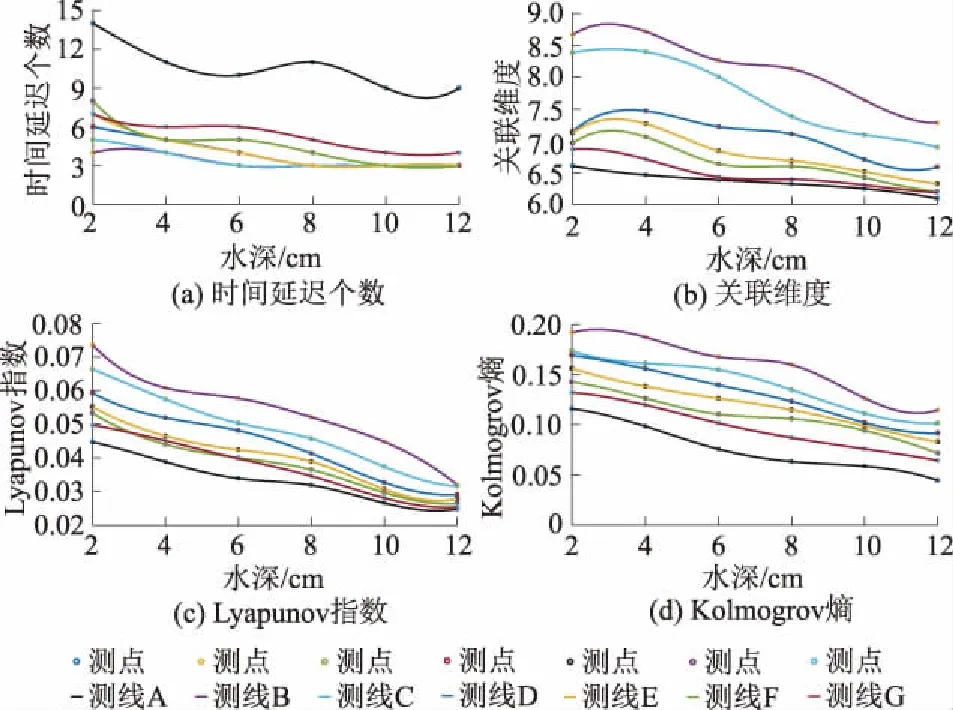
图3 沿程中垂线测点时间延迟个数、关联维度、Lyapunov指数、Kolmogrov熵

由图3(a)可知：各个测点的时间延迟个数分布在3～15之间；同一水深位置，测线A上各个测点的延迟时间均比其他测线测点的延迟时间要长。安装湍流控制板后，总体上看，同一水深，沿水流方向，测点的延迟时间依次增大；沿水深向上方向，测线上测点的延迟时间依次减小。这是由于安装湍流控制板后，在整体上，沿水深向上方向，随着湍流的发展，由于重力和自由水面的作用，垂直流速较小，限制了不同层水体的交换[26]，系统运动前后相关性不断减弱，使得湍流的时间过程行为反应敏感程度不断增强；沿水流方向，随着湍流的发展，在湍流控制板近壁区生成的湍流不断耗散和消亡，使得系统不断向稳态发展，湍流的时间过程行为反应敏感程度不断减弱，系统前后相关性不断增强。

由图3(b)—图3(d)可知：各个测点的关联维度、Lyapunov指数和Kolmogrov熵分别在6.094 9～8.661 7、0.024 8～0.073 6和0.044 2～0.191 8范围内，同一水深位置，测线A上各个测点的关联维度、Lyapunov指数、Kolmogrov熵比其他测线测点小。安装湍流控制板后，总体上看，同一水深，沿水流方向，测点的关联维度、Lyapunov指数、Kolmogrov熵依次减小；沿水深向上方向，测线上测点的关联维度、Lyapunov指数、Kolmogrov熵也依次减小。这是由于安装湍流控制板后，在湍流控制板近壁底区处，产生了涡量大、尺度小的涡结构，沿水流方向及水深向上方向不断衰减[27]，降低了湍流系统奇怪吸引子维数及其几何结构复杂程度，减少了湍流的混沌轨迹的局域不稳定性和初始条件敏感依赖性，削弱了湍流混沌系统的初始信息损失速率，从而使得测点的关联维度、Lyapunov指数和Kolmogrov熵沿水流方向和水深向上方向不断减小，湍流混沌强度不断减弱。

3.2 湍流速度信号的混沌特征参数及水力因子空间分布比较

一般而言，对于明渠水槽，湍流的雷诺数、紊动强度和相对紊动强度作为湍流统计平均的重要参数能够较好地反映湍流的一些特征。具体考虑到明渠水槽中，雷诺数与平均流速成正比，紊动强度是以脉动流速的均方根来反映紊动强弱的特征值，相对紊动强度是以脉动流速的均方根与相应时均流速的比值来反映紊动强弱的特征值。通过计算不同测点流向速度的平均流速、紊动强度和相对紊动强度，再分别与中垂面的空间位置拟合成空间曲面，见图4。进一步，在安装湍流控制板后，拟合出中垂面与各个混沌参数的空间曲面，见图5，分别为明渠水槽中垂面上时间延迟个数、关联维度、Lyapunov指数和Kolmogrov熵的拟合曲面。

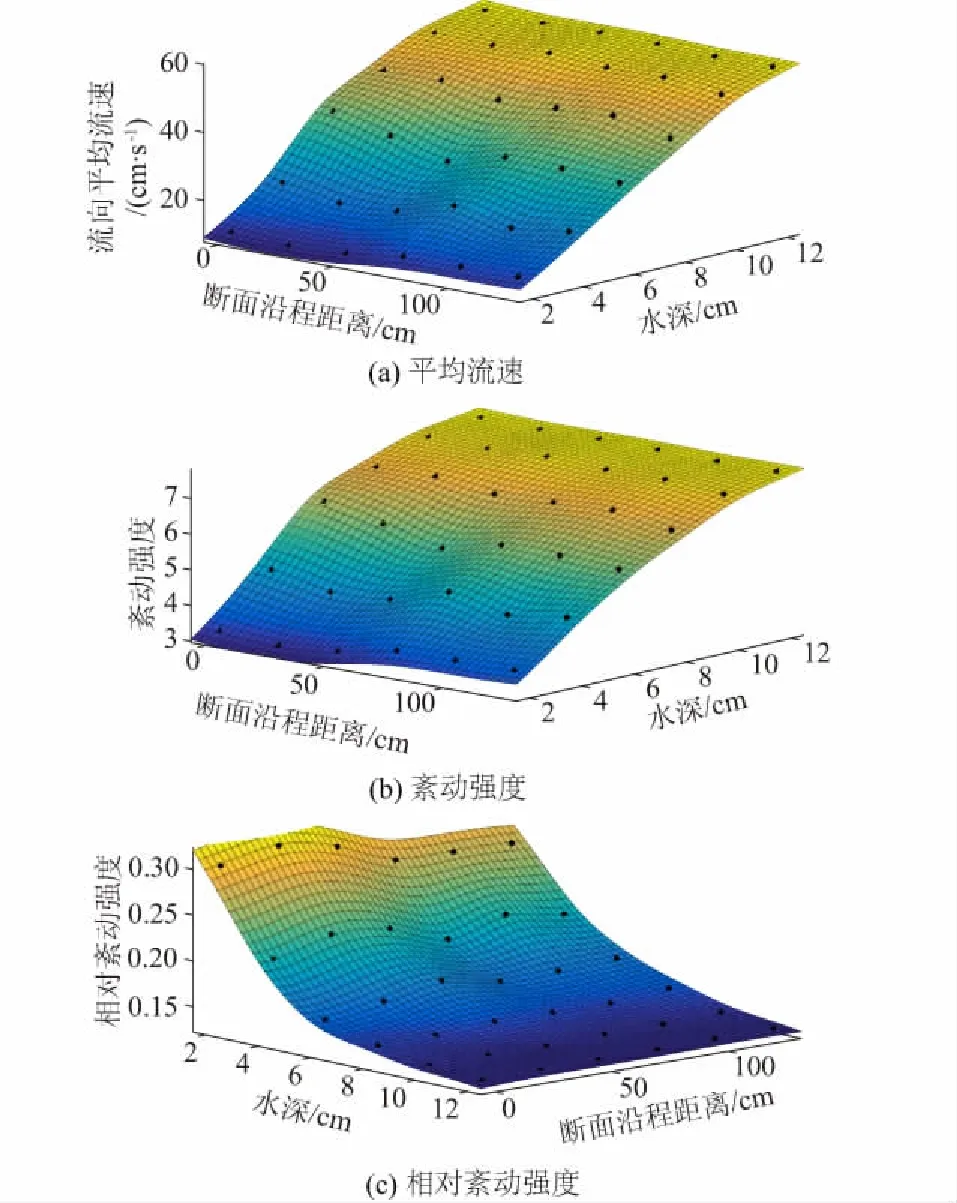
图4 沿程中垂面平均流速、紊动强度、相对紊动强度

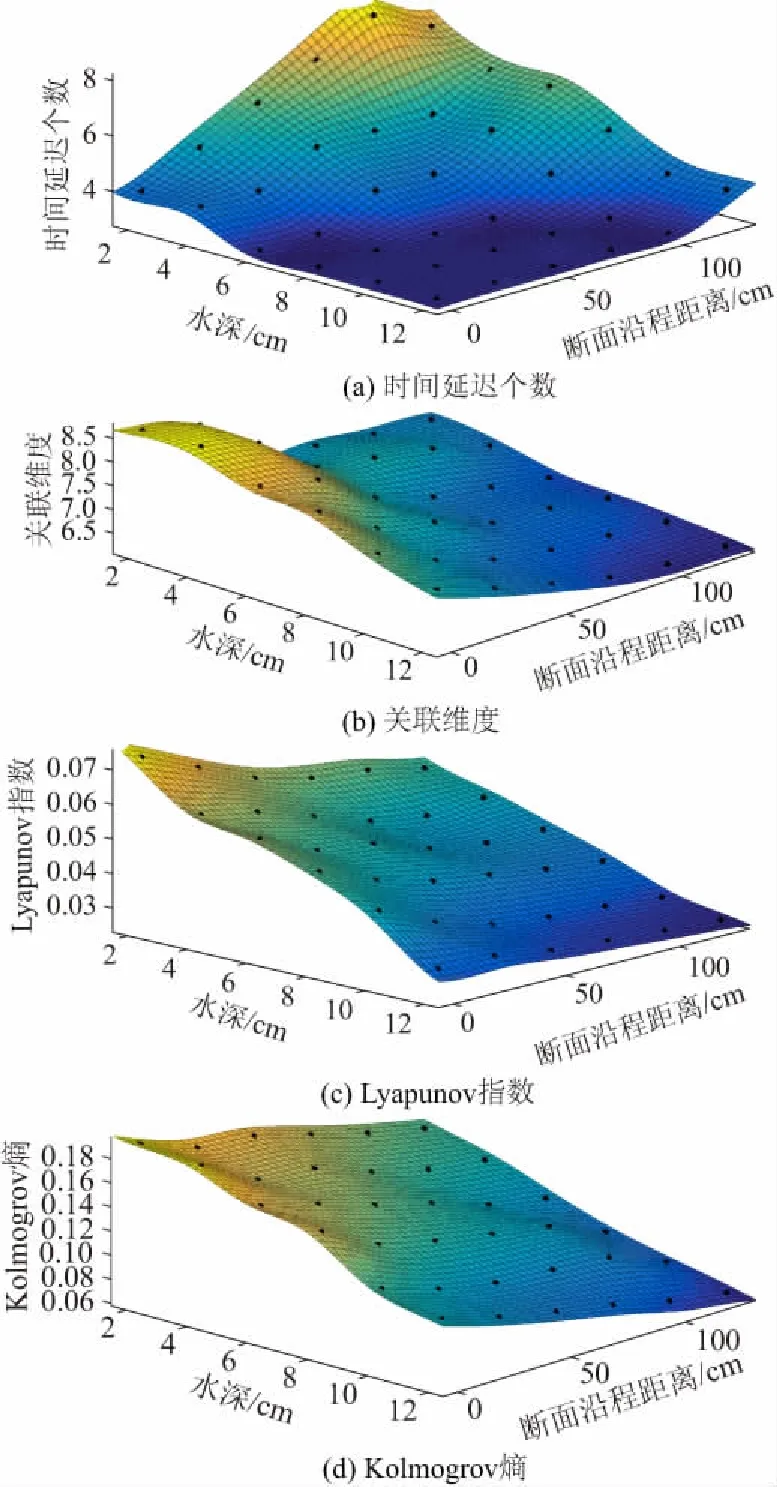
图5 沿程中垂面时间延迟个数、关联维度、Lyapunov指数、Kolmogrov熵

由图4(a)、图4(b)可知，安装湍流控制板后，测点流向平均流速和紊动强度分别在10.82～57.95 cm/s和3.17～7.61范围内。总体上看，同一测线上的测点的雷诺数和紊动强度沿水深向上方向不断增大；同一水深，沿水流方向，测点的雷诺数和紊动强度大小略微浮动，基本保持不变。

由图4(c)可知，安装湍流控制板后，测点流向相对紊动强度在0.13～0.32范围内。总体上看，同一测线上的测点的相对紊动强度沿水深向上方向不断减小；同一水深，沿水流方向，测点的相对紊动强度大小整体略微沿程减少，变化幅度微弱。

由图5可知：安装湍流控制板后，总体上看，沿水流方向，湍流速度的时间过程行为反应敏感程度沿程不断削弱；而沿水深向上方向，湍流速度的时间过程行为反应敏感程度不断增强；测点的关联维度、Lyapunov指数和Kolmogrov熵沿水流方向和水深向上方向不断减小。

综合图4、图5可知，安装湍流控制板后，由于上游来水在靠近湍流控制板近壁底区处与湍流控制板粗糙的表面摩擦，产生涡量大、尺度小的涡结构，沿水流方向及水深向上方向不断耗散与消亡。混沌特征参数在空间变化的规律能解释湍流涡结构沿水深及流向方向不断耗散和消亡的变化规律；而传统的水力因子，如雷诺数、紊动强度和相对紊动强度在沿水流方向涡结构不断耗散和消亡时，略微浮动，基本保持不变，无法解释湍流涡结构沿程耗散和消亡的变化趋势。