基于改进竞争威布尔模型的联合收割机可靠性评估研究

2019-12-21岳高峰曾百功

农机化研究 2019年3期

魏枭，岳高峰，柳剑，叶进，曾百功

(1.西南大学工程技术学院，重庆 400715；2.重庆市农业机械鉴定站，重庆永川 402160)

0 引言

随着农业联合收割机向多样化、复杂化、高参数化方向发展，其可靠性的问题越来越受到广大企业和用户的重视。维修成本高、可靠性差、故障频发是当前联合收割机进行农田工作过程中普遍存在的问题[1]。针对这些问题，国内外研究学者对联合收割机的故障数据分析与可靠性评估进行了一些研究。Dong Fang Hu等[2]提出利用有限元分析软件可更准确地计算联合收割机可靠性。Li Xiang Zhang等[3]利用FTA来定量分析联合收割机的可靠性，并找出其设计过程中的关键因素。王树文等[4]在基于RGA软件的稻麦联合收割机可靠性增长研究中指出应用RGA软件能够精确定量分析机械产品的可靠性。王艳芳等[5]建立起一种Bootstrap法与混合威布尔分布的可靠性评估模型并应用于农机产品的可靠性评估。梁明等[6]应用改进粒子群算法对收割机结构可靠性提出了优化算法。上述研究工作往往是将联合收割机的故障数据进行单一化处理，而不考虑使用故障数据的多种故障机理并存，即竞争性故障的客观存在；同时，由于不同故障对联合收割机的影响程度具有差异性，有些故障对联合收割机正常工作影响较小，即便出现这类故障，联合收割机也可带病工作，而有些故障则会使联合收割机功能严重破坏导致根本无法工作。因此，如果不对联合收割机使用故障数据采用新的计算分析方式，会导致联合收割机的可靠性计算结果出现不必要的误差，计算结果也并不符合联合收割机的实际使用情况。

本文利用联合收割机的使用故障数据，采用改进竞争威布尔模型对其可靠性进行评估，通过此模型可解决对故障机理单一化处理问题和不同使用故障对联合收割机影响差异性的问题。本文所提方法是对竞争威布尔理论的延伸与补充，可为联合收割机的可靠性评估提供了一条新的思路。

1 联合收割机使用故障模糊评判方法

1.1 故障特征属性和故障应力选择集的确定

目前，通常采用故障应力、故障机制和故障模式3个要素来描述故障[7]，然而由于机械系统的复杂性和这3个要素来表征故障的实用性有限，使单纯的故障机理分析变得异常困难[8]。因此，为完整表征联合收割机的故障特性和性质，本文定义其故障特征属性的概念如下：在联合收割机早期的使用故障期间内，其故障特征属性是造成使用故障产生的随机故障事件或最小随机故障事件的集合。记联合收割机的系统故障模式集合Fp(p=1,2,…,n)表示第p个系统故障模式，将故障模式Fp作为顶事件，使用故障树(FTA)进行分析，可以分析出对应n个造成故障模式Fp产生的最小割集fp1,fp2,…,fpn，即为故障模式Fp的故障特征属性。因此，故障模式Fp表示为

Fp=fp1，fp2，…，fpn

(1)

联合收割机是机电液一体化的复杂农业机械，包含多个子系统和多种零部件，工作时环境复杂且多变，故其承受多种复杂的故障应力，可归纳分为3大类：①联合收割机为了完成其基本作业功能所收到的应力，即为工作应力。②联合收割机工作时受到的环境应力，环境应力还应分为两种：一种是联合收割机在作业时外部环境作用于其上的应力；另一种是联合收割机工作时的内部应力即其内部各零部件之间的相互作用。③联合收割机由于人为原因导致不能正常使用，如人为操作不当造成的损坏或者不能正常工作等问题。通过结合联合收割机的实际工作情况及外部环境等因素，确定其故障应力选择集为

S={S1,S2,S3,S4,S5,S6}={工作应力，内部应力，

工作环境作用应力，偶然因素，人为因素}

1.2 建立故障与故障应力之间的关系

(2)

设有g个故障应力共同激发一个fpi，请专家逐次对g个故障应力进行两两比对，评出两者中最容易激发故障特征属性产生的故障应力，可能性大者的记为一次，得到g个故障应力各自的出现次数t1,t2, …,tg。依据评定出的结果，用故障应力累计次数最多的总次数为分母，去除其他应力的累计次数,公式为

(3)

1.3 联合收割机故障特征属性权重的确定

(4)

其中，aij表示的是故障特征属性i与故障特征属性j对故障模式的重要度。

表1 模糊评判标度表

(5)

利用式(5)可得到故障特征属性fp1,…,fpn的权重：Wp=(wp1,…,wpi,…,wpn)。其中，wpi为

(6)

其中，β是权重分配的分辨率参数。同理，可求得联合收割机的系统故障模式F1,…,Fp,…,Fl的权重W=(W1,W2,…,Wl)。根据联合收割机各系统故障特征属性的权重和模糊关系矩阵可得到联合收割机的单系统故障模糊评判公式为

(7)

其中，bpi表示的是联合收割机的故障模式Fp对其故障应力选择集中si的判断值。其数值越大表示故障应力si对故障模式Fp激发效果越明显。即可得到联合收割机全系统故障模糊综合评判公式为

(8)

2 使用故障数据处理和可靠性评估模型

可靠性评估是分析评价产品可靠性水平的重要方法，而威布尔分布是描述零部件与复杂机械系统寿命分布规律的一种最常见分布形式[11]。对于联合收割机而言，使用故障数据是非独立同分布，说明单威布尔模型并不符合联合收割机的可靠性评估要求。尚永爽等[12]根据故障竞争性故障装备对竞争威布尔模型和混合威布尔进行了分析。由于混合威布尔模型中的子分布对数据要求为连续的顺序统计量，这明显不符合联合收割机多种竞争性故障机制的寿命过程[13]。联合收割机可靠性评估过程中忽略故障机制的差异性，用单一化模型拟合全部使用故障数据是其他威布尔模型最显著的缺陷，而本文通过改进竞争威布尔模型来评估可靠性的正是对这一严重缺陷的弥补。

2.1 故障数据统计分析与故障影响等级评级标准

本文对10台重庆市某国产联合收割机的使用状况进行跟踪并收集相应使用故障数据，跟踪期间共统计发生13类故障。根据联合收割机自身特点和实际使用情况，参考《农业机械设计手册》和之前对联合收割机所做的研究，对使用故障数据进行统计分析，对各类故障进行分析评级，故障影响等级评级标准如表2所示。按照该标准，得到联合收割机13类故障模式集的故障特征属性与故障影响等级，如表3所示。

表2 故障影响等级评级标准

表3 联合收割机故障模式集、故障特征属性和故障影响等级

续表3

2.2 基于改进竞争威布尔的可靠性评估模型

竞争威布尔模型的适用条件[14]为：①建模对象应该是系统组成要素的寿命长度，即建模对象是使用故障发生时间；②系统中每个要素寿命必须是独立同分布的，即要素故障机制必须相同或相似。

联合收割机基于改进竞争威布尔模型的失效分布函数为

(9)

通过故障模糊聚类将使用故障集归成m类，每类使用故障集对应一个相似或相同的且独立作用于联合收割机的故障机制，即T=Min{T1,T2,…,Tm}。设Fi(t)是Ti的累积失效分布函数，因此可得到联合收割机全系统的累积失效分布函数为

(10)

其中，Fi(t)可以为不同的失效分布函数，但这m个失效分布函数应都具有独立性。

联合收割机的系统故障率为

(11)

其中，λi(t)表示的是联合收割机第i类使用故障的改进竞争威布尔分布失效率。

其对应的可靠度为

(12)

2.3 故障信息序列的表达方式

本文对不同类型的使用故障进行专家评级，最终将每个使用故障分到4个等级中并赋予每个故障等级相应的权重为Z={Z1致命、Z2严重、Z3一般、Z4轻微}={1、0.7、0.4、0.1}。故障应力是引发使用故障发生的条件，故障机制是故障应力开始发生作用直至引起使用故障的静态或动态的过程[15]。根据联合收割机的故障应力相似性来表示其故障机制的相似性，应用前文提到模糊评判的方法，使用故障影响等级和故障特征属性集合对故障应力的模糊评判结果进行处理分析，以此作为故障信息序列。

联合收割机系统故障模式Fp={fp1,fp2,…,fpn}的故障信息序列为

(13)

2.4 使用故障数据的模糊聚类分析

通过联合收割机的故障信息序列来表示其系统的使用故障，故障聚类对象是故障信息序列的集合{B1,B2,…,Bn}。其中，Bi都是由一组(bi1,bi2,…,big)构成的。依据联合收割机系统故障信息相似程度来建立使用故障模糊相似矩阵A=(aij)n×n。其中，aij表示故障Bi与Bj的相似度，其计算公式为

(14)

用上述方法建立的使用故障模糊相似矩阵A只具有自反性和对称性，但并不符合传递性的需求，因此需要求出使用故障模糊相似矩阵的传递闭包t(A)。从传递矩阵A开始计算，应用平方法逐次求出A→A2→A3→…→AK，直到首次得到AK=A2K，AK就是A的传递闭包t(A)，计算方法为

A4=A3∘A

⋮

(15)

3 威布尔模型参数估计

3.1 自助抽样法(Bootstrap)

自助抽样法(Bootstrap)是美国Stanford大学的统计学教授Efron最先提出的一种数据再抽样统计方法。其原理是将初始数据通过再抽样的方法获得数量相同的自助样本，然后用观察分析统计量与自助统计量的关系去逼近观察统计量与真实值之间的关系[16]。

自助抽样法通常用于下列情况：①初始的标准假设无效；②需要解决复杂问题，但没有理论依据。

自助抽样法的基本思想是通过再抽样和自助分布等方法，自助分布不但包含初始总体数据的全部信息，而且还包含了之后统计量抽样分布的信息[17]。大多数情况下，自助分布的形状接近于样本分布的形状[18]。自助抽样法不需要用中心极限定理或者其他理论，可以通过计算机模拟毫不费力地获得大量自助样本，再通过自助样本对总体进行评估。

3.2 改进竞争威布尔模型参数的计算方法

利用自助法对改进竞争威布尔模型参数进行估计计算的具体步骤如下：

1)改进竞争威布尔模型分布函数的线性化。

根据改进竞争威布尔失效分布函数式(9)可得

(16)

对式(16)两边同时取两次对数，可得到

(17)

(18)

2)根据原始数据利用线性化模型(18)计算出参数a和b的估计值，即

(19)

(20)

3)由式(18)得出离差，即

(21)

4)以离差ei作为初始数据，应用bootstrap法进行数据再抽样，生成500个自助样本。

6)由式(19)、式(20)得出每个自助重复中参数a、b的估计值。

7)由a=-βlnη和b=β，计算得出β、η的再抽样分布。

8)通过计算可得出参数η、β的点估计值和区间估计范围。

4 算例分析

为了体现本文计算过程的科学性和普遍性，故从收集到的某国产联合收割机某次试验的使用故障数据中抽选8类故障模式(4种故障等级中每种选2个)进行可靠性分析计算，算例分析结果如下：取故障集为F={F1上割台不能正常升降、F2发动机启动后自动行走、F3割刀往复运动停止、F4刮板严重变形或损坏、F5机身支架或挡板断裂、F6扶禾无力或扶禾器不转动、F7谷物未脱净、F8脱粒盖排草口处农作物损失率过大}。故障时间为T={266h、307h、404h、469h、521h、593h、675h、792h}，依据本文介绍的方法对联合收割机的各故障模式进行故障树(FTA)分析，得到相应故障特征属性集合，依据专业知识及模糊推理的方法可得到联合收割机全系统故障对其故障应力选择集模糊综合评判模型。计算结果为

根据模糊聚类的方法，计算聚类阈值λ为1、0.987 3、0.957 4、0.947 2、0.927 5、0.923 2、0.898 2、0.898 1，并且阈值越大分类数越多。取λ=0.923 2和λ=0.898 2进行计算，得到等价关系矩阵为

由此可以将故障数据集分为{t1,t2,t3,t4,t5,t8}，{t6}，{t7}3类和{t1,t2,t3,t4,t5,t8}，{t6,t7}两类，考虑到计算时需要对小样本数据进行处理的要求，故选择λ=0.898 2来作为使用故障数据集的聚类结果。即取λ=0.898 2的聚类结果作为改进竞争威布尔模型中两个独立分布的使用故障数据，分别为T1={266h、307h、404h、469h、521h、792h}和T2={593h,675h}。由第3节介绍的方法可以得出η1、β1与η2、β2的点估计值和区间估计范围，改进竞争威布尔和单威布尔的对应参数计算结果如表4所示。

联合收割机基于改进竞争威布尔模型的故障率为

4.1456×10-6t0.8095+1.3842×10-9t2.4298

表4 改进竞争威布尔和单威布尔参数估计值

联合收割机基于改进竞争威布尔模型的可靠度函数为

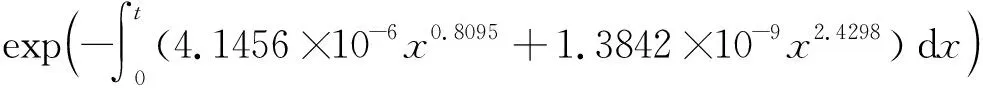
=exp-2.2902×10-6t1.8095-0.4036×10-9t3.4298

联合收割机基于改进竞争威布尔模型的失效密度函数为

4.1456×10-6t0.8095+1.3842×10-9t2.4298·
exp(-2.2902×10-6t1.8095-0.4036×10-9t3.4298)

改进竞争威布尔模型和单威布尔模型计算出的可靠度函数图像对比如图1所示。图1中，实线为改进竞争威布尔模型的可靠度函数曲线，虚线为单威布尔模型可靠度函数曲线。对比二者图像可以看出：通过改进竞争威布尔模型计算出的可靠度函数结果的整个曲线都在单威布尔模型计算结果的下方，这是由于本文为了减小计算结果与联合收割机实际使用情况的误差对使用故障数据进行了分类化处理和模糊聚类分析；改进竞争威布尔模型的可靠度函数计算结果与单威布尔模型的计算结果出现显著差异，这是由于联合收割机在工作一段时间后出现的一些使用故障严重影响联合收割机正常工作，同时考虑到联合收割机使用故障的复杂性和故障机制的多样化，因此会使改进竞争威布尔模型的计算结果与单威布尔模型的计算结果差异显著增加。考虑到联合收割机竞争性故障的客观存在、不同使用故障对联合收割机影响程度的差异性和“用户可靠性感受明显低于评估结果”的现象，笔者认为本文通过改进竞争威布尔模型可靠度计算结果是合理的且更符合实际情况。