基于IDA的高速铁路大跨度斜拉桥地震易损性分析

周岳武　符云集　颜璐　赵晓苗　万克成

摘  要：为研究高速铁路大跨度斜拉桥的地震易损性，以我国西部某主桥跨径为249.5m+550m+550m+249.5m的三塔四跨铁路斜拉桥为研究对象，利用有限元软件SAP2000建立其动力有限元分析模型，采用增量动力分析（IDA）获得结构地震响应，结合对数回归分析最终获得各关键构件的地震易损性曲线。结果表明：二次拟合得到的概率地震需求模型整体略优于一次拟合;在纵向地震作用下，支座呈现出较高的损伤概率，其中固定支座损伤概率最大;桥塔和桥墩的损伤相对较低。因此在大跨度铁路斜拉桥抗震设计中，应重点考虑位移和变形的控制。

关键词：高速铁路大跨度斜拉桥;增量动力分析;地震需求模型;易损性曲线

中图分类号：U441.3 文献标志码：A 文章编号：2095-2945（2019）34-0001-05

Abstract： In order to study the seismic vulnerability of high-speed railway long-span cable-stayed bridge， a three-tower and four-span railway cable-stayed bridge with a main bridge span of 249.5m+550m+550m+249.5m in western China is taken as the research object， and its dynamic finite element analysis model is established by using finite element software SAP2000. The seismic response of the structure is obtained by incremental dynamic analysis （IDA）， and the seismic vulnerability curve of each key component is obtained by logarithmic regression analysis. The results show that the probabilistic seismic demand model obtained by quadratic fitting is slightly better than the first fitting， and the bearing presents a higher damage probability under the action of longitudinal earthquake， in which the damage probability of fixed bearing is the highest. The damage of bridge tower and pier is relatively low. Therefore， the control of displacement and deformation should be considered in the seismic design of long-span railway cable-stayed bridge.

Keywords： high-speed railway long-span cable-stayed bridge; incremental dynamic analysis; seismic demand model; vulnerability curve

1 概述

近年来，随着我国开始加大西部地区建设力度，许多跨越山谷的铁路桥梁被建造，具有良好跨越能力的斜拉桥越来越受关注[1]。而我国西部地区处于地震多发带，且目前国内外有关斜拉桥的抗震性能的研究成果大多集中于公路常规斜拉桥[2]，徐凯燕等[3]对武汉军山长江大桥进行一致激励和非一致激励下的抗震性能分析;庞于涛、袁万城等以某斜拉桥主塔为研究对象，考虑混凝土和钢筋随时间的劣变时效，采用神经网络和蒙特卡洛方法对桥梁易损性展开研究[4];夏修身等[5-6]通过增量动力分析探讨了大跨双塔斜拉桥桥塔的非线性抗震性能。以上研究大多是针对公路斜拉桥进行展开，对于高速铁路大跨度斜拉桥抗震性能研究仍很欠缺，因此，有必要对此类桥梁的抗震性能展开系统分析，从而确保该类桥梁在地震作用下的安全。

因此，本文以我国西部某三塔四跨高速铁路大跨度斜拉桥为研究对象，从基于性能的抗震设计思想，深入分析概率地震需求分析模型，构件损伤概率，进而获得桥梁整体损伤规律，以期为该类桥梁的抗震设计、抗震性能评估和地震灾害预防提供理论参考。

2 桥梁分析模型建立

2.1 桥梁工程概况

西部某高速铁路大跨度斜拉桥主桥跨径布置采用249.5m+550m+550m+249.5m，主桥墩塔编号从左到右依次为1#～7#，其中3#～5#为主塔，2#、6#为两侧辅助墩，1#为过渡墩，7#为桥台，如图1所示。主桥主梁断面采用“工”字型边主梁。主塔在横桥向的形式为“钻石”型，在纵桥向的形式为四肢空心薄壁。全桥共设264根斜拉索，按扇形布置。主桥支座布置如图2所示。

桥址场地基本烈度为Ⅵ度，设计基本加速度为0.05g，特征周期为0.35s，场地类别为II类。

2.2 桥梁有限元模型

利用SAP2000有限元软件建立某铁路斜拉桥大桥全桥有限元模型，为方便计算，对斜拉桥模型进行合理的简化。主梁、主塔及桥墩用空间梁单元进行模拟，桥面板用板单元进行模拟，斜拉索用拉索单元进行模拟，同时进行弹性模量修正并考虑索力的P-Δ效应。主梁采用双主纵梁模型，并采用模拟实际尺寸的横梁和小纵梁进行连接，从而形成空间梁格;桥面轨道铺装等作为二期恒载考虑，并将其转化为质量;本模型在建立时考虑了桩-土-结构的相互作用，采用m法计算出承台底的桩-土弹簧作用，并用6×6矩阵模拟;同时建立了一联引桥作为主桥一侧的边界条件，另一侧边界条件为桥台;且所有支座按照该铁路斜拉桥成桥状态的实际情況采用连接单元模拟。建成的三维有限元模型见图3，结构第一阶自振频率0.161s-1，振型形状为主梁一阶耦合反对称竖弯+纵飘，3#、4#、5#主塔同步顺桥向振动;结构第二阶自振频率0.259s-1，振型形状为主梁二阶反对称竖弯+纵飘，3#和5#塔同步顺桥向振动;结构第三阶自振频率0.273s-1，振型形状为主梁一阶正对称侧弯，3#、4#、5#主塔同步侧弯。

3 概率地震需求分析

3.1 地震动记录的选取

本文首先计算桥址处的设计反应谱并作为目标谱，然后从太平洋地震研究中心（PEER）中选取平均反应谱与目标反应谱匹配最好的20条实际地震动记录作为地震输入，如图4所示。最后，将其地面峰值加速度（PGA）调幅为0.05g、0.1g、0.2g、0.4g、0.8g，共生成100条地震动，这里地震动的输入考虑竖向地震动的影响，输入方式采用纵向+竖向地震组合，竖向加速度值取2/3的水平向加速度值。

3.2 概率地震需求分析

基于IDA获得100个不同结构关键部位的地震响应，然后通过对数回归分析获取桥梁不同结构关键部位的地震需求模型。

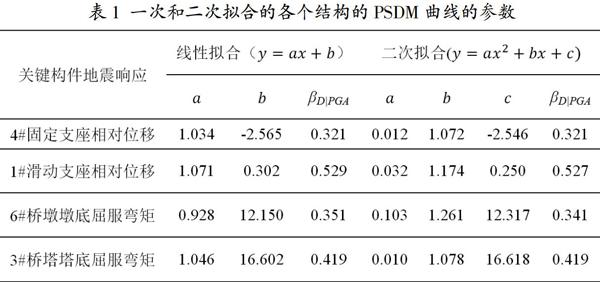
在本文分析中，以PGA作为地震动强度指标，地震需求为各个结构损伤指标在地震下的峰值响应，采用一次和二次回归获得该铁路斜拉桥的桥塔、支座、桥墩关键截面的概率地震需求模型与相关参数如图5和表1所示。

从图5和表1中可以看出桥塔、支座结构地震概率需求模型的一次拟合与二次拟合基本一致，而桥墩地震概率需求模型的一次拟合与二次拟合有一定区别。能够看出二次拟合得到的需求模型比一次拟合的拟合度要更高。

4 地震易损性分析

4.1 铁路斜拉桥结构易损性曲线

结构地震易损性分析指的是在特定强度水平地震动作用下结构响应超越结构损伤状态所表示的结构承载能力的条件概率。结构的地震易损性模型可以利用地震需求D与结构的抗震能力C的比值不大于1来定义，即用下式表示：

由于地震需求D与结构抗震能力C都服从对数正态分布，因此能够得出结构地震易损性计算模型为：

式中，mD为桥梁结构抗震需求中位值，mC为桥梁结构抗震能力中位值，当选取PGA作为地震动参数时，取0.5。

4.2 损伤指标选取与量化

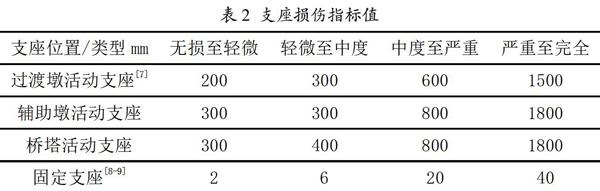
结构的地震损伤指标是一个无量纲指数，用来评价结构及其构件在地震作用后的破坏状态。国内外很多专家对于损伤指标的选取和量化做了许多研究，目前仍没有普遍适用的指标。此处采用公路斜拉桥分析中较为成熟的指标：位移、轴力比、曲率、曲率延性比等。

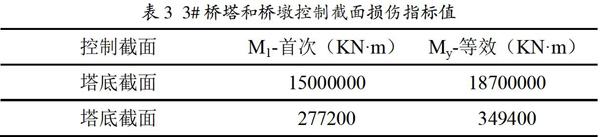
桥塔和桥墩采用屈服弯矩作为损伤指标[10-11]，通过研究弯矩随截面曲率的变化关系来确定使截面发生首次屈服与等效屈服的首次弯矩M1和等效弯矩My，主要控制截面（底截面）量化取值见表3。

根据拟合所得的铁路桥梁结构概率需求回归模型与量化的各个结构的损伤指标，可以计算铁路斜拉桥各个结构关键截面在不同损伤状态下对应的损伤概率，从而得到相应的易损性曲线，如图6所示。

分析图6，可知在纵向地震作用下支座相较于桥墩和桥塔更容易发生破坏，且固定支座比滑动支座更易发生破坏。PGA=0.1g时，固定支座一定发生轻微破坏，60%发生中度破坏，不太可能发生严重破坏，PGA>0.2g时，才值得考虑固定支座的严重破坏;PGA<0.2g时，基本不用考虑滑动支座的破坏;PGA=1.0g时，6#桥墩墩底首次屈服的概率未超过40%，说明结构具有很好抗震性能;PGA<0.4g时，桥塔塔底不会发生屈服，PGA=1.0g时，首次屈服的概率未超过60%，说明结构具有很好抗震性能。因此在大跨度铁路斜拉桥抗震設计中，应重点考虑支座位移和变形的控制。

5 结论

本文基于IDA分析方法构造易损性曲线对某三塔四跨高速铁路大跨度斜拉桥进行地震易损性分析得到以下结论：

（1）采用二次回归拟合得到的概率地震需求分析模型整体略优于一次线性拟合，故建议采用二次拟合来得到该类斜拉桥的地震需求概率模型。

（2）在纵桥向地震作用下，支座系统的损伤概率总体较大，而桥墩和桥塔损伤概率相对较低。

（3）该类斜拉桥结构的抗震设计中，控制位移较控制结构内力更加关键。

参考文献：

[1]王克海.桥梁抗震研究[M].北京：中国铁道出版社，2014：56-100.

[2]赵人达，许智强，邹建波，等.基于ANSYS的大跨斜拉桥地震响应分析及性能评估[J].建筑科学与工程学报，2018，35（4）：19-26.

[3]杨得海，郭镇，李小珍.大跨度铁路斜拉桥地震易损性分析[A].2019年世界交通运输大会论文集[C].2019：8.

[4]徐凯燕，魏德敏.武汉军山长江大桥非线性地震反应时程分析[J].湖南大学学报（自然科学版），2010，37（5）：19-23.

[5]庞于涛，袁万城，党新志，等.考虑材料劣变过程的桥梁地震易损性分析[J].同济大学学报（自然科学版），2013，41（3）：348-354.

[6]夏修身，李建中，管仲国，等.斜拉桥桥塔非线性抗震性能研究[J].中国公路学报，2016，29（3）：66-72，81.

[7]GUPTA A，KRAWINKLER H. Estimation of seismic Drift Demands for Frame Structures[J]. Earthquake Engineering Structural Dynamics，2000，29（9）：1287-1305.

[8]李立峰，吴文朋，黄佳梅，等.板式橡胶支座地震易损性分析[J]. 湖南大学学报（自然版），2011，38（11）：1-6.

[9]Mander JB， Kim DK， Chen SS， Premus GJ. Response of steel bridge bearings to the reversed cyclic loading[R]. Tech Report NCEER96-0014， Buffalo（NY）， 1996.

[10]Randall MJ， Saiidi MS， Maragakis EM， Isakovic T. Restrainer design procedures for multi-span simply supported bridges[R]. Tech Report MCEER-99-0011， 1999.

[11]Pan Y， Agrawal A K， Ghosn M. Seismic Fragility of Continuous Steel Highway Bridges in New York State[J]. Journal of Bridge Engineering， 2007， 12（6）：68-69.

[12]冯清海.特大桥梁地震易损性与风险概率分析[D].同济大学，2008.