基于复阻尼模型的改进时域计算方法

孙攀旭　杨红　刘庆林

摘   要：針对复阻尼运动方程自由振动解中存在发散项，导致其不可计算结构自由振动响应，同时基于复阻尼模型的时域计算结果不能稳定收敛的问题，在复阻尼模型的基础上，利用时频域转换得到改进时域运动方程;引入地震加速度在时间步长内是线性变化的假定，利用改进时域运动方程的特点，提出地震作用下基于复阻尼模型的改进时域计算方法.算例分析表明：相比复阻尼模型的时域运动方程，改进的时域方程可适用于结构自由振动响应的时域计算，且计算得到的地震作用下结构动力响应是稳定收敛的;相比基于改进时域运动方程的傅里叶级数法，本文提出的改进时域计算方法计算量更少，计算效率更高. 随着阻尼比的增大，复阻尼模型的改进时域方法和黏性阻尼模型的时域方法计算结果差异逐渐增大.当结构阻尼比为0.5时，在部分地震波作用下两种方法计算得到的加速度峰值相对误差可达到20%以上.

关键词：复阻尼;改进;地震作用;时域;黏性阻尼

中图分类号：TU311.3                           文献标志码：A

Improved Time Domain Calculation Method Based

on Complex Damping Model

SUN Panxu1，YANG Hong1，2，LIU Qinglin3

（1. School of Civil Engineering，Chongqing University，Chongqing 400045，China;

2. Key Laboratory of New Technology for Construction of Cities in Mountain Area

of the Ministry of Education，Chongqing University，Chongqing 400045，China;

3. School of Traffic and Engineering，Shenzhen Institute of Information Technology，Shenzhen 518172，China）

Abstract：There are divergent items in the free vibration solution of complex damping vibration equation. The structural free vibration responses cannot be calculated based on complex damping model， and the structural time domain calculation results are not stably convergent. On the basis of the complex damping model， the improved time domain motion equation can be obtained by time and frequency domain transformation. In the time step， it is assumed that the relationship of earthquake acceleration is linear. By the characteristics of the improved motion equation， the improved time domain calculation method under earthquake action is put forward. The cases show that， compared with the time domain motion equation of complex damping model， the improved time domain motion equation can be applied to the time domain calculation of structural free vibration responses. The structural time domain calculation results are stably convergent under earthquake action. Compared with the Fourier series method， the calculation amount of the proposed method is less and the computational efficiency of the proposed method is higher. With the increase of damping ratio， the difference between the improved time domain calculation method of complex damping model and the time domain calculation method of viscous damping model is increasing gradually. When the damping ratio is 0.5， the biggest relative error of structural acceleration peak values which are calculated by the two methods is over 20% under some seismic wave.

Key words：complex damping;improved;earthquake action;time domain;viscous damping

在结构动力计算中，基于黏性阻尼模型的Rayleigh阻尼模型由于数学处理的便利性得到了广泛应用[1]，但Rayleigh阻尼模型的计算结果与所选取的控制频率有关，其合理性不易被判定[2]. 相比黏性阻尼模型，复阻尼模型的计算结果仅依赖于结构材料的阻尼特性，不受结构自振频率组合选择的影响，计算结果的合理性易被判定[3]. 复阻尼模型认为阻尼力与位移成正比，且滞后一个相位角，在稳态简谐振动中得到每周耗能与频率无关，但其运动方程的自由振动解存在发散项[4]. 朱敏[5]、李鹏[6]等采用常平均加速度法对复阻尼方程求解;潘玉华等[7]采用高斯精细时程积分法求解复阻尼运动方程;张辉东等[8]采用 积分法研究了复阻尼模型结构弹性时程响应，由于复阻尼模型时域运动方程通解中存在发散项，导致上述方法的计算结果存在不稳定性;朱镜清等[9-10]舍弃通解中发散项的计算方法，虽然保证了计算结果的稳定性，但是在数学上是不正确的[11].为消除不稳定问题，部分学者对复阻尼运动方程进行改进，或依据新阻尼模型构建运动方程. Reggio等[12]将Maxwell-Wiechert本构模型等效于复阻尼本构模型;周正华等[13]采用Maxwell-Kelvin型本构逼近复阻尼本构;Wang[14]采用Rayleigh阻尼矩阵等效复阻尼矩阵;Lee等[15]将黏性阻尼理论与复阻尼模型相结合;尚守平等[16]提出阻尼力与加速度成正比，进而得到新的运动方程;Pan等[17]研究了卷积型阻尼运动方程的构建和求解，但上述方法得到的计算结果与复阻尼模型存在一定的誤差.

针对复阻尼模型自由振动解中包含发散项的问题，本文在不改变复阻尼模型的物理本质基础上，利用时频域转换原则，得到复阻尼模型的改进时域运动方程表达式，使得自由振动解中不再含有指数增长项，从而实现自由振动响应的时域计算;依据运动方程的特点，引入地震加速度在时间步长内是线性变化的假定，进一步提出了复阻尼模型的改进时域计算方法，可计算地震作用下结构的动力响应.

1   复阻尼模型的改进时域计算方法

1.1   复阻尼模型的改进时域运动方程

基于复阻尼模型的时域自由运动方程为：

式中：η为损耗因子;i为虚数单位，即i = ;ω为结构的无阻尼自由振动频率，即ω = .

方程（1）对应的特征方程为：

令λ =  χ + iδ，则：

依据式（3），可知方程（1）的通解实部为：

由χ2 > 0，可知式（4）右边项中包含有指数增长项，即发散项，因此基于复阻尼模型的时域自由运动方程为病态方程，通解中包含有发散项，导致复阻尼模型无法计算自由振动响应.

针对复阻尼模型的缺陷，对其进行改进.地震作用下基于复阻尼模型的单自由度体系时域运动方程为：

式中：g（t）为地震加速度，利用复化对偶原则[18]可得到g′（t）.

对方程（5）进行傅里叶变换，可得：

式中：为振动频率;（i）为x（t）的傅里叶变换;

G（i）为g（t）的傅里叶变换.

振动频率不为零时，方程（6）进一步转化为：

对方程（7）进行傅里叶逆变换，可得复阻尼模型的改进时域运动方程为：

方程（8）在实数域中的表达式为：

1.2   结构的自由振动响应

方程（9）对应的自由振动方程为：

采用复平面法求解方程（10），假定其解为：

x（t） = Ae     （11）

由式（11）可得到结构的振动频率为：

= α     （12）

由式（11）可得：

（t） = i（α + iβ）Ae（t） = -（α + iβ）2Ae        （13）

将式（11）和式（13）代入方程（10），得：

-（α + iβ）2 + i（α + iβ） + ω2 = 0     （14）

式（14）进一步转化为：

-α2 + β2 - β + ω2 = 0-2αβ + α = 0        （15）

求解方程（15），可得：

α1=ω，β1=α2=-ω，β2=

（16）

自由振动响应的表达式为：

x（t） = [C1cos（f t） + C2sin（f t）]e    （17）

其中：

C1 = x（t0）C2 = f  =    （18）

式（17）中不包含发散项，因此复阻尼模型的改进时域方程可计算结构的自由振动响应.

1.3   地震作用下结构的动力响应

对于复阻尼模型的改进时域运动方程，考虑到阻尼项中包含有结构的振动频率，而结构的振动频率为未知项，因此传统的常平均加速度法、 Newmark-β法等时程计算方法不能直接用于其时域计算.

将时间离散化，按照时间步长Δt对时间进行离散，任意时刻可表示为tk = kΔt（k = 0，1，2，…）. 谢礼立等[19-20]提出了基于黏性阻尼模型的时域精确法，用于计算地震作用下结构的动力响应，假定地震加速度在时间步长内是线性变化的，以tk时刻的位移和速度作为初值，计算tk+1时刻的位移、速度和加速度，进而完成时域数值计算.本文引入地震加速度在时间步长内是线性变化的假定，在tk时刻到tk+1时刻，地震加速度可表示为：

g（t） = g（tk） + （t - tk）   （19）

依据式（19），tk时刻到tk+1时刻，地震作用下基于复阻尼模型的改进时域运动方程可进一步表示为：

（）+（）+ω2x（）=

-g（tk）-   （20）

其中，

= 0，t = tkΔt，t = tk+1    （21）

方程（20）对应的齐次方程通解与自由振动解形式相同，即：

xc（） = e[C1sin（f ） + C2cos（f ）]    （22）

求解方程（20）的特解时，考虑到地震加速度在时间步长内是线性变化的，没有振动频率，因此结构在每个时间步长内仅含有一种振动频率，即有阻尼自由振动频率，可得：

= f  =     （23）

假定结构的特解为：

xp（） = a + b    （24）

由式（24）可得：

p（） = ap（） = 0    （25）

将式（23）～（25）代入方程（20）可得：

a+ω2（a+b）=-g（tk）-   （26）

求解方程（26），可得：

a = -b =  -     （27）

方程（20）的特解为：

xp（t） = - + -

（28）

由式（22）和（28）得到方程（20）的通解為：

x（） = e[C1sin（f ）+C2cos（f ）] -+

-

（29）

（） = e[C1f cos（f ）-C2f sin（f ）] +

（-）e[C1 sin（f ）+C2 cos（f ）] -

（30）

进一步计算出tk+1时刻的位移、速度和加速度为：

x（tk+1）=e[C1sin（f Δt）+C2cos（f Δt）] -+

-

（31）

（tk+1） = e[C1f cos（f Δt）-C2f sin（f Δt）] +

（-）e[C1 sin（f Δt）+C2 cos（f Δt）] -

（32）

（tk+1） = e[-C1f2 sin（f Δt）-C2f2 cos（f Δt）] +

2（-）e[C1f cos（f Δt）-C2 f sin（f Δt）]×

（-）2e[C1 sin（f Δt）+C2 cos（f Δt）]

（33）

其中：

C1=[x（tk）+（tk）-+     g（tk）+] C2=x（tk）-+

（34）

依据式（31）～（34），由tk时刻结构的x（tk）和

（tk），可计算出tk+1时刻x（tk+1）、（tk+1）和（tk+1），从而实现基于复阻尼模型的改进时域计算方法.

2   复阻尼模型的改进时域计算方法验证分析

2.1   自由振动响应的验证分析

以结构自振频率为4 rad/s的单自由度体系为例，分别构建模型A、模型B、模型C和模型D，4种模型仅阻尼比不同. 模型A的阻尼比ξ = 0.02，损耗因子η = 2ξ = 0.04[3];模型B的阻尼比ξ = 0.05，损耗因子η = 2ξ = 0.10;模型C的阻尼比ξ = 0.10，损耗因子η = 2ξ = 0.20;模型D的阻尼比ξ = 0.20，损耗因子η = 2ξ = 0.40. 4种模型的初始位移为10 cm，初始速度为10 cm/s，利用本文方法计算其自由振动响应，所得结果如图1所示.相比复阻尼模型的时域运动方程，改进的时域运动方程可计算自由振动响应，不存在发散现象.随着阻尼比的增加，结构自由振动响应的收敛速度增大，与实际相符.

2.2   地震作用下的动力响应验证分析

目前，地震加速度时程采用三角多项式逼近已经是一种常用的数值方法，借助于快速傅里叶变换方法，可快速确定三角多项式中的参数，地震作用加速度可采用三角多项式展开[21].

式中：A0为常数;Ai和Bi为三角插值公式系数;θi为谐波频率.

将式（35）代入方程（9）可得：

依据方程（36）可实现基于改进时域运动方程的傅里叶级数法，完成地震作用下结构动力响应的计算.

单自由度体系的初始状态为静止状态，利用本文提出的基于改进时域运动方程的时域计算方法（PZ1）和基于改进时域运动方程的傅里叶级数法（PZ2），计算其在地震作用下的结构加速度响应，所得结果如图2和图3所示. 其中，El Centro 波东西分量，采样周期为0.02 s，历时40 s;Taft波南北分量，采样周期为0.02 s，历时54 s.本文方法计算的加速度最大值相对误差较小（见表1和表2），证明了本文方法的正确性.El Centro 波东西分量作用下，本文方法的计算耗时为3 s，傅里叶级数法的计算耗时为110 s;Taft波南北分量作用下，本文方法的计算耗时为5 s，傅里叶级数法的计算耗时为380 s.因此，相比傅里叶级数法，本文方法的计算量更少，计算效率更高.

3   与黏性阻尼模型时域计算结果的对比分析

黏性阻尼模型存在每周期耗散能量与外激励频率相关的特点[22-23]，这与大部分材料在实验中每周期耗散能量与外频率无关的现象不一致[24]，能够更真实地描述实验现象的复阻尼模型具有每周期耗散能量与外激励频率无关的优点，但其自由振动运动方程的通解中存在发散项，造成复阻尼模型时程迭代计算结果不收敛.复阻尼模型的改进时域运动方程保留了每周期耗散能量与外激励频率无关的优点，同时保证了自由振动响应的稳定收敛.因此，基于黏性阻尼模型和复阻尼模型的阻尼力是不同的，随着阻尼比的增大，两种阻尼模型得到的阻尼力差异逐渐增大，导致动力响应的时域计算结果差异逐渐增大，当阻尼比较大时，其差异不可忽略.

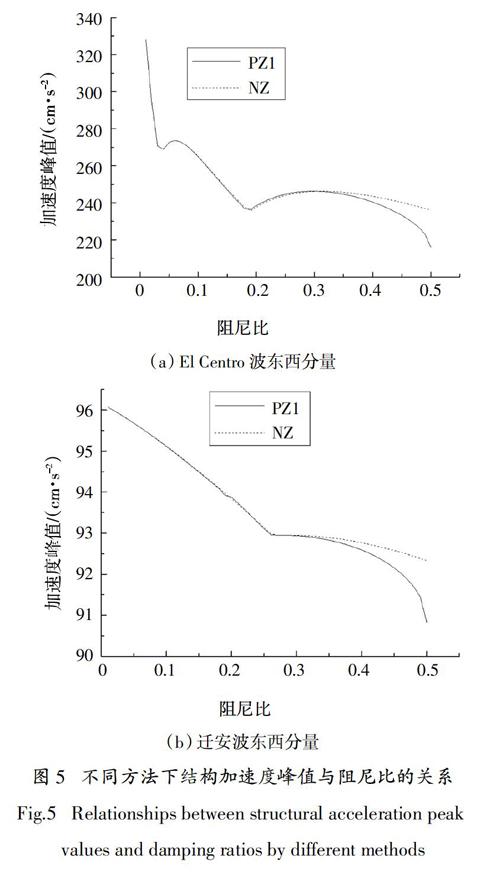
单自由度体系的初始状态为静止状态，利用本文提出的基于复阻尼模型的改进时域计算方法（PZ1）、基于复阻尼模型的高斯精细积分法（FZ）[7]和基于黏性阻尼模型的时域精确法（NZ）[19-20]，计算其在El Centro 波东西分量作用下的动力响应，所得结果如图4所示. 小阻尼情况下，随着地震作用时间的增大，PZ1、FZ和NZ的时域计算结果稳定收敛，且近似相等.当阻尼比增大时，随着地震作用时间的增加，FZ的时域计算结果出现发散现象.因此复阻尼模型的时域计算方法仅能适用于阻尼比较小和地震作用时间较短的结构体系动力响应计算分析.利用PZ1和NZ计算不同阻尼比下自振频率为4 rad/s的单自由度体系加速度峰值，计算结果如图5所示. 随着阻尼比的增大，PZ1和NZ的计算结果差别逐渐增大，与理论分析结果一致. 当阻尼比为0.5时，分别采用PZ1和NZ计算不同自振频率的单自由度体系加速度峰值，计算结果如图6所示.在El Centro波东西分量作用下，PZ1和NZ计算得到的加速度峰值相对误差最大可达到30.12%;在迁安波东西分量作用下，PZ1和NZ计算得到的加速度峰值相对误差最大可达到26.60%，差异不可忽略.

4   结   论

经过理论推导和算例分析，得出如下结论：

1）为克服复阻尼模型不能计算结构自由振动

响应的缺点，在不改变复阻尼模型的物理本质基础上，利用时频域转换原则构建了复阻尼模型的改进时域运动方程表达式，可剔除通解中发散项，进而实现自由振动响应的时域计算.

2）依据基于复阻尼模型的改进时域运动方程

特点，引入地震加速度在时间步长内是线性变化的假定，提出了相应的时域计算方法，可计算地震作用下结构的动力响应，且计算结果穩定收敛.同时，相比基于改进时域运动方程的傅里叶级数法，本文提出的时域计算方法计算量更少，计算效率更高.

3）小阻尼情况下，基于复阻尼模型的改进时域计算方法和基于黏性阻尼模型的时域计算方法得到的结果近似相等，随着阻尼比的增大，两种方法的计算结果差异逐渐增大，当阻尼比较大时，其差异不可忽略.

参考文献

[1]    董云，楼梦麟. 基于结构基频确定Rayleigh阻尼系数的优化方法及其讨论[J]. 湖南大学学报（自然科学版），2014，41（2）：8—13.

DONG Y，LOU M L. An optimization solution for rayleigh damping coefficients based on the fundamental frequency of structure[J]. Journal of Hunan University （Natural Sciences），2014，41（2）：8—13. （In Chinese）

[2]    杨永胜，陈清军. 复杂高层结构随机地震反应中阻尼模型的影响分析[J]. 湖南大学学报（自然科学版），2014，41（6）：28—34.

YANG Y S，CHEN Q J. Influence of the damping model of complex high-rise building structure on its random seismic response [J]. Journal of Hunan University （Natural Sciences），2014，41（6）：28—34. （In Chinese）

[3]    刘庆林，傅学怡，孙占琦. 基于复阻尼假定的不同材料阻尼特性混合结构抗震分析复模态叠加法[J]. 建筑结构学报，2011，32（9）：27—33.

LIU Q L，FU X Y，SUN Z Q. A complex mode superposition method for seismic analysis of structures of multiple material damping characteristics based on complex damping assumption [J]. Journal of Building Structures，2011，32（9）：27—33. （In Chinese）

[4]    朱镜清. 结构抗震分析原理[M]. 北京：地震出版社，2002：62—67.

ZHU J Q. Seismic analysis of structures [M]. Beijing：Earthquake Press，2002：62—67. （In Chinese）

[5]    朱敏，朱镜清. 逐步积分法求解复阻尼结构运动方程的稳定性问题[J]. 地震工程与工程振动，2001，21（4）：59—62.

ZHU M，ZHU J Q. Studies on stability of step-by-step methods under complex damping conditions[J]. Earthquake Engineering and Engineering Vibration，2001，21（4）：59—62. （In Chinese）

[6]    李鹏，王元丰. 黏性阻尼与复阻尼对钢筋混凝土框架结构地震响应影响的分析[J]. 地震工程与工程振动，2007，27（3）：54—57.

LI P，WANG Y F. Analysis of seismic responses of RC frames with viscous damping or complex damping [J]. Earthquake Engineering and Engineering Vibration，2007，27（3）：54—57. （In Chinese）

[7]    潘玉华，王元丰. 复阻尼结构动力方程的高斯精细时程积分法[J]. 工程力学，2012，29（2）：16—20.

PAN Y H，WANG Y F. Gauss precise time-integration of complex damping vibration systems[J]. Engineering Mechanics，2012，29（2）：16—20. （In Chinese）

[8]    张辉东，王元丰. 复阻尼模型结构地震时程响应研究[J]. 工程力学，2010，27（1）：109—115.

ZHANG H D，WANG Y F. Study on seismic time-history response of structures with complex damping[J]. Engineering Mechanics，2010，27（1）：109—115. （In Chinese）

[9]    朱镜清，朱敏. 复阻尼地震反应谱的计算方法及其它[J]. 地震工程与工程振动，2000，20（2）：19—23.

ZHU J Q，ZHU M. Calculation of complex damping response spectra from earthquake records [J]. Earthquake Engineering and Engineering Vibration，2000，20（2）：19—23. （In Chinese）

[10]  朱敏，朱鏡清. 复阻尼地震反应谱计算的再研究[J]. 地震工程与工程振动，2001，21（2）：36—40.

ZHU M，ZHU J Q. Further studies on calculation of complex damping seismic response spectra [J]. Earthquake Engineering and Engineering Vibration，2001，21（2）：36—40. （In Chinese）

[11]  何钟怡，廖振鹏，王小华. 关于复阻尼理论的几点注记[J]. 地震工程与工程振动，2002，22（1）：1—6.

HE Z Y，LIAO Z P，WANG X H. Some notes on theory of complex damping [J]. Earthquake Engineering and Engineering Vibration，2002，22（1）：1—6. （In Chinese）

[12]  REGGIO A，ANGELIS M D. Modelling and identification of structures with rate-independent linear damping[J]. Meccanica，2015，50（3）：617—632.

[13]  周正华，廖振鹏，丁海平. 一种时域复阻尼本构方程[J]. 地震工程与工程振动，1999，19（2）：37—44.

ZHOU Z H，LIAO Z P，DING H P. A time-domain complex-damping constitutive equation[J]. Earthquake Engineering and Engineering Vibration，1999，19（2）：37—44. （In Chinese）

[14]  WANG J. Rayleigh coefficients for series infrastructure systems with multiple damping properties[J]. Journal of Vibration and Control，2015，21（6）：1234—1248.

[15]  LEE J H，KIM J. Identification of damping matrices from measured frequency response functions [J]. Journal of Sound and Vibration，2001，240（3）：545—565.

[16]  尚守平，甘宜诚，蒋林. 结构振动阻尼理论模型探究及实验分析[J]. 地震工程与工程振动，2015，35（2）：166—171.

SHANG S P，GAN Y C，JIANG L. Theoretical research and experimental analysis of structural damping [J]. Earthquake Engineering and Engineering Vibration，2015，35（2）：166—171. （In Chinese）

[17]  PAN Y H，WANG Y F. Frequency-domain analysis of exponentially damped linear systems[J]. Journal of Sound and Vibration，2013，332（7）：1754—1765.

[18]  何鐘怡. 复本构理论中的对偶原则[J]. 固体力学学报，1994，15（2）：177—180.

HE Z Y. The dual principle in theory of complex constitutive equations[J]. Acta Mechanica Solida Sinica，1994，15（2）：177—180. （In Chinese）

[19]  谢礼立，于双久. 强震观察与分析原理[M]. 北京：地震出版社，1982：222—224.

XIE L L，YU S J. Observation and analysis of strong earthquake [M]. Beijing：Seismological Press，1982：222—224. （In Chinese）

[20]  张晓志，谢礼立，于海英. 地震动反应谱的数值计算精度和相关问题[J]. 地震工程与工程振动，2004，24（6）：15—20.

ZHANG X Z，XIE L L，YU H Y. Precision problems in calculating response spectra by using numerical method [J]. Earthquake Engineering and Engineering Vibration，2004，24（6）：15—20. （In Chinese）

[21]  大崎顺彦. 地震动的谱分析入门[M].吕敏申，谢礼立译. 北京：地震出版社，2008：33—35.

OSAKI Y. Introduction to spectrum analysis of ground motion [M]. Translate by L？譈 M S，XIE L L . Beijing：Seismological Press，2008：33—35. （In Chinese）

[22]  FERIANI A，PEROTTI F. The formation of viscous damping matrices for the dynamic analysis of MDOF systems [J]. Earthquake Engineering and Structural Dynamics，1996，25（7）：689—709.

[23]  MASTRODDI F，EUGENI F，ERBA F. On the modal diagonalization of viscoelastic mechanical systems [J]. Mechanical Systems and Signal Processing，2017，96：159—175.

[24]  BERT C W. Material damping：An introductory review of mathematic measures and experimental technique[J].  Journal of Sound and Vibration，1973，29（2）：129—153.