基于簇特征的增量聚类算法*

姚琳燕， 钱雪忠， 樊 路

(江南大学 物联网技术应用教育部工程研究中心，江苏 无锡 214122)

0 引 言

随着大数据时代的来临，海量的数据存储使得传统聚类方式效率低下。Fisher D[1]在1987年提出了COBWEB算法，该算法除了增加对象之外，还涉及到集群重组。文献[2,3]中讨论了与数据库动态方面有关的增量聚类，且广泛应用于许多领域[4,5]。增量聚类不需要在主存内保留对象之间的相互距离，且算法相对于对象集合的大小和属性数量可扩展[6]。

文献[7]中的层次聚类算法——BIRCH首次提出了聚类特征(cluster feature,CF)的概念，在层次增量聚类算法中取得了较好的聚类效果。受此启发，以提高准确率和时间复杂度为目标，分析K-means算法[8]和K最近邻[9](K-nearest neighbour,KNN)的优缺点，本文提出了一种基于簇特征的增量聚类算法，并在此基础上提出簇特征概念辅以KNN思想添加增量处理部分，提出一种基于簇特征的增量算法。

1 距离测量(定义一)

采用欧氏距离计算质心到数据点的距离，从点y到点m的距离为

(1)

2 基于簇特征的增量算法

为了减少迭代时间，避免算法陷入局部最优，本文提出最大距离法选取k个中心点，簇中心为c={c1,c2,…,ck}，1≤i≤k。

2.1 最大距离法选择初始中心

1)将所有的数据放入data中，中心点集合c置空。随机在Data中选取1个点作为第1个中心点，将该点放入c中，并将该点从Data中移除。

2)计算数据集Data中的所有点与随机选取的中心点的距离，选择距离最远的点作为下一个中心点并放入c中,相应的从Data中移除该点。

3)若集合c的数量等于k，结束；否则，跳入步骤(2)。

2.2 簇特征

2.2.1 CF(定义二)

本文使用mi和Fi(q)作为簇特征，CF={mi，Fi(q)，Q}。其中，mi是簇ci的中心点，Fi(q)是簇ci中距离中心点最远的q个最远点，Q是距离中心点最远的q个最远点中距离新增数据最近的点。

增量数据会对聚类结果产生影响而不会对当前的集群产生广泛的影响。数据更新之后，有3种可能性，加入已有簇，生成一个新簇或合并两个已有簇，如图1所示。

2.2.2 距离策略(定义三)

距离策略对于有效识别输入数据点Δy的正确聚类是很重要的。 在本文提出的方法中，使用了不同的距离策略，利用平均值mi，最近邻点Q和输入数据点Δy3个点。在对数据集使用改进的K-means算法聚类之后，对于即将到来的点，根据簇特征，计算新增数据点与mi之间的欧氏距离Dim(Δy，mi)，q个最远点中距离新增数据点最近的点Q和中心点mi之间的欧氏距离DQm(Q,mi)以及新增数据点与q个最远点中距离新增数据点最近的点Q之间的欧氏距离DQi(Q，Δy)，计算D=Dim+DQm×DQi的值。

2.3 更新簇特征

将某个新增数据点添加到簇后，CF的更新对数据进一步的处理至为重要。为了更新CF，首先计算发生增量簇的平均值，并更新簇特征CF的第一个分量mi。然后，利用更新的平均值mi，对增量簇中的每个数据点计算欧氏距离ED。根据计算的距离测量对数据点进行排序，并从排序列表中选择最新的q个最远邻居点，更新CF的第二个分量Fi，在下一个新增数据点进入时重新计算q个最远邻居点中距离新增数据点最近的点Q。

2.4 最近簇的合并

由于处理增量过程是每次处理一条增量数据，为了避免在增量过程中簇的数量过多形成非最优聚类结构，本文提出的方法在处理t个增量数据之后使用合并策略，使本文方法产生合理数量的簇。用于合并的过程描述为：

1)计算每个簇的平均值及和其他簇之间的欧氏距离；

2)选择欧氏距离最小的两个簇；

3)如果距离最小的两个簇之间的距离小于某个阈值MT，则合并这两个簇；

4)重新计算合并的新簇的平均值；

5)重复步骤(1)～步骤(3)，直到没有簇可合并为止。

2.5 算法具体描述

输入：静态数据集data1，动态数据集data2，合并阈值MT，阈值NT，k，t，q

输出：聚类结果re

参数：Δy为到来的新增数据点;CF为簇特征;D为欧氏距离;Fi(q)为q为最远邻居点;Q为距离新增数据最近的最远邻居点。

1)使用最大距离法选择初始中心点

2)运行K-means(data1，K)算法

3)fori=1︰k

a.计算CF={mi，Fi(q)，Q}

4)for增量数据中的每个点Δy

b.fori=1︰k

计算距离Dim和DQm和DQi

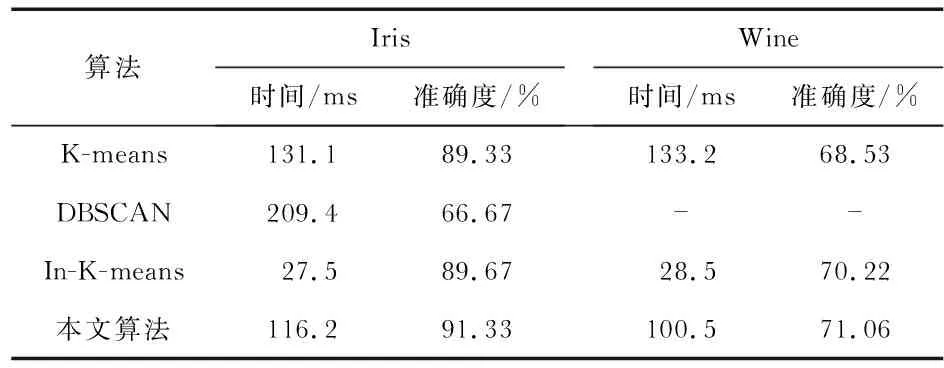
c.如果D=Dim+DQm×DQi

c1.若k个点所属簇所占比例最大的簇和i簇一致，则加入i簇

c2.若所占比例最大的簇与i簇不一致，计算所占比例最大的簇的D=Dim+DQm×DQi

若D

若大于等于NT，则加入i簇

d.如果不满足步骤(c)则生成一个新簇

e.更新簇特征CF

f.在处理完t个增量数据后

f1.计算各个簇中心点之间的欧氏距离

f2.若簇中心点之间的距离小于阈值MT则将这两个簇合并更新合并新簇的中心点，只有一个数据的簇作为噪声点返回步骤(f1)

5)得到聚类结果re

3 实验与结果分析

本文中所有的算法通过MATLAB工具实现并处理实验结果，试验环境为：CPU为Intel i3 3.7 GHz，内存为4 GB，Windows7系统。数据集：采用UCI真实数据集中的Iris数据集和Wine数据集。

实验一为了将静态数据集转化成动态问题处理，本文将数据集分为2组。鸢尾花数据集——Iris，第一组的组成为35个第一类数据，35个第二类数据，30个第三类数据。剩余数据作为增量数据作为第二组。阈值NT=10，MT=4,k=3，q=5。Wine数据第一组选取第一类簇的38个数据，第二类簇的32个数据，第三类簇的24个数据，剩下的数据作为第二组增量数据。Iris数据集阈值NT=10，Wine数据集阈值NT=10×105，t=10。

以下表格中的数据都是通过重复运行20次去掉一个最大值，一个最小值,取平均值。实验一结果如表1所示。

表1 Iris和Wine数据集实验一结果

实验结果表明，K-means算法针对Iris数据集相对DBSCAN等其他算法有比较好的聚类效果。由于IRIS数据集有两类数据有重合，所以DBSCAN不能有效识别，准确率大大低于K-means算法。由于增量数据较少，本文提出的算法较已有的增量K-means算法效率有一定的提高，但不明显。算法准确率也有较明显的提升。而增量K-means(incremental K-means,In-K-means)虽然效率较高，但准确率有所欠缺。

Wine数据中，本文所提出的算法较传统K-means算法和In-K-means算法的聚类准确率有所提高，但较Iris数据集的准确率提高程度略有降低。由于增量数据较少，效率提升也不明显。而In-K-means虽然效率较高，但准确率有所欠缺。

实验二将原始数据集中的3类样本，取其中两类作为初始聚类数据，另一类作为增量数据。为了验证本文算法对噪声点的识别能力，给Iris数据集添加人造数据10条。阈值NT=10，MT=4,k=3。噪声数据参照文献[8]，结果表明，本文算法能有效识别较远噪声点，识别噪声10条，准确度90.67 %，且算法本身较稳定，聚类算法精度较高。

4 结束语

由以上实验可以验证本文提出的基于簇特征的增量聚类算法，对于增量数据有较好的聚类精度；在处理增量数据时，避免遍历所有的数据，在一定程度上提高了算法效率，且增量数据越多，效果提升越明显。但仅能识别球形簇且时间复杂度较高，应用于大型数据集处理较为麻烦，如何结合密度，使得算法能够识别任意形状的簇或者结合网格降低算法的时间复杂度，将是下一步将要研究的工作。