基于EK-GMPHD的分布式聚类融合算法
2019-12-20胡建旺
董 青, 胡建旺, 吉 兵
(陆军工程大学 石家庄校区 信息工程系,河北 石家庄 050003)
0 引 言
当前,多目标跟踪[1]技术在空中导弹防御、跟踪与攻击、战场监视,以及医学诊断、机器视觉等方面具有十分广泛的应用。多目标跟踪方法大致分为两类:一是传统的基于数据关联的多目标跟踪算法,数据关联是这一类算法的核心,同时也是目前所面临的难点,如联合概率数据关联(joint probability data association,JPDA)[2]和多假设跟踪(multiple hypothesis tracking,MHT)[3];另一类是基于Mahler提出的有限集统计理论的多目标跟踪方法。第二类方法引入集合概念,对状态和观测进行集合处理,可以避免数据关联问题的困扰,更好地解决复杂环境中目标数目未知且随时间变化的多目标跟踪问题。对此,国内外已经开展了一系列研究,并提出了相应算法。但由于这些算法的约束条件较为严格,适应性不佳,因而没有得到广泛应用[4~6]。
此外,单个传感器对于目标进行估计时,估计结果不全面,估计精度不佳[7]。因此,在工程应用中,常使用多传感器同时工作。由于数据关联的存在,多传感器多目标跟踪算法实现比较困难,基于数据关联的分布式多传感器多目标跟踪算法实现复杂,且一旦关联错误,短时间内估计精度可能严重降低。
对此,本文提出了一种基于分布式扩展卡尔曼—高斯混合概率假设密度(extended Kalman-Gaussian mixture probability hypothesis density,EK-GMPHD的聚类融合算法。介绍了概率假设密度(PHD)滤波器与EK-GMPHD滤波算法;详细阐述EK-GMPHDF模糊C均值(fuzzy C-means,FCM)聚类融合算法,该算法跳过数据关联,在单传感器上利用EK-GMPHD滤波算法[8]对目标数目和状态进行估计,再利用FCM算法[9]进行局部航迹融合,以此形成最优全局状态估计;通过仿真实验,总结该方法的跟踪性能,进一步说明提出方法的优越性。
1 基于EK-GMPHD的分布式融合算法
基于随机有限集的PHD滤波算法将目标集当作全局目标,传感器输出的量测作为全局量测。将多目标跟踪问题放在集合定义下处理,则多目标跟踪问题转变为单目标跟踪问题,跳过了量测到航迹的关联问题,极大降低了计算复杂度。其将多目标状态模型与观测模型表示为随机有限集的形式,利用PHD函数对随机集概率密度进行近似描述,有效地解决多目标跟踪问题。
在PHD算法实现流程中,除了要满足PHD通常的假设条件外,单目标的状态转移密度和似然函数都必须是线性高斯的,若目标的运动状态模型、观测模型非线性,则需使用非线性滤波算法。因此,在中度非线性模型中,利用扩展卡尔曼对GMPHD的高斯分量进行递推,可得到较好的跟踪效果。对于系统方程
xk=f(xk-1)+wk,zk=h(xk-1)+vk
(1)
EK-GMPHD算法流程为:

2)预测:在预测阶段,新生目标密度γk(x)和衍生目标密度bk|k-1(x)可表示为
(2)
式中Jγk为新生目标密度的高斯分量数目,Jbk为衍生目标密度的高斯分量数目。因高斯混合形式是强度函数而非概率分布,故其权值之和为目标数目[10]。预测PHD函数为
Dk|k-1(x)=Ds,k|k-1(x)+Db,k|k-1(x)+γk(x)
(3)
式中Ds,k|k-1(x)为存活目标的PHD,Db,k|k-1(x)代表衍生目标的PHD,即
(4)
由于采用基于局部线性化的扩展卡尔曼算法进行分量递推,式(4)中各参量计算如下
则预测的PHD可表示为
Jk|k-1=Jb,k|k-1+Jγ,k+Jk-1
(5)
3)更新:PHD可记为
(6)
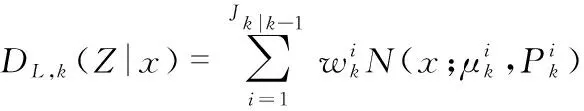


2 基于EK-GMPHDF的FCM[12~15]融合算法描述
在分布式多传感器目标跟踪系统中,将 EK-GMPHD滤波器的估计值作为xi,将模糊隶属度最大的状态预测值作为聚类中心,目标数为聚类个数。航迹融合聚类过程如下:
1)对每个传感器量测值进行EK-GMPHD滤波估计,得局部目标状态估计X1:s={X1,…,Xs},s为传感器数量。
2)用模糊聚类算法对X1:s={X1,…,Xs}进行聚类,得出模糊聚类矩阵U(k)。
3)找出U(k)的全局极值点,得到的聚类中心V(k)作为目标的状态估计,下一时刻用EK-GMPHD滤波器给出的预测值计算模糊聚类矩阵和聚类中心矩阵。
4)重复上述步骤,最终的聚类中心即为最佳估计值。
用求得的隶属度对X1:s={X1,…,Xs}进行组合,即得到全局目标状态融合估计Xf。全局目标状态融合估计为
(7)
3 仿真实验
本文提出的基于FCM的多传感器融合系统,采用分布式结构,由3只传感器组成,传感器监测区域均为[-1 000,1 000] m×[-1 000,2 500] m,杂波服从泊松分布,为便于说明问题,过程噪声与观测噪声互不相关,不考虑时间、空间对准。杂波平均数为10,采样周期为1 s,仿真时长为40 s,传感器跟踪精度分别为0.94,0.96,0.99。
图1为监控区域内目标的运动轨迹和传感器观测值,所需信息显示不明显,由3个从原点出发的运动目标组成。
图2为局部传感器经过EK-GMPHDF滤波后的跟踪结果以及神经网络(neural network,NN)算法和FCM算法跟踪目标点迹, FCM算法和3只传感器的跟踪结果与实际轨迹相较,FCM的算法估计结果更接近实际轨迹,传感器跟踪目标点迹相比偏离实际轨迹较大,这是由传感器精度决定的,NN算法估计目标位置相比FCM算法偏离较大,NN算法是局部最优算法,不能保证全局最优。

图2 局部传感器目标状态估计值和分布式融合估计值
图3为传感器和经过FCM算法后的估计目标数,传感器1,2检测概率较小,传感器估计目标数偏离实际目标数的概率较大,传感器3的检测概率为99 %,相比其他传感器,估计更为准确。因此,在其他条件不变的情况下,传感器检测概率与估计结果有关。而FCM算法估计目标数仅在4个时刻出现错误估计,优于NN算法融合结果,与实际出现目标数基本相符,充分体现了FCM算法的优越性。
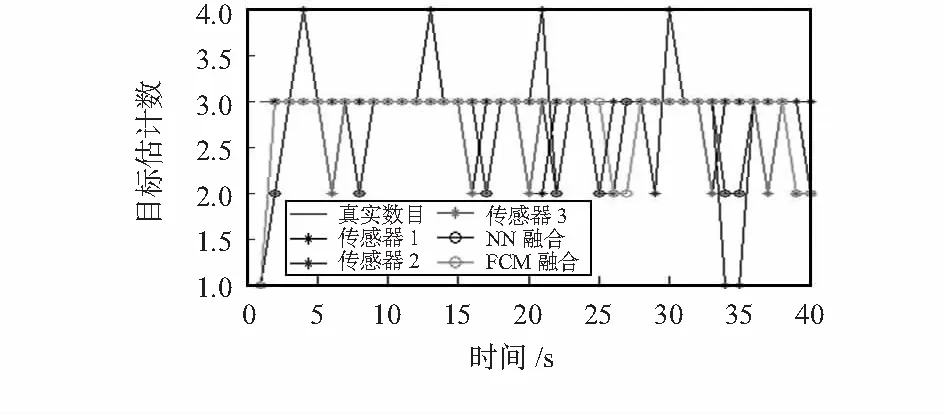
图3 目标数估计值
图4可以看出,当受到外界随机干扰时,经过FCM算法和NN算法的最优次模式分配(optimal subpattern assignment,OSPA)距离比较小,其估计精度高于其他传感器滤波结果,经过2种算法估计结果都保持较高精度,验证了2种算法具有良好的鲁棒性。从OSPA距离来看,FCM算法估计精度相比NN算法更高一些。因此,本文提出基于EK-GMPHD的FCM聚类融合算法在杂波环境中对于目标跟踪是有一定优势的。
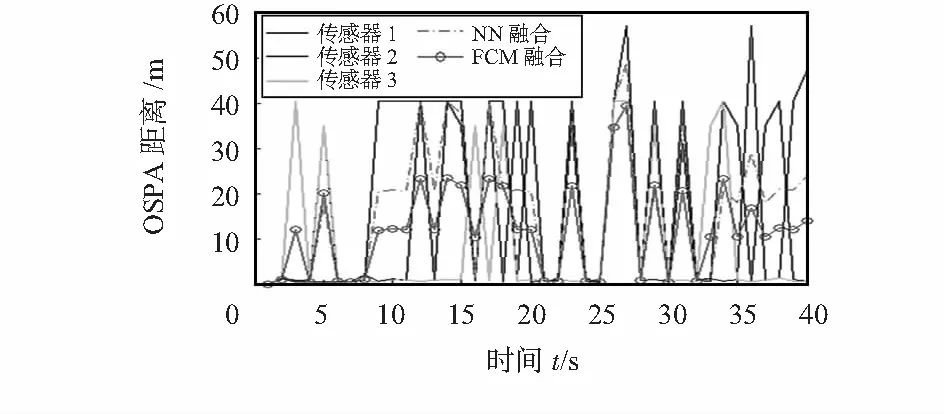
图4 局部传感器和FCM算法的OSPA距离
4 结束语
针对杂波环境中分布式多传感器目标跟踪精度低的问题,与NN算法相比,本文提出的基于EK-GMPHD的FCM聚类融合算法可更准确地估计目标状态和数目,鲁棒性增强,且计算量增加较小。仿真结果表明:本文提出的算法可提高目标跟踪精度且算法实现简单。然而随着大数据云计算技术投入使用,算法性能,鲁棒性还有待提高。下一步将基于海量数据对该算法进行研究。
