基于元胞自动机的教与学优化算法*
2019-12-20张琳琳陈俊杰倪培洲
张琳琳, 陈俊杰, 倪培洲
(东南大学 仪器科学与工程学院,江苏 南京 210096)
0 引 言
教与学优化 (teaching-learning-based optimization,TLBO) 算法是由Rao R V等人于2011年提出的一种新型群智能优化算法[1~3]。该算法基于教师对学生知识水平的影响,通过模拟教师教学和学生相互学习来实现群体的进化。相比其他智能算法,TLBO算法的优势在于算法参数极少,具有较强的并行性,且易于实现。因此,该算法已成功应用于比例—积分—微分(proportional-integral-differential,PID)控制器优化[4]、经济调度问题参数优化[5]、热电冷却器优化[6]以及飞行器气动形状优化[7]等领域,且均取得了良好的效果。
相关研究表明,TLBO算法存在易早熟、易陷入局部最优以及寻优精度低等缺点。为解决该算法的缺陷,Rao R V等人保留精英个体,用精英个体的变异个体替换种群内最差个体,提出了精英教学优化算法(elitist TLBO,ETLBO),使得算法后期收敛速度得到提高[8]。Yu K J等人[9]在ETLBO算法基础上,在学习阶段后加入反馈阶段,提出反馈精英教学优化算法(feedback ETLBO,FETLBO),在加速种群收敛的同时提高了求解精度。Chen D B等人[10]提出可变种群规模的教与学优化算法(variable-population TLBO,VPTLBO),通过种群数量的线性递增和递减来精简计算成本,提高算法收敛速度和精度。Zou F等人[11]提出了借鉴其他学习者经验的改进教与学优化算法(TLBO with learning experience of other learners,LETLBO),该算法在教学和学习阶段,新增了利用其他学习者学习经验对自身进行更新的过程,改进后的算法全局优化性能得到改善。Yu K J等人[12]针对约束优化问题提出改进教与学优化算法(improved constrained TLBO,ICTLBO),算法在教学阶段将种群分为多个子群,以加快收敛速度,同时子群间通过个体交换避免早熟。
为克服TLBO算法容易陷入局部最优的缺点,本文提出一种基于元胞自动机的教与学优化算法(cellular automaton TLBO,CATLBO)。在教学阶段提出以一定的概率接收退步个体的策略,以改善优胜劣汰导致种群多样性快速下降的缺陷;学习阶段利用元胞自动机的邻域结构,个体按照规则进行相互学习或自我学习,以提高局部搜索能力。
1 TLBO
标准的TLBO算法描述了教学过程的两个阶段:教师教学阶段和学生相互学习阶段。教师通过“教”提高种群平均水平,学生间通过相互“学”,使得劣势个体向优势个体靠近,进一步提高种群水平。种群中的每个个体都是优化问题的一个可行解。不失一般性,以最小化问题为例,问题描述如下
min(f(X))=f(x1,x2,…,xn)
(1)
X=(x1,x2,…,xn)∈S,S⊂Rn
(2)
式中S为可行解空间;n为优化问题的维数;xi∈[Li,Ui],1≤i≤n。
2 CATLBO算法
2.1 模型建立
从数学角度可将元胞自动机[13]描述为一个四元组:A=(Ld,S,N,f)。A为元胞自动机系统;Ld为元胞空间,d为空间维数;S为离散状态集;N为邻居集合;f为状态转换规则。
针对多维函数优化问题,算法在有限的迭代次数内只能搜索可行解的一个子集,即在确定的迭代次数内,种群中个体的状态可视为有限。为利用元胞自动机的局部性特征,将元胞自动机的作用机理与TLBO算法相结合建立模型,将班级的教学活动类比为一个元胞自动机演化系统,将班级视为元胞空间,采用四边形网格拓扑结构,将个体视为元胞,放置于网格中的一格,个体状态根据规则f更新。教学阶段仍然针对整个班级,个体在学习阶段根据规则f确定不同的学习方式。
2.2 教学阶段改进
原始算法采用当前最优个体指导种群进化,并采用优胜劣汰机制接收新个体,使得种群快速向最优个体周围聚集。种群多样性的快速降低,导致算法早熟,陷入局部最优解。考虑在现实教学中,教学初期由于教学次数较少,可以容忍学生成绩的退步,随着教学的反复进行,成绩退步的表现越来越不被接受。因此,为保持种群多样性,提高算法全局搜索的能力,将个体适应度的降低视为成绩的退步,以一定的概率接收适应度退步的个体,该接收概率为
(3)
种群进化初期,包容性强,当新个体出现退步时仍以一定的概率接收。随着迭代次数增加,接收概率逐渐下降至零,促使算法向全局最优收敛。
2.3 学习阶段改进
为减缓算法早熟,学习阶段不再随机选择学习对象,而是与元胞空间中的邻居个体相互学习。将学习过程限制在邻域内,减缓优秀个体影响种群的速度。为了加强算法局部搜索能力,提高解的精度,在学习阶段根据规则采用了不同的学习策略。
2.3.1 邻域结构
本文选择冯—诺依曼型个体邻域[15],即每个元胞都有上、下、左、右4个邻居。
2.3.2 个体更新规则
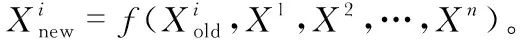
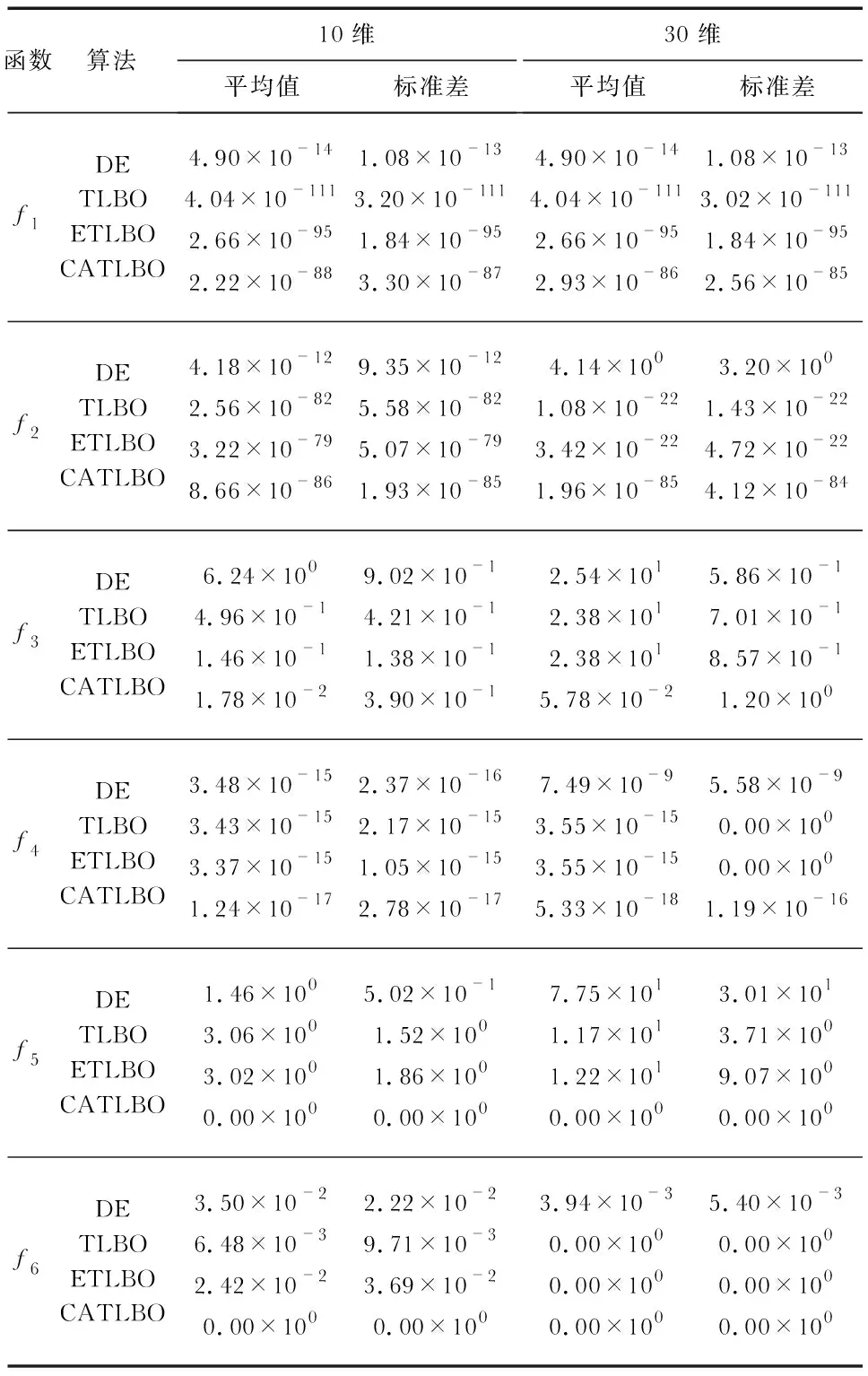
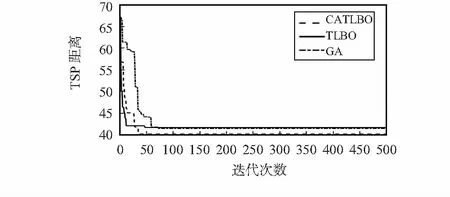
1)若满足∀Xj∈N,f(Xj) (4) 式中Xbest_nei为邻域中适应度最好的个体,即当所有邻居都比中心元胞优秀时,中心个体向邻居中的最优个体学习。 2)若满足∀Xj∈N,f(Xj)>f(Xi),则进行个体更新 (5) 即当所有邻居都劣于中心元胞时,中心元胞利用自学习算子g进行自我学习提升,以提高算法的局部勘探能力。 本文采用文献[16]中提出的分段Logistic映射,该映射比基本Logistic映射具有更好的遍历性。通过分段Logistic 映射对个体中的某两维决策变量进行扰动,产生新个体。对第i维的扰动按式(6)~式(8)执行,其中,(li,ui)为第i维变量的取值范围 (6) (7) (8) 3)若满足fmin≤f(Xi)≤fmax,进行个体更新 (9) (10) 1)设置算法参数并初始化种群。算法参数包括种群规模NP、最大迭代次数Tmax、优化问题维数D以及决策变量取值范围;根据初始化参数按高斯分布规律生成NP个随机个体。 2)以目标函数值为适应度,对种群进行评价,选出教师个体Xtea。 3) 进行教师教学阶段个体更新,对于产生的进步个体,直接接收;针对退步个体,生成(0,1)范围均匀分布的随机数R,根据适应度和当前代数按式(3)计算接收概率Pacc_new:若R 4)学习阶段,学生按照学习规则,采取不同的学习方式;若满足条件(1),根据式(4)以最优邻居个体为学习对象相互学习;若满足条件(2),则以式(6)~式(8)进行自我学习;若满足条件(3),按式(10)计算每个邻居被选中的概率Psort_j,通过赌轮选择选出邻居,根据式(9)与选中的邻居相互学习。 5)判断算法是否满足终止条件,即是否已达最大迭代次数Tmax:若否,则转向步骤(2);若是,已达到,则输出最优解。 6)输出最优解。 为了验证算法的有效性,选取文献[10]中具有代表性的6个无约束测试函数,在这6个测试函数中,f1,f2和f3为单峰值函数,其极值只有一个,解的精度在一定程度上可以反映算法的局部勘探能力;f4,f5,f6为多峰函数,在取值范围内存在大量局部极值点,可用于检验算法跳出局部最优的能力和全局收敛能力。 算法中种群规模设置为50,最大迭代次数设为500,最大函数评价次数50 000,算法终止条件为达到最大迭代次数。算法独立运行30次,以平均值和标准差作为评价指标。对于最小化问题,平均值越小越接近全局最优,表明算法寻优性能更好;标准差反映数据的离散程度,标准差越小则算法越稳定。为测试算法在处理低维和高维优化问题中的寻优效果,分别将待优化函数设置为10维和30维,测试结果列于表1。同时选取文献[10]中差分进化 (differential evolution,DE) 算法、基本(TLBO) 算法和 ETLBO 算法在相同条件下的仿真结果作为对比。 表1 10维和30维测试函数寻优结果 表1的结果表明,无论是处理单峰值还是多峰值问题、低维还是高维问题,CATLBO算法的寻优性能都明显优于DE算法。在处理单峰值优化问题上,CATLBO算法在低维和高维上表现出的优势并不明显。其中f1函数优化结果精度略低TLBO和ETLBO算法,稳定性稍差。f2,f3的求解精度略高于其他算法,稳定性与其他算法相当。 在处理多峰值优化问题时,对于f5和f6,CATLBO算法都能准确找到全局最优值,寻优性能明显优于其他算法,同时方差为零,表明算法在处理该函数时稳定。在处理另一个多峰值函数f4时,10维和30维上的实验所得平均值约为TLBO算法、ETLBO算法的1 %和0.1 %,虽未能到达全局最优,但是其寻优精度更高,更接近全局最优。TLBO算法和ETLBO算法在处理30维f4时,解的精度相对于10维时并未提高,虽然方差为零,算法稳定,但每次都陷入局部最优,显然寻优性能不如CATLBO算法。f4,f5,f6三个函数具有多个峰值,难于优化,很容易陷入局部最优,但CATLBO算法能够跳出局部最优,求解结果在均值和标准差两个指标上表现均比较优秀。因此,综合来看,CATLBO算法全局收敛性比其他算法强,能够在高维多峰值优化问题中表现出突出的优势。 在实际工程应用中,更多的是带有约束条件的优化问题,因此,选取文献[17]中的5个带约束函数进行测试。ETLBO算法中精英个数取4。种群规模取50,最大迭代次数取500,每种算法独立运行30次,以最优值、平均值和标准差作为评价指标,测试结果列于表2。同时选取文献[8]中基本TLBO算法和ETLBO算法在相同条件下的仿真结果作为对比。 表2 约束测试结果 可以看出,对于f7和f9,CATLBO算法都能稳定地收敛到全局最优解,对于f8,TLBO算法和ETLBO算法均未能找到最优解,CATLBO算法求解精度和稳定性与二者差距不大,但能够搜索到全局最优解,表明其全局搜索能力更强。在处理f10和f11上,CATLBO均能逼近全局最优解,求解精度介于TLBO算法和ETLBO算法之间。综上,在处理带约束优化问题上,CATLBO算法求解精度比基本TLBO算法有较大的提升,全局搜索能力比其他算法更具优势。 在实际工程优化中,除了上述函数优化问题,还有很多离散变量的组合优化问题。因此,为了验证CATLBO算法在组合优化中的应用效果,本文在包含13个城市的旅行商问题(TSP)[18]上对算法进行测试。除使用标准TLBO算法作为参考算法之外,还选择了遗传算法(genetic algorithm,GA),因为GA是解决组合优化的经典方法。由于TLBO算法针对的是连续函数优化,因此在解决组合优化问题时需做适当调整,算法采用自然数编码,将个体更新公式中的加减操作改为遗传算法中的交叉算子,自学习算子改为交换两个城市的位置。为了消除初始种群对算法的影响,测试时使用同一组初始种群,测试结果如图1所示。 图1 TSP收敛曲线 可知,收敛最快的是标准TLBO算法,但很快陷入局部最优。收敛最慢的是GA,但解的精度比基本TLBO算法略高,从曲线的波动可以看出GA波动较大,说明搜索范围比基本TLBO算法更广。CATLBO算法得到的解最接近全局最优,收敛速度介于二者之间。从曲线中的一段平坦区域可以看出,算法在陷入局部最优若干代后仍然能够跳出局部最优,向全局最优收敛,表明该算法全局搜索能力较强,在处理组合优化问题中也表现出一定的优势。 本文针对TLBO算法易陷入局部最优的缺陷,提出一种CATLBO算法。仿真实验的结果验证了CATLBO算法的有效性,该算法的寻优性能较基本TLBO算法有较大提高,比ETLBO等算法具有更强的全局搜索能力,适合求解高维多峰值优化问题。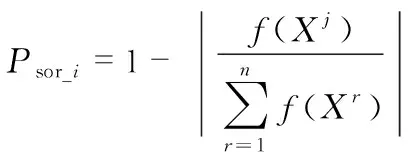
2.4 CATLBO算法流程
3 仿真测试与分析
3.1 无约束优化测试
3.2 带约束优化测试

3.3 组合优化测试
4 结 论
