粗糙集属性约简的极限学习机网络入侵检测算法*

2019-12-20周棒棒魏书宁马天雨陈远毅

传感器与微系统 2019年1期

周棒棒, 魏书宁, 唐勇, 马天雨, 陈远毅

(1.湖南师范大学物理与信息科学学院物联网技术及应用重点实验室,湖南长沙 410006；2.国防科学技术大学计算机学院,湖南长沙 410073)

0 引言

随着网络的日益扩大和开放,人们在享受网络带来便捷的同时,也受到了其带来的危害,传统的网络防护技术已经很难保障网络安全。入侵检测作为主动防护策略日益受到国内外学者的重视,如何提高网络系统的安全成了网络入侵检测系统的重要技术,对互联网和经济的持续发展具有重要意义。

刘宏立等人[1]提出了一种基于完全正弦映射混沌粒子群优化(complete sinusoidal mapping for chaotic particle swarm optimization,CS-CPSO)算法与支持向量机(support vector machine,SVM)融合的无线传感器网络(wireless sensor networks,WSNs)入侵检测算法，即CS-CPSO-SVM算法，用于提高基本粒子群优化(particle swarm optimization,PSO)算法与SVM融合的WSNs入侵检测算法的检测精度与收敛速度；王文莉等人[2]针对入侵检测系统存在的高漏报率和误报率,提出了一种基于邻域粗糙集的入侵检测方法；井小沛等人[3]提出的修正核函数的SVM算法解决了训练样本不平衡问题；沈夏炯等人[4]提出将人工蜂群优化的反向传播(back propagation,BP)神经网络模型应用于入侵检测中,避免神经网络陷入局部最优和收敛速度慢的问题；Chitrakar R等人[5]提出一种基于SVM增量算法的候选支持向量(CSV-ISVM)算法,可以使增量式学习在实际中得到较好的应用,然而由于网络数据存在冗余、数据缺失等情况的可能性较大,入侵检测系统对网络数据的训练难度仍然很大。马世欢等人[6]提出的核主成分分析—极限学习机(kernel principal component analysis,extreme learning machine,KPCA-ELM)算法,首先使用KPCA算法对数据进行降维,然后使用ELM算法建立分类器,该方法提高了小样本的学习能力,减少学习时间的同时也降低了误检率和漏检率。但KPCA特征选择方法依赖于核函数的选择,而目前也没有选择核函数及参数的指导性方法,很难选择出性能最优的核函数。

本文提出了一种基于粗糙集属性约简的ELM网络入侵检测方法,其首先利用粗糙集知识属性约简对关联和冗余属性进行约简,删除冗余和关联属性利用ELM算法对数据进行分类,有效提高了ELM的检测率。

1 网络入侵检测模型

基于粗糙集属性约简的ELM网络入侵检测模型,其基本方法是首先对提取的网络入侵数据进行离散化处理,其次使用粗糙集正域法和分辨矩阵相结合的方法对数据集进行属性约简,最后采用ELM算法建立网络入侵检测模型,具体框架如图1所示。

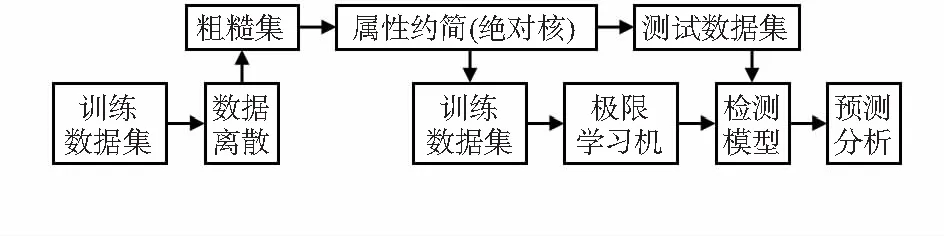
图1 粗糙集属性ELM分类方法框架

粗糙集和ELM相结合入侵检测方法的基本步骤：

1)将收集的网络数据,进行预处理,删除重复数据并使离散化;

2)对离散化的数据,先使用粗糙集的分辨矩阵方法获得分辨矩阵属性核集Core1(C),再使用粗糙集正域方法获得正域属性核集合Core2(C),最后两者结合获得绝对核Core(C)。

3)根据得到的绝对核集合Core(C),对数据进行约简,即筛选出只有绝对核属性对应的数据组成新的数据集;

4)利用ELM对新数据集生成分类模型,并使用预测数据集进行预测分类。

1.1 粗糙集网络入侵特征选择方法

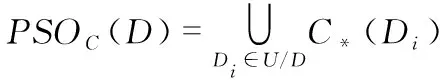
定理二在一个决策表df≤U,M∪{d},(xi,xj) ∈U×U,将βM(xi,xj)称分辨基元

βM(xi,xj)=

式中U和M为非空有限集,d为区别于M中属性的另外的属性,*为空值,a为属性,∂M为广义决策函数。

但在研究粗糙集时发现,虽然粗糙集正域和分辨矩阵方法都可以获得属性核,但两者获得属性核可能存在差异,为证明其确实存在差异使用UCI数据库中的Iris(有4个属性用A1～A4表示)、Flags(有30个属性用B1～B30表示)和简单与非(有4个属性用C1～C4表示)数据集进行展示,对比可知,数据集与非,Flags和Iris在正域的属性核分别为C1,C2,C3,C4;B1和A1,A3,A4。在分辨矩阵的属性核分别为C1,C2;B2,B5,B8,B9和A1,A2,A4。

可知通过粗糙集正域和分辨矩阵得到的属性核是可能存在不同的,由于正域和分辨矩阵都有其理论依据,因此本文提出使用集合粗糙集正域和分辨矩阵相结合方法获得绝对属性核,对数据集进行属性约简。

基本原理为假设输入网络入侵样本数为N的训练样本集合S,根据网络入侵样本集合s对样本集合进行粗糙集正域和分辨矩阵相结合方法获得绝对属性核,其步骤如下：

1)根据输入网络入侵样本集合s和设置依赖度阈值ε计算出是入侵样本集合s的条件属C相对于决策属性D集合的正域PosC(D)。

2)对于每一个ci∈C计算去掉属性ci后的相对正域Pos(C-ci)(D),如果Pos(C-ci)(D)≠PosC(D),则ci为属性核；放入Core1(C)中表示通过粗糙集正域获得的条件属性集合C的核。

3)根据输入网络入侵样本集合s,计算样本集合的分辨函数,然后对分辨函数析取范式求出样本的析取范式核Core2(C)。

4)令属性约简集合Rcd=Core1(C)∪Core2(C),计算属性约简集合Rcd依赖度kRcd(D)=|PosRcd(D)|/|U|。

5)如果kRcd≥ε,跳转到步骤(8)；否则,跳至步骤(6)。

6)对于每一个ci∈C-Rcd,计算属性重要性SIG(ci,Rcd,D)=kRcd+ci(D)-kRcd(D),存放在属性重要度集合P中,在P中选择属性重要性最大的属性Max(pi),使Rcd=Rcd∪pi。

7)计算Rcd(D)的依赖度kRcd(D)。

8)判断kRcd≥ε是否成立,若成立跳至步骤(9);否则,跳至步骤(6)。

9)输出属性约简后的属性集合Rcd。

1.2 ELM网络入侵分类器

根据属性集合Rcd对训练样本集合S进行属性约简,使样本条件属性集合xi=[x1i,x2i,…,x41i]T,i=1,2,…,N表示网络入侵数据样本原有41个属性特征,经属性核集合Rcd约简后,样本条件属性xi属性个数n<41,属性核数据集形成ELM网络入侵模型步骤如下：

1)随机设置输入层和隐含层间的连接权值w和隐含层神经元的偏值b。

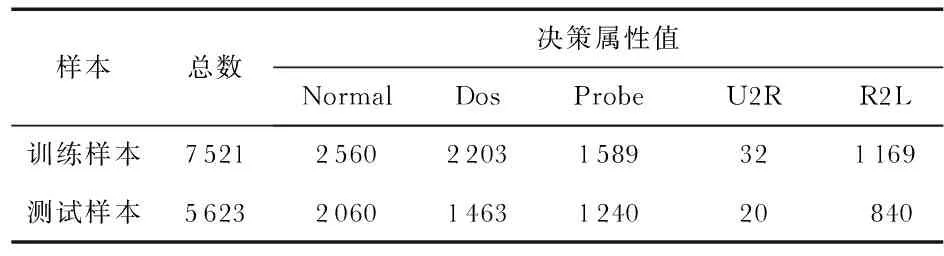
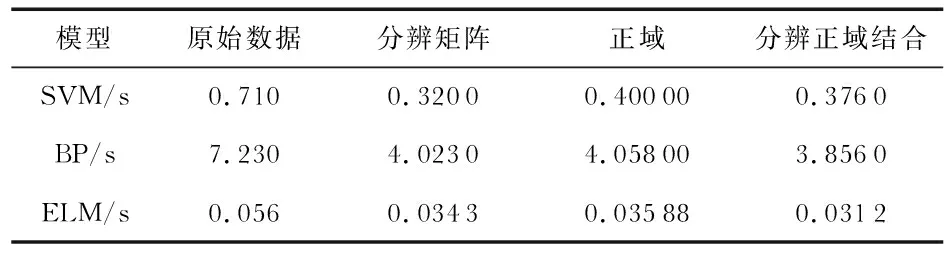
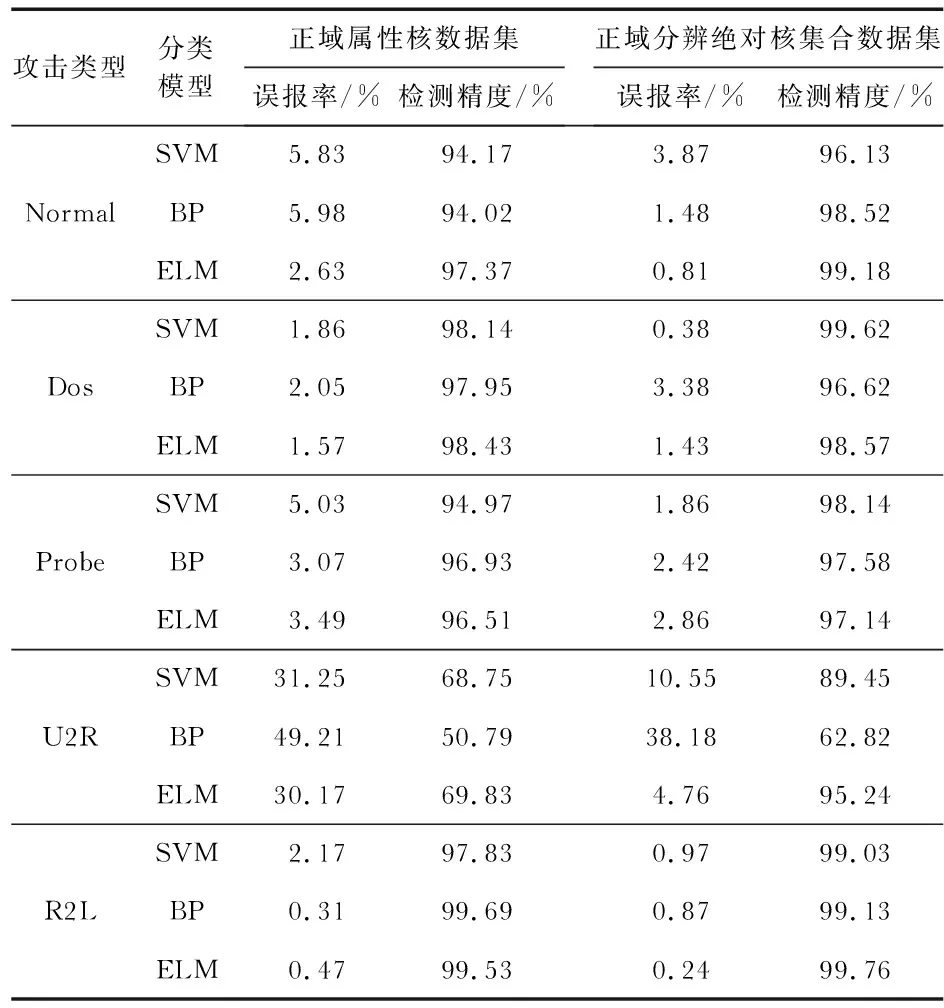
2)设激励函数为G(X)的ELM在隐含层神经元个数为L(L

Hβ=Y

(1)

式中H为隐含层的输出矩阵,可表示为

(2)

3)通过极小2—范数最小二乘解得β=H+Y,H+为H的Moore-Penrose广义逆。通过以上步骤确定隐含层和输出层权值β、隐含层和输入层权值w和偏值b,完成了ELM分类器的学习[8]。

4)输入网络入侵测试样本集合Ntest,使Rcd集合进行属性约简,然后使用式(1)获得测试样本预测值集合,从而确定模型准确率。

2 仿真分析

2.1 实验数据

实验数据集为KDDCUP99数据集,在入侵检测大赛和各种研究中应用广泛,每一个样本有42个属性值,前41个是条件属性,第42个属性是决策属性,取值有5类：Normal(正常)、Dos攻击、Probe攻击、R2L攻击、U2R攻击。

实验用A1～A41的方式表示条件属性名,用d表示决策属性。数据集如表1,在CPU为2GHz,RAM为2.00的Windows7.0系统中MATLAB 2014a上进行实验仿真。

表1 ELM在测试训练集分布

2.2 实验与结果分析

在实验中进行粗糙集的属性核,其方法为根据粗糙集分辨矩阵和粗糙集正域法相结合获得属性核(绝对核),表2为分别使用正域、分辨矩阵、两者相结合获得属性核。正域获得的核U2={A2,A3,A5,A6,A12,A13,A17,A27,A29,A30,A31};分辨矩阵获得U1={A1,A3,A4,A5,A12,A13,A24,A27,A28,A36};正域和分辨矩阵相结合的核U3={A3,A5,A12,A13,A27},但是计算其依赖度ku3小于依赖度阈值ε,可知需要在U3中加入一个除U3集合外的一个属性重要度最大的属性,然后重新计算其依赖度,直到依赖度大于ε,获得的核U={A3,A5,A12,A13,A27,A29}。再通过原始数据和绝对核集合U生成属性核对应的数据集。使用MATLAB 2014a完成SVM,BP,ELM模型的生成。根据各个属性核生成数据集在SVM,ELM,BP分类模型下训练时间如表3所示。利用原始数据生成的SVM,ELM,BP模型其预测结果分类,及利用粗糙集分辨矩阵生成的属性核由SVM,ELM,BP多种模型其预测结果分类如表4。利用粗糙集正域生成的属性核使用SVM,ELM,BP模型其预测结果分类和利用粗糙集正域和分辨矩阵结合法生成绝对属性核，由SVM,ELM,BP分类模型其预测结果分类如表5。