基于KRLS的pH中和过程建模*
2019-12-20朱瑞鹤
朱瑞鹤, 李 军
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
0 引 言
pH中和过程普遍存在于化工、污水处理等复杂工业过程中。建立反映pH中和过程系统本质特征的良好模型是进行有效控制的必要条件。早期,神经网络和模糊逻辑系统等方法已广泛应用于pH中和过程建模中[1,2],并取得了一定的应用效果;文献[3,4]采用Hammerstein及Wiener模型对pH中和过程进行辨识,文献[4]消除了辨识过程中误差累积问题,但该类模型结构表征复杂系统全局性能比较困难;文献[5]利用模糊频率响应估计法对单输出pH中和过程进行研究;文献[6,7]进一步对双输出pH中和过程进行研究。
极限学习机(extreme learning machine,ELM)是由Huang G B等人[8]提出的用于单隐层前馈网络(single-hidden layer feedforward neural network,SLFNs)的快速学习方法,文献[8]将其成功应用于非线性系统建模与控制中。支持向量机(support vector machine,SVM)等基于核学习的计算智能方法,已成功应用于化工过程建模中[9~11]。文献[9]则将核学习方法与偏最小二乘相结合,建立了丁苯橡胶聚合转化率模型,取得了较好的效果;文献[10]利用非线性偏最小二乘回归建立了pH中和过程软测量模型;文献[11]则将最小二乘支持向量机(least squares SVM,LSSVM)方法应用于双输出的pH中和过程的辨识与控制中,取得了很好的效果。同时,考虑到在线学习与时变非线性过程的特性,文献[12]给出了一种用于时变在线自适应过程的核学习方法——核递推最小二乘(kernel recursive least squares,KRLS)方法,其基于近似线性依赖(approximate linear dependency,ALD)技术限制核矩阵的大小,并成功应用于混沌时间序列预测中。鉴于LSSVM等方法在过程建模中的成功应用,针对复杂的非线性pH中和过程,本文提出基于KRLS的核学习建模方法,将其应用于典型pH酸碱中和过程实例中,以进一步提高复杂非线性化工过程的建模精度及计算效率。在同等条件下,本文方法还将与核偏最小二乘(kernel partial least square,KPLS)、核主成分分析—支持向量机(kernel principal component analysis-support vector machine,KPCA—SVM),核函数极限学习机(extreme learning machine with kernel,KELM),极限学习机(extreme learning machine,ELM),SVM,LSSVM等现有方法进行比较,以验证所提方法的有效性。
1 KRLS方法
1.1 基于ALD条件的稀疏化

为考虑是否将数据xt加入字典中,需求得满足ALD条件的系数向量a=[a1,…,amt-1]T,即有
(1)
式中 阈值参数μ的取值大小影响稀疏化程度。
考虑k(xi,xj)=φ(xi)Tφ(xj),由式(1)得到
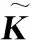
(2)

对式(2)求解,可得到最优系数向量a及ALD条件
(3)
借助ALD条件,直至t的所有数据均能由字典集合Dt中数据向量的近似线性组合来表示。由式(1)可得
(4)
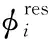
延伸至特征空间,定义矩阵

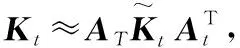
1.2 ALD-KRLS方法
针对pH中和过程输入输出数据,完成基于ALD的KRLS方法的训练,建立输入与输出之间的非线性映射关系f(x)。
t时刻,由RLS算法可知,最小化误差平方和满足
(5)

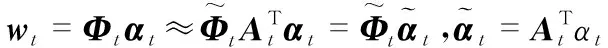
基于ALD的KRLS方法的算法具体实现步骤如下:
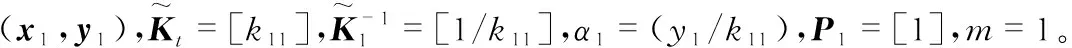
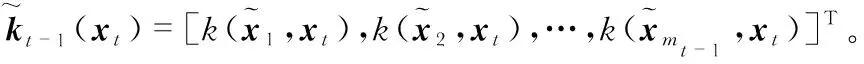
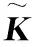
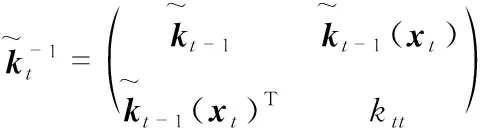
(6)
由于xt是字典中的数据向量,相应有

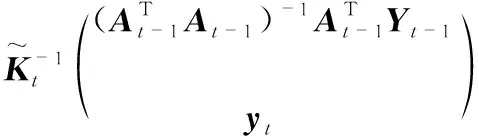
(7)

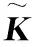
(8)
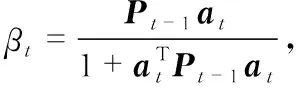
(9)

5)迭代计算步骤(2)~步骤(4),直至所有训练数据依次完成。
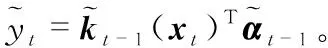
若训练数据的数目为l,则KRLS算法的计算复杂度为O(lm2)。
2 pH中和过程实验应用
pH中和过程即通过酸液流入物和碱液反应物之间的中和,检测反应过程流出物的pH值。pH值定义为溶液酸碱度,pH=-log[H+],其中H+为氢离子。实验中,需对数据进行归一化处理,并采用均方误差(mean square error,MSE)来评价模型的辨识性能。核学习方法均采用高斯径向基核函数,即有
(10)
式中 σ(σ>0)为高斯核函数的核宽度参数。
具有缓冲流的双输出酸碱中和反应过程实验装置如图1所示。
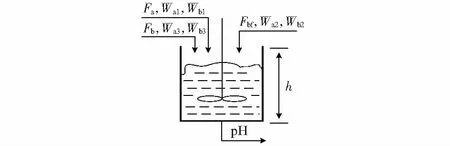
图1 双输出pH中和过程反应装置
设定过程的输入为酸液(HNO3)流量Fa,缓冲液(NaHCO3)流量Fbf,碱液(NaOH+NaHCO3)流量Fb,输出分别为流出物的pH值和CSTR的液位h,系统参数的取值同文献[1]。定义物理量符号如下
wa为电平衡常数,wb为离子平衡常数。则CSTR中的双输出pH中和过程动态模型可表示为
dx/dt=f(x)+g(x)u+p(x)d,c(x,y)=0
(11)
式中x=[x1x2x3]T,x1=h,x2=wa,x3=wb,u=[FaFb]T,d=Fbf,y=[hpH]T,c=[c1c2],且
(12)
式中A为反应釜的面积,Cv为阀门参数,Wa1~Wa3,Wb1~Wb3为反应常数。CSTR过程中,给定流入溶液流量变化为
Fa(t)=16+4sin(2πt/15)
Fb(t)=16+4cos(2πt/25)
Fbf(t)=0.55+0.055sin(2πt/10)
(13)
根据式(11)描述的机理模型,以及式(13),产生600组数据集,前300组为训练数据集,其余作为测试数据集。考虑辨识模型如下
ypH(t-1),yh(t-1)]
(14)
式中 模型ψ[·]采用KRLS方法建立。
通过交叉验证方法选取KRLS,KPLS,KPCA-SVM,KELM方法的核参数σ=0.1,KRLS最大字典容量mmax=200,阈值μ=0.01。对比实验中,KPLS的潜在变量数目L=50,KPCA-SVM方法中,选取非线性主元数目为20,SVM为线性核函数。单一SVM方法中,SVM采用台湾大学林智仁教授等开发设计的LIBSVM软件完成,惩罚因子c=200,ε=0.01,ELM方法中,隐含层节点数目为120,节点激活函数为Sigmiod函数。
表1给出了在同等条件已有文献及SVM等其他方法结果的精度对比,可以看出,在测试数据集上KRLS方法的精度均明显占优,其中KRLS的精度提高了约1个数量级。
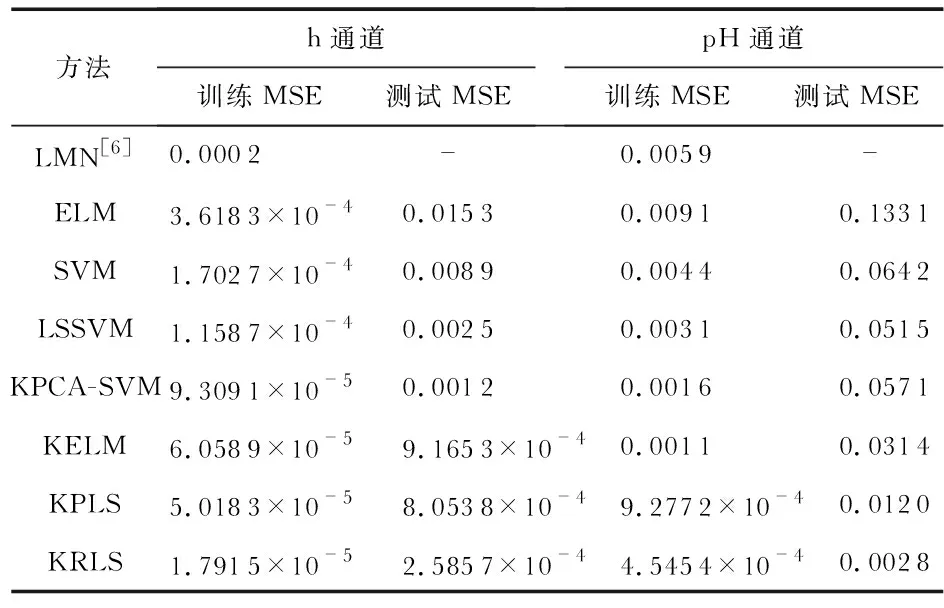
表1 KRLS模型建模性能比较
图2给出了KRLS方法在训练集上的学习收敛曲线,看出,KRLS辨识模型表现出了良好的在线自适应学习特性。图3、图4分别给出了在测试数据集上h通道和pH通道的测试输出与真实值的结果比较曲线,图5给出了在测试数据集上h通道和pH通道的各点测试误差比较曲线,从图2~图5的结果可以看出,在多输出的情形下,KRLS方法呈现出较好的建模性能,验证了该方法的有效性。
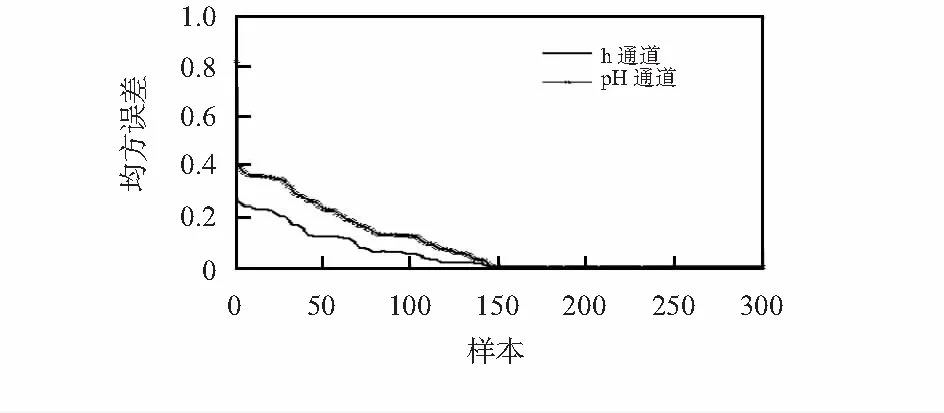
图2 KRLS模型训练误差学习曲线

图3 KRLS模型h通道上的测试输出
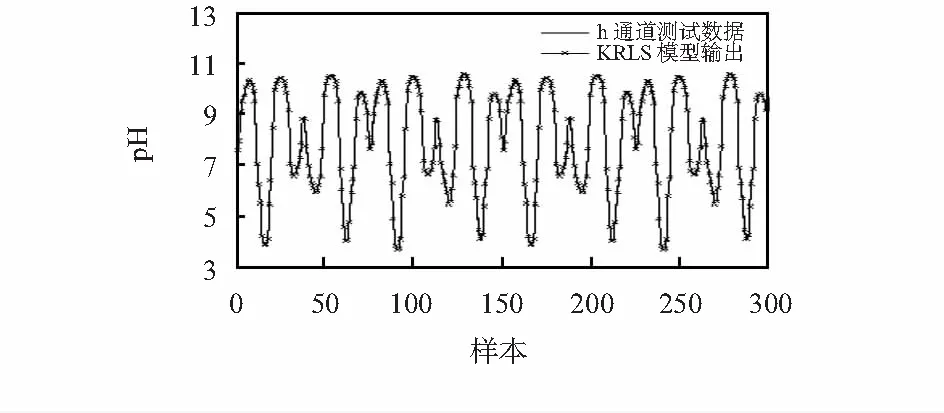
图4 KRLS模型pH通道上的测试输出

图5 KRLS模型测试误差
3 结束语
本文针对未知的复杂非线性pH中和过程,从系统输入输出数据出发,提出了基于核学习的KRLS建模方法。与ELM及其他核学习方法相比,本文方法在计算效率、建模精度等方面均呈现出良好的性能。KRLS方法适用于较大规模数据集时变非线性过程的建模,为难以得到精确数学模型的复杂工业过程建模提供了新思路。
