循环平稳算法的脉搏信号噪声评估指标

任亚莉，仵博万

(陇东学院电气工程学院，甘肃 庆阳 745000)

0 引言

近年来，循环平稳理论不断得到完善和发展，在通信、雷达等领域得到广泛的应用[1-2]。脉搏波信号是重要的人体生理信号。脉搏波特征变化是评价人体心血管系统生理状态的重要依据[3-5]。脉搏信号的每个脉动周期不完全一样，并非严格的周期信号。其属于非平稳信号，但却呈现出一定周期平稳性，即脉搏信号具有循环平稳特性[6]。与脉搏信号类似，心音信号也属于循环平稳信号[7]。有学者将循环平稳算法应用于心音信号的质量评估和包络估计，取得了一定的研究成果[8]，可作为脉搏信号噪声评估的参考。

脉搏信号在采集过程中不可避免地受到基线漂移、肌电干扰和工频干扰等噪声的影响[9-10]。这些噪声不仅会降低脉搏信号的质量，而且会淹没有用的信号,导致医疗监护设备错误报警，增加病人和医护人员的压力，造成医护人员对报警信号的不信任和麻痹大意。这严重影响了对真实危重疾病的报警和及时响应与处理。

为了获得准确的脉搏信号，以便后续分析以及病情诊断，需要采取相应方法对采集的信号进行噪声评估。这需要提取并分析噪声最小的信号段。

有关脉搏信号质量评估方面的文献不多[11-13]。本文将这些研究成果作为参考，提出了基于循环平稳算法的脉搏信号噪声评估指标——质量因数，用于评估脉搏信号受噪声影响程度。采用建模产生的仿真脉搏信号、MIT-BIH数据库提供的实际采集脉搏信号叠加噪声信号，验证所提出方法的准确性和实用性。

1 脉搏信号质量因数的提出

(1)

式中：δx(α)为循环频率频谱密度。

根据此定义，脉搏信号质量因数为：

(2)

式中：max[δx(α)]为δx(α)的峰值;η为最大循环频率;λ为基本循环频率，即δx(α)波形的峰值所对应的频率位置。

噪声和干扰会影响脉搏信号的循环平稳特性。因此，通过质量因数的大小，可评估脉搏信号受噪声影响程度。

将式(2)应用于脉搏信号，可得到一整段脉搏信号的质量因数。其为常数，不能反映脉搏信号局部噪声变化。为了能计算出一段脉搏信号各处的质量因数，引入滑窗：给脉搏信号加入一个动态的窗口，窗宽记为2δ，采用式(2)计算该窗口([t-σ,t+σ])内的信号质量因数，并将其作为t时刻的质量因数。此时，式(2)变为：

(3)

式中：δx(α,t)为在([t-σ,t+σ])窗口内脉搏信号的循环频率频谱密度。

通过式(3)可知，c(λ,t)为随时间变化的质量因数，简称时变质量因数。对于c(λ,t)而言，如果滑窗的长度太短，无法体现脉搏信号的循环平稳特性，也就无法得到循环频率α。所以滑窗宽度不能小于2个完整的脉搏周期。

2 仿真试验

2.1 试验数据

选取4组不同类型脉搏信号进行试验分析。

第1组：选取由三个高斯波合成的仿真脉搏信号[15-16]，每个高斯函数由三个参数确定，即幅度V、时间T和宽度U。合成信号表示为：

(4)

式中：V1=0.8,V2=0.5,V3=0.4;T1=0.25,T2=0.45,T3=0.7;U1=0.012,U2=0.01,U3=0.03。

三个高斯波合成的仿真脉搏信号波形如图1所示。

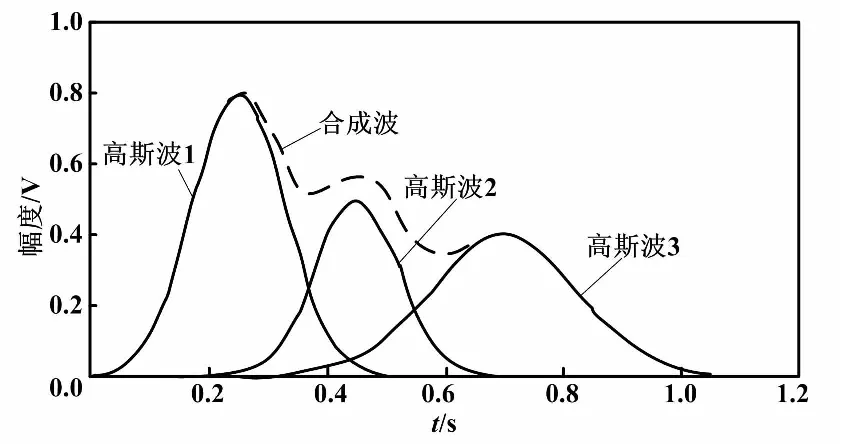
图1 三个高斯波合成的仿真脉搏信号波形图

对式(4)的单个脉搏信号进行延拓，产生一组脉搏信号x(t)，并将其作为干净脉搏信号。1 s的信号含有250个数据点，信号总长度为10 s。为了消除信号幅值不同的影响，将其归一化，均值为0，标准差为1。归一化公式如下：

(5)

式中：mean[x(t)]、std[x(t)]分别为原始脉搏信号x(t)的均值和标准差；s(t)为归一化后的脉搏信号。

归一化后的仿真脉搏信号波形如图2所示。

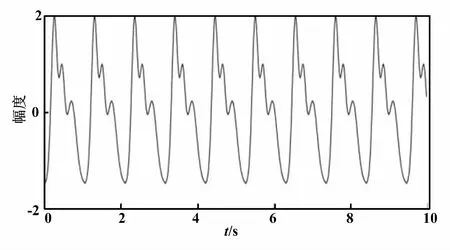
图2 仿真脉搏信号波形图

第2组：选取MIT-BIH/Physio Net /Fantasia 数据库中10位年轻人数据(21～34岁，名称为f2y01m～f2y10m)，采样频率为250 Hz。

第3组：选取 MIT-BIH/Physio Net/Fantasia 数据库中10位老年人数据 (68～85岁，名称为f2o01m～f2o10m)，采样频率为250 Hz。

第4组：选用 MIT-BIH/Physio Net /MGH_MF数据库中11位心律不齐病人数据(名称为a40006_000025 m，a40006_000000 m、02 m、05 m、07 m、08 m、10 m、12 m、21 m、22 m、23 m、25 m)，采样频率为125 Hz。

数据库提供的噪声信号有基线漂移和肌电干扰。基线漂移数据名称为bwm，肌电干扰数据名称为mam。信号采样频率250 Hz。

记噪声信号为10 s，则n(k)=a×mam(k)+b×bwm(k)，其中：a、b为噪声系数，可调节噪声大小。

2.2 质量因数的计算

选取长度均为10 s的4种信号：仿真脉搏信号(信1)、f2y06m(信2)、f2o03m(信3)、a40002_000005m(信4)。按式(5)进行归一化处理；再截取10 s噪声信号n(k)，分别加入4种信号作为分析信号。调整a、b大小，得到共15组数据，并通过式(6)计算信噪比(signal-to-noise rate,SNR)：

(6)

式中：sts为信号方差;stn为噪声方差[17]。

信噪比与噪声系数关系如表1所示。

表1 信噪比与噪声系数关系

图3 仿真脉搏信号循环谱估计图

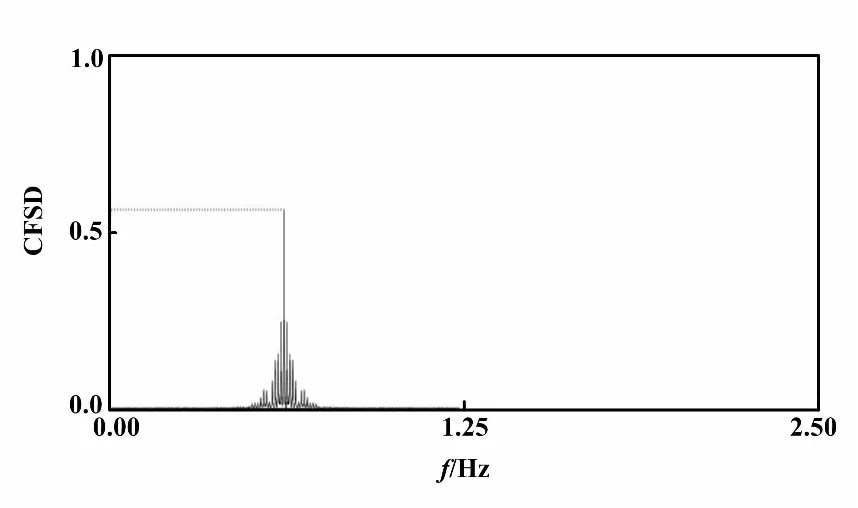
图4 心律不齐脉搏信号循环谱估计图

通过试验可知，基本循环频率λ、最大循环频率η及积分大小只与信号数据点多少有关，与噪声等其他因素无关。图3信号数据点为2 500，图4信号数据点为1 250。所以两种信号上述三种量的值不同。

对前述的10 s 的4种信号(信1、2、3、4)，在15组信噪比的情况下通过SSCA估计循环频谱密度，其循环频谱密度峰值与信噪比关系如图5所示。由图5可知，信噪比越大，CFSD峰值越小。

根据式(2)计算质量因数，质量因数与信噪比关系如图6所示。由图6可知，信噪比越大，质量因数越大，质量因数可以很好地评估脉搏信号噪声情况。在相同信噪比情况下，正常脉搏信号质量因数远大于心律不齐信号质量因数。这主要是因为式(2)分子积分值差别大，正常脉搏信号为3.12,心律不齐信号为0.78。

图6 质量因数与信噪比关系图

2.3 时变质量因数的计算

2.3.1 仿真脉搏信号

选取30s仿真脉搏信号，每10 s为一段，加入大小不同的噪声信号n(k)，采用式(3)计算时变质量因数。滑窗宽8 s，步长1 s，计算23段信号质量因数，分别对应4～26时刻，间隔1 s。当三段信噪比较小，分别为SNR1=1.52 dB、SNR2=0.46 dB、SNR3=1.01 dB时，仿真脉搏信号曲线如图7所示。

图7(a)中，1～9s数据信噪比最大，为SNR1=1.52 dB。从图7(b)可以看出，质量因数随时间变化情况完全反映了信号噪声大小；5 s时质量因数达最大值2.32(A点所示)，此时窗口对应1～9 s数据，该段信号噪声小。

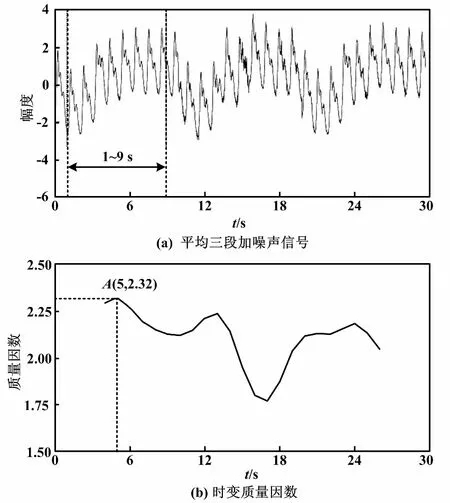
图7 仿真脉搏信号曲线

通过改变步长，反复试验结果表明，质量因数评估信号受噪声影响程度的准确性主要取决于各段信号信噪比差别大小，差别越大，越准确；其滑窗宽度及步长的选取没有多大关系。此结论对下面实际采集的脉搏信号也适用。

2.3.2 年轻人脉搏信号

选取10组年轻人脉搏信号30 s，每10 s为一段，加入大小不同的噪声信号n(k)，采用式(3)计算时变质量因数。滑窗宽8 s，步长2 s，计算12段信号质量因数，分别对应4～26 s时刻，间隔2 s。

当10组信号三段信噪比平均约为SNR1=5.39 dB、SNR2=16.73 dB、SNR3=1.24 dB时，f2y02m～f2y10m共9组数据质量因数最大时对应10～18 s或12～20 s数据段。该两段数据信噪比最大，只有f2y01m信号质量因数最大时对应8～16 s数据，但靠近信噪比大的数据段。

对于f2y10m数据，当三段信噪比为SNR1=5.97 dB、SNR2=9.76 dB、SNR3=8.42 dB时，年轻人脉搏信号时变质量因数如图8所示。图8(a)中，12～20 s数据信噪比最大，为SNR3=8.42 dB。从图8(b)可以看出，质量因数随时间变化情况完全反映了信号噪声大小，16 s时质量因数达最大值3.96(A点所示)，此时窗口对应12～20 s数据，该段信号噪声小。

图8 年轻人脉搏信号曲线

2.3.3 老年人脉搏信号

选取10组老年人脉搏信号，时长30 s，前后10 s两段加入大小不同的噪声信号n(k)，采用式(3)计算时变质量因数。滑窗宽8 s，步长1 s，计算23段信号质量因数，分别对应4～26 s时刻，间隔1 s。

对于f2o03m数据，当两段信噪比为SNR1=2.69 dB、SNR2=0.72 dB时，试验结果如图9所示。

图9 老年人脉搏信号时变质量因数

当10组信号两段信噪比平均约为SNR1=2.46 dB、SNR2=0.73 dB时，10组数据质量因数最大时对应10～18 s或12～20 s数据段，该两段信号无噪声。

从图9(a)可以看出，质量因数随时间变化的情况完全反映了信号噪声大小。14 s时，质量因数最大值达4.3。此时窗口对应10～18 s数据，如图9(b)所示，该段信号无噪声。

2.3.4 心律不齐脉搏信号

选取10组心律不齐脉搏信号(a40006_000000 m，02 m，05 m，07 m，08 m，10 m，12 m，21 m，22 m，23 m，25 m)，时长30 s。前15 s段加入大小不同的噪声信号n(k)，采用式(3)计算时变质量因数。滑窗宽10 s，步长1 s，计算21段信号质量因数，分别对应5～25 s时刻，间隔1 s。

当10组信号前段信噪比平均约为SNR=3.96 dB时，10组数据质量因数最大时对应后15 s数据段。该段信号无噪声。

对于a40006_000025m数据，当前段信噪比为SNR=4.51dB时，心律不齐脉搏信号曲线如图10所示。从图10(a)可以看出，质量因数随时间变化情况完全反映了信号噪声大小，21 s时质量因数达最大值1.54。此时窗口对应16～26 s数据，如图10(b)所示，该段信号无噪声。

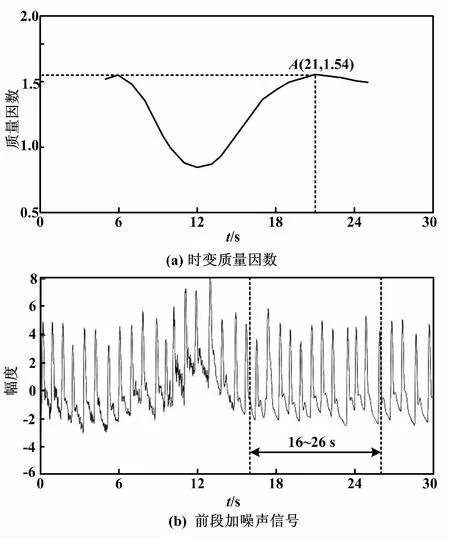
图10 心律不齐脉搏信号曲线

3 结束语

本文提出的基于循环平稳算法的质量因数，能够比较准确地评估脉搏信号受噪声影响程度。大量仿真试验结果表明，质量因数越大，则受噪声影响越小；质量因数越小，受噪声影响越大。使用质量因数，计算机就可以自动分辨出哪一段脉搏信号的噪声小，所以只需分析这一段信号，以节省消除噪声等预处理的过程、减少计算量和处理时间。

通过大量试验发现，信号各段信噪比差别越大，准确率越高，信噪比越接近(不同脉搏信号情况不一样)；时变质量因数最大时对应的不一定是噪声最小数据段，但基本靠近噪声小数据段，所以该方法的准确性有待提高。

综上所述，质量因数可以判断脉搏信号受噪声污染程度，并且能够利用它在一整段脉搏信号寻找出没有噪声或噪声小的一段，以方便后续对信号作进一步分析处理。