改进禁忌-神经网络在小电流接地系统选线中的应用
2019-12-20覃禹铭任庭昊胡兵轩代启璨
覃禹铭,任庭昊,胡兵轩,代启璨,车 洵
(1.贵州电网有限责任公司遵义供电局,贵州 遵义 563000;2.南京南瑞继保电气有限公司,江苏 南京 210000)
0 引言
我国10~35 kV电网大多采用小电流接地方式,地处南方雷雨潮湿环境,发生单相接地故障的概率很高,并有可能弧光接地发展为两相短路。因此,迫切需要一种自动快速确定故障线路的方法,以保障电网稳定运行[1]。
不同故障条件下的有效故障特征分量差异较大。这是影响选线准确度的主要因素[2-4]。目前,选线方法有稳态法和暂态法。稳态故障分量一般较小,难以检测[5-6]。暂态法的优点是故障特征分量明显,但若采用单一判据,故障分量的差异会造成误判[7-10]。为此,融合多种判据的选线策略得到了广泛应用[11-14],其中大多采用反向传播(back propagation,BP)网络。
相较于BP网络,径向基(radial basis fuction,RBF)网络的学习效率和逼近精度更高[15-16]。本文将RBF网络应用于小电流接地选线,采用禁忌算法训练RBF网络,仿真验证该方法的泛化性能和选线精度。
1 RBF网络模型
本文采用单隐层前馈的三层RBF神经网络结构,隐单元的激励函数选用RBF函数。这里取高斯核函数。作为一种局部逼近神经网络,隐单元输出的线性加权和构成网络输出。RBF网络模型如图1所示。
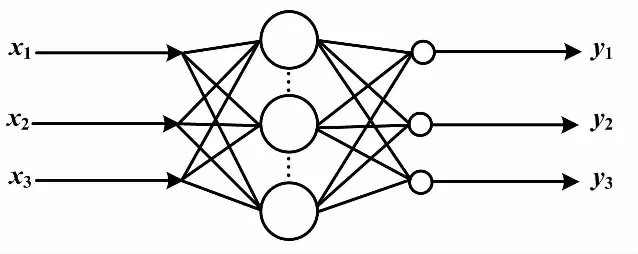
图1 RBF网络模型
网络结构参数对于RBF网络非线性逼近能力至关重要。网络结构如果过于简单,网络对样本的学习能力不够;反之则容易导致过度拟合,降低神经网络的泛化能力。特别在面对小电流接地系统复杂多变的故障状况时,容易出现选线误判的情况。因此,对RBF网络结构参数的优化尤为必要。RBF网络结构参数较多,但最关键的是隐含层与输出层之间的连接权值,以及隐含层的中心和宽度。
2 禁忌算法优化RBF网络
2.1 禁忌算法主要思想
容易陷入局部最优是BP神经网络的主要缺陷。为了避免这一点,禁忌搜索(tabu search,TS)法模拟人脑智能,允许搜索方向背离目标函数,从而扩大了搜索范围。但该方法同时带来盲目搜索的问题。为此,引入禁忌表,其中保存了搜索历史过程中移动的逆方向。这些移动在新的搜索中是被禁止的,从而回避无效搜索。禁忌表使得TS算法有效地跨越了局部最优的陷阱,但也可能误将某些指向更优解的移动禁止。为了弥补这一点,又引入“藐视准则”,规定当某个移动可能寻找到更优解或该移动在禁忌表中的保存任期(禁忌长度)已到,则从禁忌表中释放该移动。TS法的随机搜索通过禁忌表的“禁止”和“藐视准则”的释放,达到算法收敛性和种群多样性之间的微妙平衡,其目的在于提高搜索效率的同时不错过最优解。
2.2 关键参数及其改进
TS算法最重要的三个参数为邻域范围、禁忌条件和终止条件,分别对应搜索起始、中间和结束三个阶段。
TS算法从初始解的邻域开始搜索。邻域范围设置得大,搜索范围广,但搜索效率会降低;反之,邻域设置过小,则无法保证搜索多样性。因此,本文在优化的不同阶段选取不同邻域:起始阶段应强调搜索多样性,邻域设置得大一些;最后阶段搜索最优解、减小邻域范围、加强搜索强度,以便快速找到最优解。
搜索过程中,为了跳出局部极小的陷阱,禁忌表中禁止发生过的历史移动。但一般均以移动的步长作为禁止条件。问题是,这一条件范围太大。那些尚未访问过的状态点如果步长落入该范围,也会被禁止,有可能错过指向最优解的移动。为此,本文将禁止条件改为访问过的状态点及其步长,使禁忌范围更精确地指向无效搜索。
逼近最优解的阶段,迭代终止条件的确定将影响到优化时间和解的精度。如果以迭代数作为终止条件,虽然优化时间可以确定,但解的精度无法保证。如果以允许误差为终止条件,可以满足收敛精度,但优化时间可能较长;况且在最优解还未找到前,允许误差仅是估计值。为了平衡优化时间和解的精度,本文采用迭代周期的办法,在每个迭代周期中以本周期最优解和上周期最优解的优劣作为是否继续迭代的判据。
2.3 改进禁忌算法训练RBF网络的步骤
禁忌算法寻优的主要过程可描述为:任选一初始解,从初始解的邻域中随机产生一系列新状态,计算所有状态的目标函数,找到对应最优目标函数的状态,取为当前最优状态;继续迭代,一直持续到满足设定的终止条件为止。其具体步骤如下。
①在定义域N(X)任选初始解X,设所有移动的状态点及其步长集合为B、禁忌表状态点及其步长集合为J、迭代数设为N、初始化J=0、N=0,目标函数为f。
②对不在禁忌表J内的状态点及其所有步长Bj∈B-J,从初始解X的邻域随机产生一个新状态Z。
③计算X和Z的目标函数f(X)和f(Z)。若f(Z)>f(X),放弃新状态Z,迭代数N=N+1,转步骤②重新产生新状态。
若对所有的新状态Zi满足f(Zi)>f(X),并且满足终止条件,算法终止。
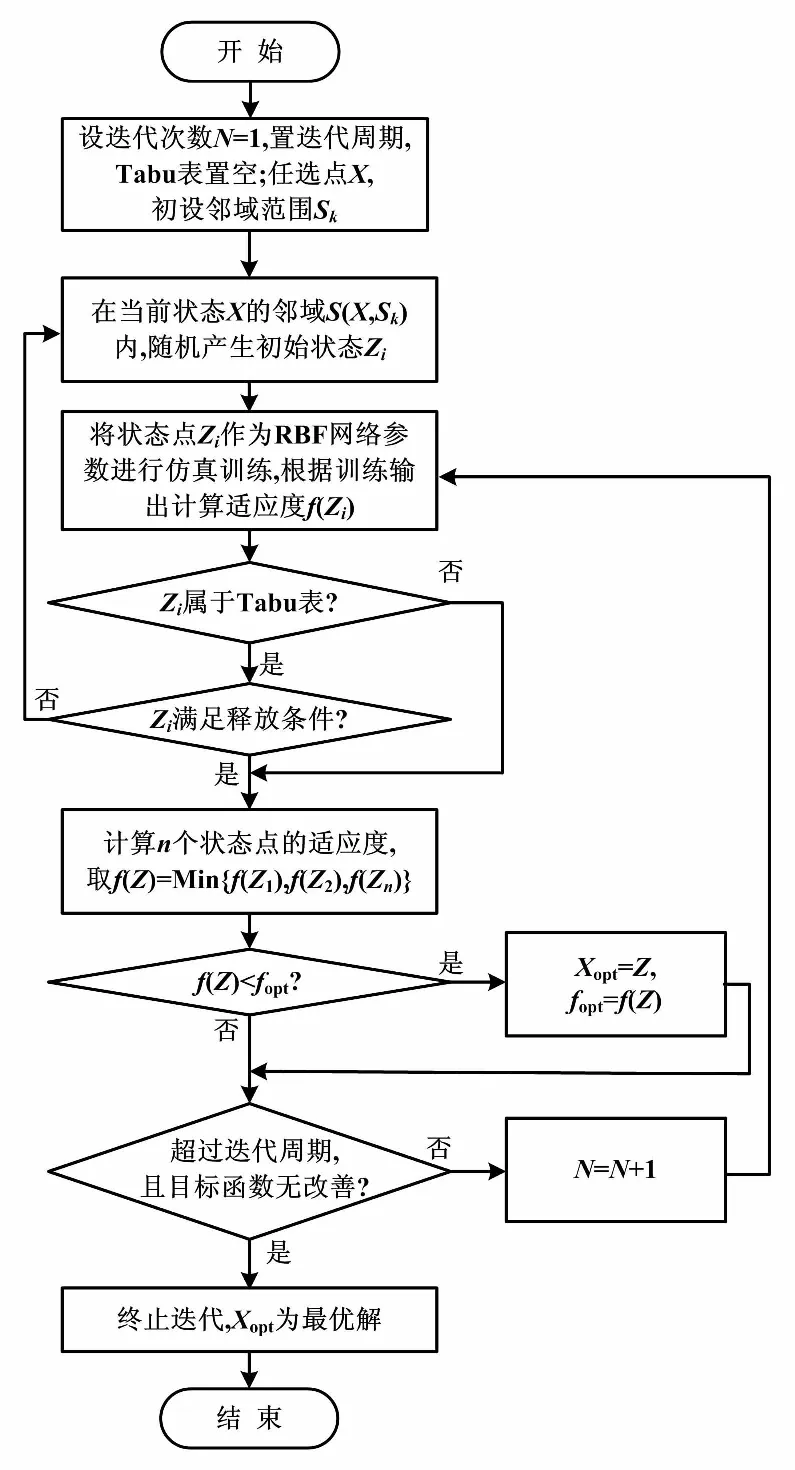
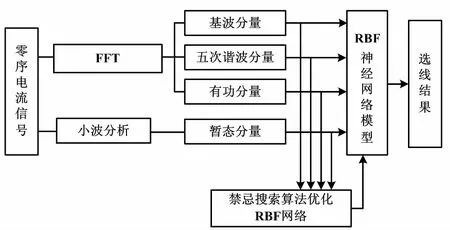
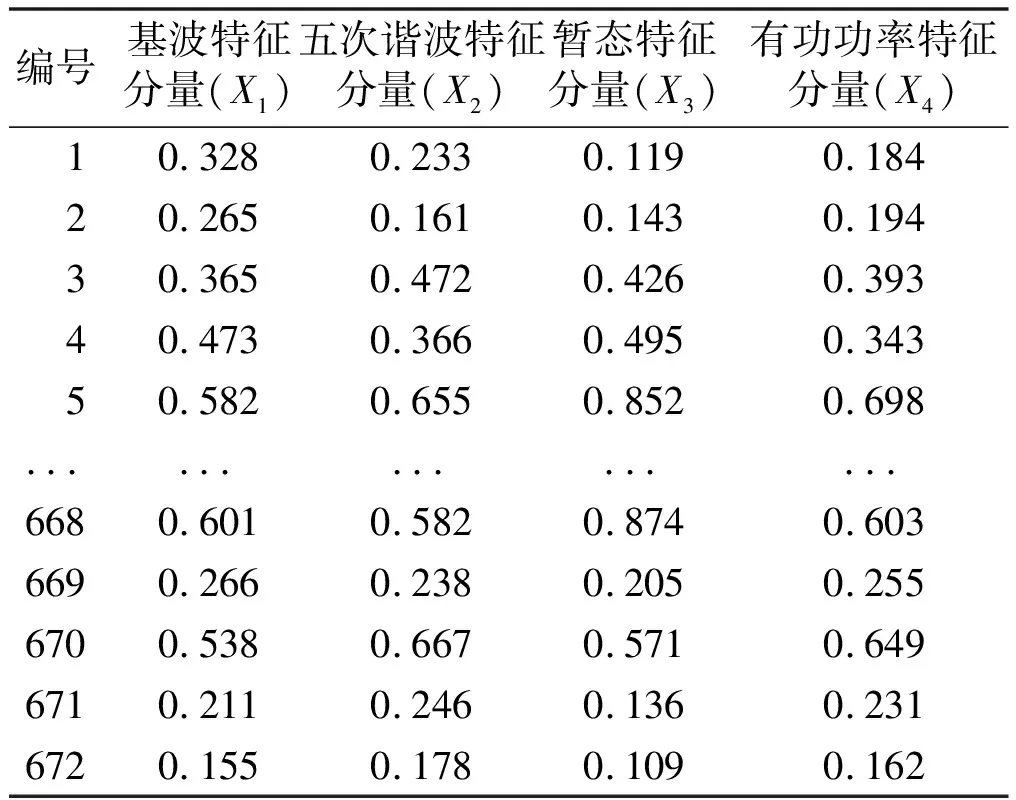
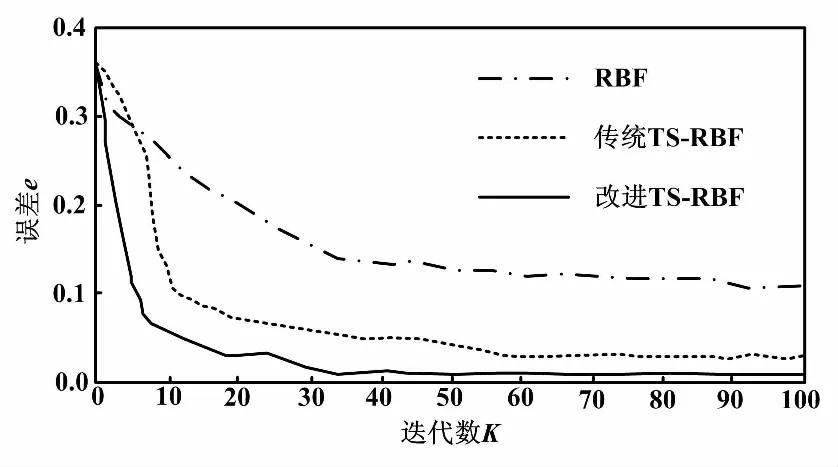
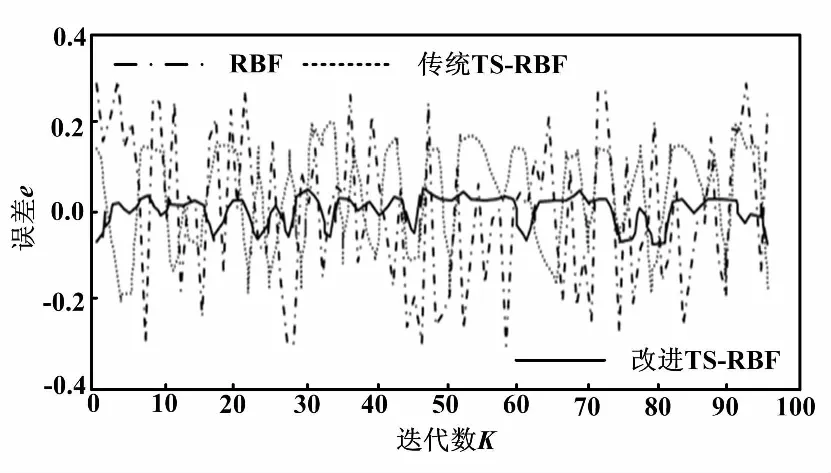
若f(Z) ④令X=Z,若所有点和步长都穷尽(B-J为空),则转步骤⑤;否则转步骤②。 ⑤若当前迭代周期内最优解精度低于上一周期(终止条件),则停止迭代;若不满足迭代终止条件,将禁忌表清空(J=0),转步骤②。 禁忌算法优化RBF网络的评价目标是适应度函数。本文适应度函数以误差平方和倒数的形式给出: (1) 改进禁忌算法优化RBF网络流程如图2所示。 图2 改进禁忌算法优化RBF网络流程图 首先,在单相接地发生时采集零序电流的稳态和暂态有效故障特征,以区别故障和正常线路。稳态电流的采样取故障发生三个周期后的信号,利用快速傅里叶变换算法(fast Fourier transform,FFT),得到零序稳态电流的有功分量、基波分量和5次谐波分量。对于暂态电流,则取故障前一周期和后一周期的信号,通过小波采样法进行分解。本文采用db10小波包5层分解,提取出暂态能量特征值。每条线路的零序电流稳态特征和暂态特征作为一组故障录入数据,构成神经网络训练和测试的样本。这些样本都经过归一化处理。 其次,根据禁忌算法训练神经网络的步骤,输入零序电流的稳态基波分量、5次谐波分量、有功分量及暂态能量特征分量,对神经网络的结构参数进行优化,最终得到RBF网络最佳的网络层连接权值、隐含层的中心和宽度等参数。 最后,将故障测试数据同时输入未经优化和优化后的RBF网络,比较二者的选线准确率和效率。多判据融合选线模型如图3所示。 图3 多判据融合选线模型 ATP系统仿真模型如图4所示。本文仿真模型为一个110 kV/35 kV的配电系统,变压器35 kV侧中性点经过一开关接消弧线圈。开关闭合与否构成中性点两种运行方式:不接地或经消弧线圈接地。低压侧共8条架空出线。线路长度为:L1=5 km,L2= 10 km,L3=25 km,L4=20 km,L5= 35 km,L6= 30 km,L7=15 km,L8=40 km。线路正序参数为:感抗L1=1.51 mH/km,电阻R1=0.17 Ω/km,容抗C1= 9.70 nF/km。线路零序参数为:感抗L0=5.48 mH/km,电阻R0=0.23 Ω/km,容抗C0=6.00 nF/km。采样周期设定为1×10-5s。 图4 ATP系统仿真模型 每条线路发生单相接地故障采集的故障特征分量为4个。一次性将8条线路共32个故障分量输入RBF网络,经网络计算后应得到8条线路的判断结果。RBF网络的输入输出容易决定,但中间隐含节点数直接影响网络预测精度与效率,节点数并非越多越好。隐含节点数超过某一数值后精度不再有明显变化,反而计算量会陡增。大量样本的仿真测试表明,隐含节点数取为58是合适的。据此,3层RBF神经网络的结构设为32-58-8。取768个样本中的672个作为训练样本,剩余96个作为测试样本。部分故障特征分量如表1所示。 表1 部分故障特征分量 禁忌搜索算法的参数设置如下:种群规模设为40,禁忌搜索迭代周期设为100,禁忌长度设为50,目标误差设为0.02。为了比较RBF、传统TS-RBF及改进TS-RBF这3种方法的选线效果,同时采用训练样本对3种网络进行训练。其目标是使网络输出的选线误差小于设定的目标误差。3种方法的网络训练误差曲线如图5所示。 图5 网络训练误差曲线 由图5可知,改进TS-RBF网络优化起始阶段的收敛速度明显快于RBF和传统TS-RBF网络,在迭代27次后即达到目标误差;而传统TS-RBF需要83次,RBF需要378次。同时,改进TS-RBF在收敛精度方面也明显优于其他两种方法。 对于3种训练好的网络,采用96个测试样本进行验证对比。网络输出接近1判定是故障线路,同时用网络输出与1的差值表达该网络对故障线路的逼近程度;同理,非故障线路的网络输出越接近0,则表示网络逼近精度越高。设定不同的试验条件(补偿度、短路点位置、合闸角和接地电阻),分别采用3种选线方法进行仿真试验,并比较3种算法的输出数值。对于正常线路,改进TS-RBF输出最逼近0,其次是传统TS-RBF,单纯RBF对0的偏差最大;对于故障线路,改进TS-RBF输出对1的偏差最小,其次是传统TS-RBF,单纯RBF偏差最大。从最终选线结果比较,共96个测试样本中单纯RBF出现8例误判,传统TS-RBF出现3例误判,而改进TS-RBF仅有1例误判。 3种网络的预测误差比较曲线如图6所示。 图6 3种网络的预测误差比较曲线 经统计:改进TS-RBF、传统TS-RBF和单纯RBF三者的选线准确率分别为98.9%、96.9%和91.7%,证实了改进TS-RBF的准确性。 鉴于RBF网络预测能力与其参数密切相关,本文应用改进的TS法优化RBF神经网络,优化误差曲线和最终选线结果都证实了改进TS-RBF网络相较于传统的TS-RBF,自学习能力和鲁棒性更强。 本文以110 kV/35 kV的配电系统作为仿真实例。为避免单一判据的误选和漏选,融合多种故障分量信息,实现对故障信号更精准的描述;结合改进的TS-RBF网络,构成多判据选线模型。仿真结果表明,该模型的选线准确率达到98.9%,且不受多种故障条件的干扰。
3 融合选线模型
4 仿真实例
4.1 系统建模

4.2 网络训练
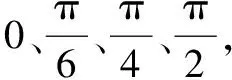
4.3 模型验证
5 结束语
