例谈“皮克定理”在高考中的考查
——数学文化原创题(四)
2019-12-20扬州市新华中学常国庆
扬州市新华中学 常国庆
近些年来,以数学文化为背景的高考题不断呈现,逐步形成了“依托数学史料,嵌入数学命题,彰显数学文化”的高考命题特色和亮点.
数学文化怎么考?数学文化题怎么解?这是同学们普遍关心的问题.
根据近些年的高考数学试卷分析,数学文化题是另一种形态下的常规题,同学们不必害怕,将它当作一道应用题来解就行了.如果了解试题的文化背景,将会缩短你的思维过程,解题也会更简洁.下面以“皮克定理”为例,说说数学文化在高考中的呈现方式.
问题1:图1中的每个小正方形面积都是1,那么图中S△ABC=?
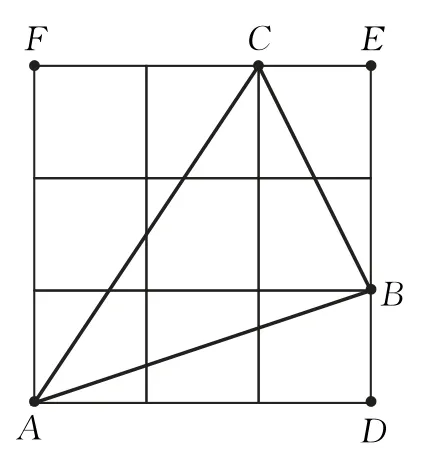
图1
问题2:如果给你一个不规则的任意多边形呢?割补起来就不那么简单了!
早在1899年,奥地利数学家乔治·亚历山大·皮克(GeorgAlexanderPick)发现,对于平面上的任意一个多边形,只要它的每一个顶点都在单位正方形网格的“格点”上,它的面积都有类似的巧算方法.皮克沿着这个思路进一步推导得到了一个超级简单的面积计算公式:记多边形内部所含的格点数为I,多边形边界上的格点数为B,则多边形面积这就是皮克定理.
一、皮克定理的证明
皮克定理的证明比较麻烦,这里先证明特殊情形(格点矩形、格点三角形)下的皮克定理,然后用归纳法证明一般情形(格点多边形)下的皮克定理.
1.格点矩形的皮克定理
证明:设矩形ABCD的长和宽分别是m和n,容易从图2上看出S=mn,I=(m-1)·(n-1),B=2(m+n),因为(n-1)+(m+n)-1=mn,所以
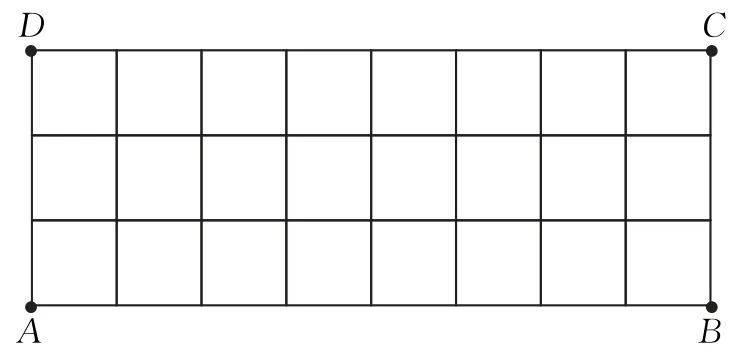
图2
2.格点三角形的皮克定理
证明:将三角形放置在矩形中,并使得矩形至少一个顶点与三角形的一个顶点重合.这样,格点三角形在矩形中有五种不同的情形,如图3:

图3
(1)证第①情形
如图3①设AB,BC,CA内含有的格点数分别为a,b,c,且因△ABC中有I个内格点,则矩形ABCD就有2I+c个内格点.故有

类似可证明②③④⑤情形.
3.格点多边形的皮克定理
证明:对于一个有k(k>3)条边的格点多边形.首先证明这样的多边形必有一条含于其内部的对角线.事实上,如果是凸多边形,则其结论是显然的;如果不是凸多边形,我们假定在某一顶点处P的内角大于180°,这时从P点出发的一条射线,让它扫过多边形内部时,必定会碰到另一个顶点(否则,多边形将会包围了一个面积为无穷大的区域),而这就决定了一条以P为端点位于多边形的对角线l.
现设格点多边形M有I个内格点和B个边界格点,而对角线l把M分成两个简单的格点多边形M1和M2,它们分别有I1和I2个内格点,B1和B2个边界格点,假定在l上除端点外有x个格点,则B=B1+B2-2-2x,I=I1+I2+x.
令S,S1,S2分别表示M,M1,M2的面积,则
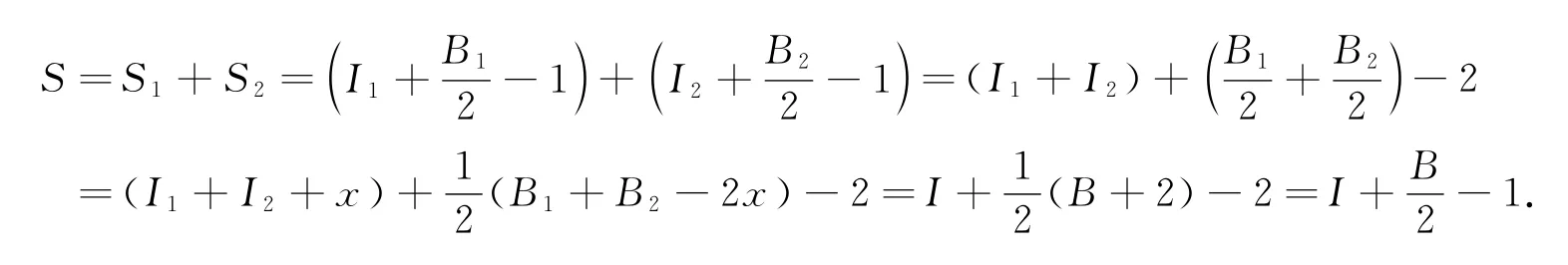
二、皮克定理的应用
1.高考试题中的皮克定理
例1(2013湖北文科卷)在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,则称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图4中△ABC是格点三角形,对应的S=1,N=0,L=4.
(1)图中格点四边形DEFG对应的S,N,L分别是_______;
(2)已知格点多边形的面积可表示为S=aN+bL+c,其中a,b,c为常数.若某格点多边形对应的N=71,L=18,则S=_______.

图4
例2(2011北京理科卷)设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为平行四边形ABCD内部(不含边界)的整点个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为( ).
A.{9,10,11} B.{9,10,12} C.{9,11,12} D.{10,11,12}
2.皮克定理的原创题
下面是新编的2道题,供大家练习.这两道题我们用常规方法都可以解决.相信你弄懂皮克定理内容后,可以有一个新的思路.毕竟多尝试一题多解,可以拓宽我们的思路啊!试一试用多种方法解决吧!
题1.不等式2x-3<y<3表示的平面区域内,正整数解的个数是_______个.
题2.在平面直角坐标系中,若P(x,y)的坐标x,y都是整数,则称点P为格点.直线x+y=n(n为正整数)与坐标轴围成的△ABC内包含有_______个格点,此时△ABC的面积为_______.
答案与解析:
题1.3.
分析:首先,将不等式2x-3<y<3转化为不等式组画出对应的平面区域,图5,然后在可行域中找出正整数点(1,1),(1,2),(2,2).
本题用皮克定理来解:S△ABC=9,而边界格点个数B=12,可得内格点个数I=4,而(1,0)不是正整数解,所以,正整数解的个数是3个.
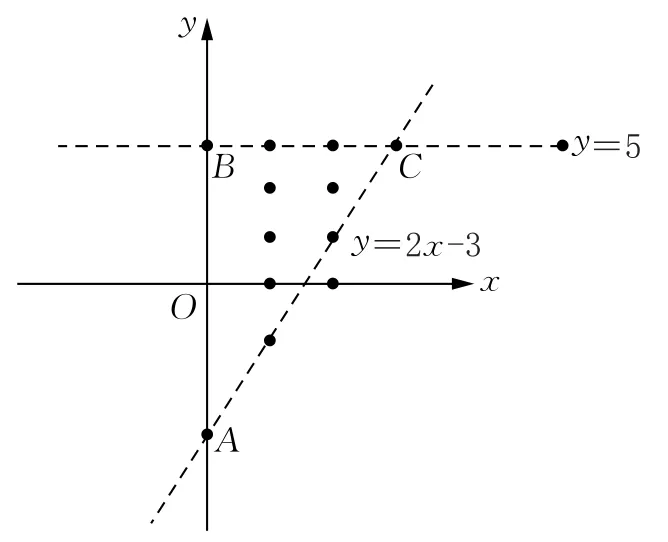
图5
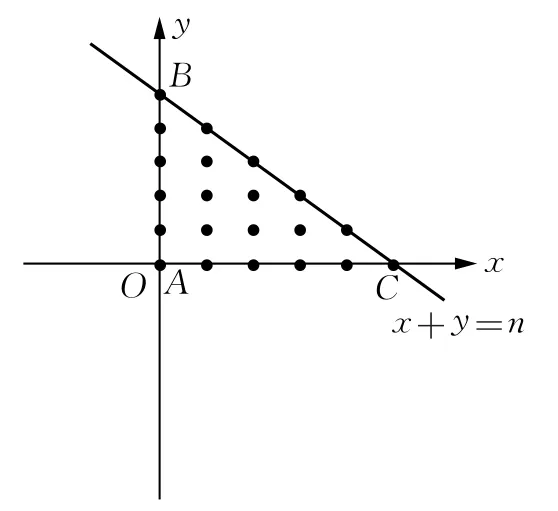
图6
题2.
分析:本题通过画图,如图6,结合数列知识,从特殊到一般归纳出△ABC内的格点个数为:
