滨海社区空间演变分形研究
——以厦门市高浦社区为例
2019-12-19俞晓牮赵志庆李焱龙
俞晓牮,赵志庆,李焱龙,林 松
(1.哈尔滨工业大学建筑学院、寒地城乡人居环境科学与技术工业和信息化部重点实验室,黑龙江 哈尔滨 150001; 2.闽南师范大学生物科学与技术学院,福建 漳州 363000; 3.厦门大学建筑与土木学院,福建 厦门 361005; 4.厦门大学海洋与地球学院,福建 厦门 361005)
随着党的十八大“建设海洋强国”与国家“十二五”规划“坚持海陆统筹”的提出,滨海城市纷纷将发展重点聚焦于沿海岸带区域。海洋经济发展使得我国沿海城市的空间结构演化具有与一般内陆城市不同的特征,正深刻改变着滨海城市的空间发展模式。因此,在城市化进程的探讨中,城市的空间形态演变规律对于统筹空间规划有重要的理论和实践意义。
分形理论最早是由曼德尔布洛特(1999)提出的,用以探讨英国的海岸线有多长[1]。分形几何跳出了传统欧式几何的整数维假设,成为描述复杂、不规则几何特征的主要工具,为滨海城市空间形态的复杂性研究提供重要的定量分析手段[2]。目前,我国学者对沿海城市海岸线分形特性开展了广泛的研究。李猷等(2009)以快速城市化地区深圳市为研究区域,系统分析了各时期海岸线时空动态演变特征[3]。张云等(2015)提取海岸线数据分析了海岸线长度历年变迁规律及分形维数的变化[4]。马小峰等(2015)利用分形维数理论对我国主要类型的海岸线进行了抽样分析,提出分形维数可作为衡量海岸带开发程度的量化指标[5]。尽管滨海城市拥有海岸线,然而当前城市分形理论与应用研究主要集中于非滨海城市的空间形态、结构以及演变规律[6-18]。Batty等(1994)利用分形维数来评价土地利用的不规则程度,并利用周长-面积法计算了英国Swindon市的土地利用形态[8]。Frankhauser(1998)发表了一系列中国城市的分形测算和分析结果[9]。Shen等(2002)计算了美国20个城市的分形维数,认为分形维数虽然可以作为衡量城市空间增长的指标,但是分形维数本身并没有说明城市形态的特定方向或者结构[10]。
滨海社区通常包括海岸线,具有复杂的系统特征[19-22]。近年来在快速城市化进程中,一些原本具有活力与特色的社区被快速城市建设吞没,逐渐沦为样态单一的城市组成单元。本研究从滨海社区分形方面进行研究,利用计盒维数对位于杏林海湾西畔的厦门高浦社区空间形态演变进行复杂性分析和分形维数计算。对该社区1989、2007、2017年的空间形态分形维与社区建筑总面积、建筑占地面积、容积率、建筑密度等指标的相关关系进行分析和比较。本研究旨在为滨海社区的系统开发提供重要理论依据和参考:一方面将复杂性分形理论应用于滨海城市社区研究,揭示滨海社区空间的分形特征;另一方面符合我国城市空间治理对支持理论的迫切需求,为制定社区城市化发展策略提供有价值的定量依据。
1 研究方法
1.1 分形理论
分形理论从传统欧式几何的整数维计算推广到一般维数的计算来测算分形对象,是研究不规则区域复杂特性的重要方法[1,6]。在欧式几何中,点是零维图形,线是一维图形,面是二维图形,而正方体是三维图形。一维图形满足
N=r-1
(1)
式(1)中:r是图形测量所需的标尺,N是所需标尺的数量。假设有一单位长度的线段,如果将其等分为N=2段,则每段长度为r=1/2;如果将其等分为N=3段,则每段长度为r=1/3,显然有N·r=1。类似的,单位面积的二维正方形满足
N=r-2
(2)
式(2)中:N·r2=1。如其等分为N=4份,则每一份边长为r=1/2的小正方形面积为r2=1/4;将其等分为N=9份,则每一份边长为r=1/3的小正方形面积为r2=1/9。
根据线段是一维的,平面是二维的,我们可以将(1)式与(2)式归纳得:
N=r-D
(3)
式(3)中:D代表维数,对(3)式两边取对数得:
(4)
然而对于某些图形而言,用式(4)计算所得的D并不是整数。例如著名的Koch曲线[1],可以通过图1a的迭代方式生成:平面上有一条单位长度的线段,将此线段分为3等份,拿去中间的1份,用去掉底边的边长为1/3的等边三角形连接此线段剩余的两部分,由此得到4份长度为1/3的线段所组成的折线,然后将这4条线段分别按照刚才的步骤进行操作,于是得到16条长度为1/9的线段所组成的折线,以此类推,可以得到第n次测量时标尺的长度r=1/3n以及所需标尺的数量N=4n,将其代入(4)式可得:
(5)
由此可见,Koch曲线的维数是一个介于1~2之间的常数,即为分形维数。
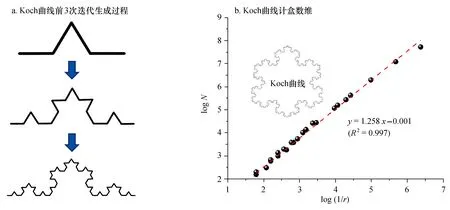
图1 Koch曲线前3次的迭代生成过程和计盒维数计算结果Fig.1 First three iteration of the Koch fractal curves and the calculated fractal dimension
1.2 计算方法及检验
分形维数的计算方法有很多,例如豪斯多夫(Hausdorff)维数、相似维数、计盒维数、容量维数、关联维数、信息维数等[1,17]。对于城市平面地图而言,把城市放在一个均匀分割的网格上进行覆盖,通过研究盒子覆盖数目与盒子半径的关系,可以求出分形维数[5]。这种计算盒数的方法由于其计算简单且有效,在城市分形研究中得到广泛应用。本研究采用计盒维数去计算社区空间和边界的分形维数,其算法是用边长为r的正方形去覆盖研究对象并且记录与研究对象相交的正方形盒子数量N,再代入式(4)中,当盒子边长r充分小时,则可以充分地接近研究对象的形态。在计算操作中,可以根据需要使用不同边长r的盒子去覆盖被测对象,得到一系列的盒子数量N与盒子边长r的数据对,然后采用log(1/r)为横坐标,以logN为纵坐标,在坐标系中描出一系列点[log(1/r), logN],最后采用最小二乘线性回归法去拟合这些点,求出斜率,而斜率就是该图形对应的计盒维数。
对于Koch曲线而言,用上述算法计算得到计盒维数为1.258(图1 b)。对比于理论值log4/log3,计算得到数值解仅有约0.30%的误差,表明了本研究分形维计算的可靠性。
对于社区空间形态而言,分形维数代表了空间图形的填充能力与不规则程度。若分形维数越高,则社区空间图形的填充能力也越强,社区边界相对会变得狭隘与曲折;相反,若分形维数越低,则空间图形的填充能力越弱,社区边界会变得简单与规整。为了检验计盒维数计算社区空间图形的有效性和误差,我们对边界平滑和区域填充的地图进行测试,如图2所示。根据式(2),对于完全填充的二维社区平面模型而言,其理论计盒维数应为2。而利用式(4)计算得到的维数为1.995(R2为0.999 9),相对于理论值的偏差为0.25%,这表明本研究的分形维数计算具有很高的数值精度。此外,根据式(1),对于社区边界光滑的一维曲线而言,其理论维数为1.000,而我们计算得到的维数为0.997(R2为0.999),相对于理论值的偏差为0.30%,进一步验证了本研究计算方法的可靠性。因此,能够利用计盒维数算法对高浦社区的分形特性进行定量计算和分析。
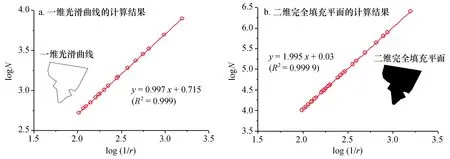
图2 计盒维数算法检验Fig.2 Numerical verification of box-counting dimension calculation
1.3 研究区域
1.3.1 区位 本研究以厦门市集美区杏林街道高浦社区为研究区域(图3)。高浦社区隶属于厦门市集美区杏林街道,位于杏林湾畔,杏林街道的东南部。社区南部临海,与高崎码头隔海相望,西至高浦路,北至杏林东路,东南至杏滨路。
1.3.2 社区现状 依托得天独厚的海湾型地理优势,高浦作为一个典型闽南小渔村,形成了滨海社区独特的海洋文化及空间特色。社区的发展与城市化海岸带的变化息息相关。随着厦门市加快海湾型城市建设和集美区加快城市化发展,特别是厦门岛内外一体化战略的实施,高浦社区的海岸带逐渐被破坏,社区当地原有的城市风貌、建筑、格局正慢慢消亡。社区人口结构、产业结构、高浦社区文化生态环境发生改变。
2 结果与讨论
2.1 研究数据的获取
本研究分析所用的数据主要包括建筑物轮廓以及建筑层数。使用的基础数据主要是厦门市地理信息中心所提供的1989年与2007年高浦社区的测绘AutoCAD地图,2017年所使用的AutoCAD地图是在社区实地调研的基础上对2007年的AutoCAD地图进行修测所得。
社区不同年代的地图是研究社区分形特性演变的关键图形信息。对于社区空间形态的提取首先需要将测绘的AutoCAD地图中其它测绘信息剔除,只保留建筑实体边线,然后等比例导出保存成为图片格式。再将导出的图片导入Matlab用户编写程序,提取建筑实体的边界然后进行填充,从而得到测算对象的整体空间形态平面图形。对于社区边界的提取则需要在AutoCAD软件中进行操作,依据的原则是社区最外围建筑的外边界以及建筑实体最外侧顶点的连线。
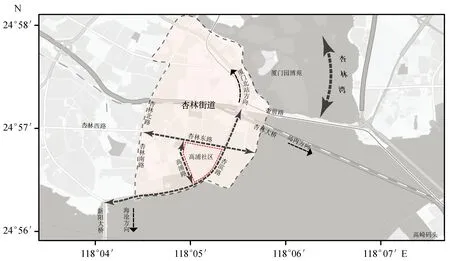
图3 高浦社区区位Fig.3 Location of Gaopu community in Xiamen
对于其它的建筑指标如社区建筑总面积(S1)、建筑占地面积(S2)、建筑用地面积(S3)、建筑密度,容积率等则需要在犀牛软件(Rhinoceros)中建立整个社区的建筑模型,然后再提取数据。建筑密度与容积率是非独立数据,需要利用公式获得。建筑密度指的是建筑占地面积与建筑用地面积的比值(S2/S3),衡量的是公共空间的疏密程度。例如一个小区的建筑密度为所有建筑的占地面积总和与整个小区范围用地面积的比值。而容积率指的是建筑总面积与建筑用地面积的比值(S1/S3),包含了层数的概念,衡量的是用地范围之内所容纳建筑空间量的大小。在相同建筑占地面积与相同的小区用地面积的情况下,建筑层数越高容积率就越大。在本研究中,社区建筑密度=社区建筑占地面积/社区土地使用面积;社区容积率=社区建筑总面积/社区土地使用面积。3个年份的社区土地使用面积则是分别根据图4中3个年份的社区边界来确定。
2.2 高浦社区空间形态的复杂性
图4对比了高浦社区在1989、2007、2017年的整体空间形态,呈现了从分散到充分填充的趋势。图5对比了这3个年份的高浦社区的边界形态,呈现了从不规则到规则的趋势。

图4 1989、2007和2017年高浦社区的整体及规则填充的空间形态Fig.4 Overall spatial patterns of Gaopu community in 1989, 2007 and 2017
基于图4和图5的空间形态,我们对这3个年份高浦社区的建筑规模进行了分析。从表1数据可以看出,这3个年份中社区建筑总面积、社区建筑占地面积都有着较大幅度的增加。但是社区建筑总面积的增幅要远大于社区建筑占地面积,1989—2007年这一阶段,社区建筑总面积增幅约为200%,社区建筑占地面积增幅为60%;2007—2017年这一阶段,社区建筑总面积增幅约为100%,社区建筑占地面积增幅为40%。这就表明建筑层数的增加幅度要远大于在社区空地上新增的建筑数量的增加幅度,也就是说社区中在原有宅基地的范围内对建筑进行加建或重建并增加层数的建设行为非常多,并且多于在社区中空地上的建设行为。此外,在社区空间规模扩张时,这3个年份的社区土地使用面积分别为0.30、0.46、0.51 km2。1989—2007年阶段,社区土地使用面积增幅约为53%;2007—2017年阶段,社区土地使用面积增幅约为11%,再结合当前社区现状可以判定高浦社区土地使用面积扩展的上限就是高浦路、杏林东路、杏滨路这3条城市主要干道所限定的范围,在未来的发展中基本没有再向外扩展的空间了。以社区土地使用面积为基础再结合建筑占地面积与建筑总面积,求得1989、2007、2017年的建筑密度分别是42%、46%、50%;容积率分别是50%、102%、140%。可以看到建筑密度与容积率的增幅都比较稳定,从而表明在高浦社区土地使用面积扩展的同时,社区内部公共空间被逐渐压缩。

图5 1989、2007、2017年高浦社区及平滑边界分布Fig.5 Smooth border distributions of Gaopu community in 1989, 2007 and 2017
表1 1989、2007、2017年高浦社区建筑用地相关指标和社区分形维结果
Tab.1 Relevant parameter and fractal dimension results of construction land of Gaopu community in 1989, 2007 and 2017

年份S1/m2S2/m2S3/m2建筑密度/%容积率/%整体分形维数边界分形维数198915291112733730281342501.731.332007469118212442461543461021.801.302017715761255487510524501401.831.27
2.3 高浦社区空间形态的分形计算与分析
为了定量描述社区形态的空间复杂性,图6给出了1989、2007、2017年高浦社区整体空间形态计盒维数的计算结果。求得这3个年份高浦社区空间形态的双对数log(1/r)和logN散点分布图,然后利用幂指数模型对其进行线性回归拟合。图6a-c中,log(1/r)与logN二者线性相关性显著(R2=0.999)。从表1可以看出,1989、2007、2017年高浦社区整体空间形态的分形维数分别为1.73、1.80、1.83,呈现增加趋势。图6得到的社区空间分形维随时间演变呈现非线性关系:
D=-218.943 703 647 602 18
+0.216 880 357 159 71×年份
-0.000 053 259 449 25×年份2
(R2=0.992)
(6)
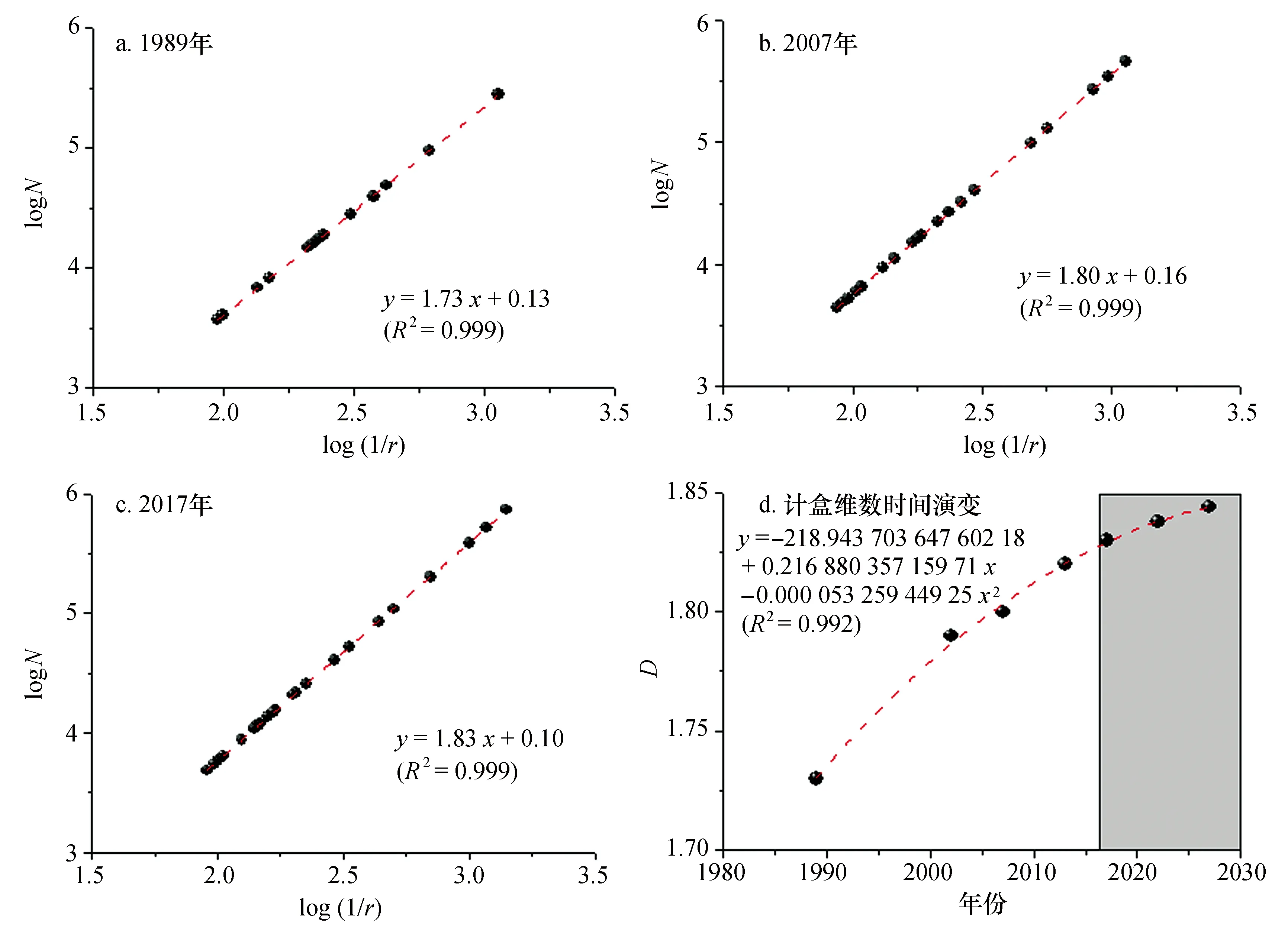
图6 1989、2007、2017年高浦社区空间形态的计盒维数结果及其时间演变Fig.6 Results of box-counting dimension for the overall spatial patterns of Gaopu community in 1989, 2007 and 2017, and the time evolution of the estimated dimension
高浦社区的复杂性还表现在分形边界上。图7为1989、2007、2017年高浦社区边界计盒维数的计算结果,这里所计算的边界指的是社区外边界。图7a、b中,[log(1/r),logN]的线性相关性显著(R2=0.999), 而图7c中,[log(1/r),logN]也显示显著的线性相关性(R2=0.998)。如表1所示,这3年社区边界分形维数为1.33、1.30和1.27,呈现减小态势。图7显示了社区边界分形维随时间演变呈非线性关系:
D=-285.241 178 271 465 51
+0.288 303 170 709 39×年份
-0.000 072 511 260 81×年份2
(R2=0.97)
(7)
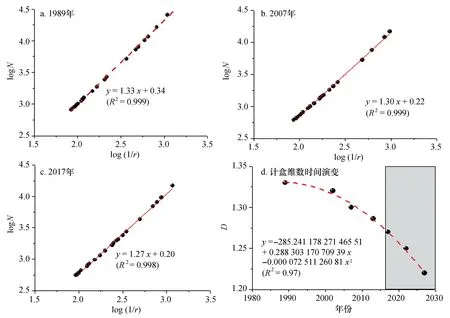
图7 1989、2007、2017年高浦社区边界的计盒维数结果及其时间演变Fig.7 Results of box-counting dimension for the border Distributions of Gaopu community in 1989, 2007 and 2017, and the time evolution of the estimated dimension
高浦社区的分形特性与社区建筑规模具有一定关联性。利用表1的数据,把计盒维数和建筑用地相关指标进行线性回归。表2给出了线性回归分析的结果,可以看出:社区整体分形维数与建筑占地面积、社区建筑总面积、社区建筑密度、社区容积率等建筑指标呈线性增长关系;然而,社区边界的分形维数与建筑占地面积、社区建筑总面积、社区建筑密度、社区容积率等建筑指标呈线性下降关系。这表明社区建筑规模的增加可能导致社区空间形态和边界复杂性发生变化。分形维数的变化和建筑实体对空间的填充能力与社区空间形态的不规则程度有关。空间复杂性的增加来自于建筑实体对空间的占据能力变强,受到建筑密度增加的影响。所以深入探究社区建筑规模指标和其复杂性之间的变化关系,有利于找出导致社区空间形态复杂性变化的主要原因,从而制定有效的社区改造方案。
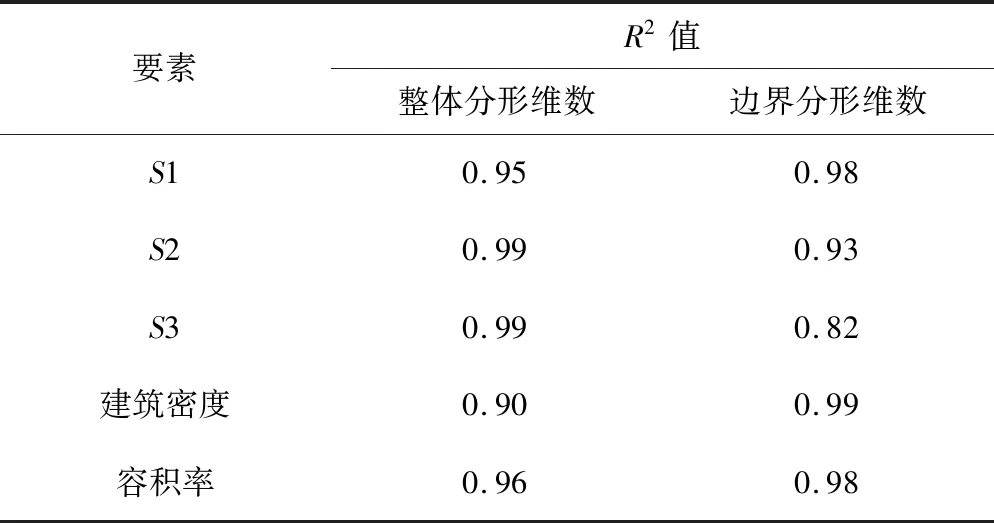
表2 高浦社区分形维数与建筑用地相关指标线性回归分析的R2值Tab.2 Linear regression analysis of fractal dimension and construction land factors of Gaopu community
2.4 讨论
高浦社区空间形态显示了多层次的复杂性(图4、5),主要体现在以下几个方面:①社区空间分布和边界体现了不规则性和复杂性。类似于分形海岸线(如英国、挪威等)[1,6,8],高浦社区的边界表现了一定程度的自相似性。高浦社区复杂的空间系统由成千上万个独立建筑个体组成,社区的进一步划分还能形成更小尺度的不规则邻里组团和公共空间分布等。高浦社区具有整体与局部的空间相似性,这种自我相似是分形的重要特性。②社区空间具有自然与人文双重属性。纵观高浦社区近30 a发展历程,社区空间受到三面环海的地缘因素影响。快速城市化发展给社区空间带来更多的变迁,当地原有的风貌、建筑、格局正慢慢消亡,社区内部的个体在一些政策与规范的影响下产生的相互作用与影响就直接或间接的表达在社区空间复杂形态的变化上[21-24]。③社区空间内部存在着复杂的经济和社会博弈过程。高浦社区作为城市居住空间,其最突出的特点应该是舒适性与公益性。然而在经济利益最大化的驱动下,社区内部的空间资源逐渐被压缩,边界被平滑,这种牺牲空间换取经济效益的行为屡见不鲜。社区空间的公益性、舒适性与经济效益之间的相互作用具有复杂性。这些因素在时间与空间上相互叠加,形成复合型社区的复杂系统。④社区空间蕴含着复杂的场所依赖或场所精神,即社区空间是一种物质-映像-行为的复合系统[25-26]。高浦社区的某些祠堂通常会成为邻里聚集、交流、娱乐的场所,而这些祠堂同时也向社区居民提供多层次、多结构的活动场所。可见,厦门市高浦社区有着鲜明的空间分布特色,其复杂系统与各层次子系统之间往往具有一定的自相似性,从而可以用分形理论来加以描述。
高浦社区的整体空间形态具有分数维数,表明其具有显著的分形特性(图6),为上述社区复杂性的定性分析提供了定量依据。在近30 a中,高浦社区整体空间形态的复杂性有所增加。社区空间形态分形演化的自相似性变化导致了复杂性变化,社区建筑逐步占据整个空间,而不断压缩剩余空间。本研究得到的社区分形维数小于2,揭示了社区建筑尚未占满整个二维空间,这与国内外对分形城市研究得到的结论相类似[9-18]。城市形态虽然具有分形特性,但是它的分形特性只存在于一定尺度或标度范围内。在二维空间中,大于1.9的城市形态都比较少见[10]。此外,本研究发现社区边界也具有分数维数(图7)。高浦社区整体空间形态的分形维数与社区边界的分形维数有显著的负相关性。表明在城市化过程中,社区边界变得更加规整,绿地与广场等公共空间的增加也会进一步导致社区边界的复杂性下降。高浦作为滨海社区包含海岸线和非海岸线部分。近年来的研究揭示了海岸线具有分形特性[1-5],那么高浦社区海岸线和非海岸线分形特性的比较值得进一步研究。
特别值得一提的是,本研究表明高浦社区整体空间和边界的分形维皆呈现非线性演变规律。采用式(6)进行计算,可以预测2022、2027年分形维数分别为1.838、1.844,表明社区整体空间形态的分形维数将逐渐提高,社区将被各种建筑填充,造成过度拥挤,而各层面的分形结构将被破坏。采用式(7)进行计算,可以预测2022、2027年分形维数分别为1.250、1.220,表明社区边界的分形维数随着年份呈下降趋势,边界分形特性将逐年受到破坏。尽管该预测有待于社区实际发展状况的检验,但社区复杂性的破坏、与海岸线相接区域的日益萎缩对有着深厚的文化底蕴与鲜明的地域特色的高浦社区极其不利,滨海社区空间的多样性和复杂性保护是十分必要的。
3 结论及展望
高浦作为厦门市杏林湾西畔的典型闽南小渔村,具有独特的海洋空间特色。近年来,随着厦门加快海湾型城市建设,高浦社区的海岸带和空间复杂性发生了改变。本研究通过对高浦滨海社区3个年份空间形态的分形特性研究,分析了社区在快速城市化的近30 a中空间复杂性的变化,并且初步揭示了社区复杂性的变化与社区建筑规模的扩张呈现出的相关性。研究结果表明:
(1)高浦社区空间形态和边界都呈现显著的分形结构特性,这证明了分形理论可以适用于滨海社区的复杂性研究。
(2)1989、2007、2017年社区空间形态的分形维数呈现增长态势,然而这3个年份社区边界的分形维数呈现减小态势。
(3)1989、2007、2017年社区建筑占地面积、建筑总面积、建筑密度、容积率与社区空间形态的分形维数表现出显著的正相关性,但与社区边界分形维数表现出负相关性。表明社区规模的扩张导致了社区复杂性的变化。
滨海社区分形研究尚有几方面问题需要讨论:①样本广泛性问题。滨海社区城市化演变研究需要在更长的时间尺度上,依赖于更多的样本,对所提出社区复杂性演变规律做进一步补充研究。②分形维数的变化与人口增长之间的相关性问题。例如外来人口的增多会带动社区内部私租房产业的活跃,进而促使社区居民房屋加建行为的增加,造成社区内部建筑密度继续升高。③分形维数的变化与滨海社区总的经济产值之间的相关性。海洋经济产值的结构在近30 a间的改变对社区空间复杂性的影响。
致谢:感谢厦门大学环境与生态学院李杨帆教授与广西大学资源环境与材料学院孙翔副教授对本研究的宝贵建议。
