尺规作图——过圆外一点作圆的切线方法归纳

胡小华

(江苏省南京市金陵中学河西分校 210036)

尺规作图是初中平面几何中的重要知识，是中考的热门题型，学生需综合运用所学的知识，多角度思考问题.在初三第一轮复习时，我设计了这样一个问题“过圆外一点A作⊙O的切线，尺规作图，保留作图痕迹，并说明作图的依据，比一比谁的画法多”.

学生作品展示

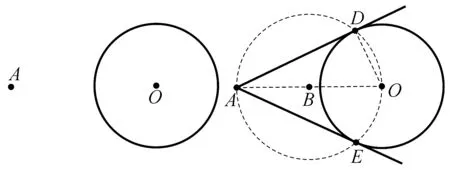
图1

方法一：利用直径所对的圆周角是直角.

连接AO，以AO为直径作⊙B，⊙B与⊙O相交于D、E两点，则AD，AE即为所求作的切线.

理由：⊙B中∵AO是直径，

∴∠ADO=90°即OD⊥AD.

∵AD经过半径OD的外端,

∴AD与⊙O相切.

图2

该方法是由切线想到垂直，构造直角的常用方法之一是利用直径所对的圆周角是直角这一定理.再由切线的判定方法：过半径外端，并且垂直于半径的直线是圆的切线.切线的作法即转化为主要考虑作半径的垂线的方法，联系初三刚学过的知识，我们首先想到的是直径所对的圆周角是直角这一定理，这一方法也就顺其自然而产生.

方法二：利用“等腰三角形三线合一”的性质作垂直.

以O为圆心，BC长为半径作弧，以A为圆心，AO长为半径作弧，两弧交于点D，OD与⊙O相交于点E，连接AE，则AE即为⊙O的切线.另一条切线也可以用同样的方法作出.

理由：∵AO=AD,

OD=BC=2OE,

∴E为OD的中点.

∴AE⊥OD,

∴AE与⊙O相切.

要作切线想到垂直，而利用等腰三角形三线合一的性质也是我们常见的构造垂直的方法之一.

方法三：利用勾股定理的逆定理构造垂直.

分析：先假设切线画出来了，则斜边长为AO长，一条直角边长为半径r，根据勾股定理可以求出另一条直角边的长.

图3

作∠DCH=90°，在CH上截取半径r，交CH于点G，以G为圆心,AO长为半径作弧，交CD于点F，则CF长即为所求作的切线长.

以A为圆心，CF长为半径作弧交圆O于点E，连接AE，则AE即为所求作的一条切线.

理由：∵∠C=90°,

∴FC2+CG2=FG2.

又∵AO=FG,CG=OE,FC=AE,

∴AE2+OE2=AO2.

∴AE⊥OE,

∴AE是⊙O的切线.

图4

该作图方法是利用勾股定理的逆定理构造直角，想法比较独特，通过先构造直角找到三边关系，再利用三边关系构造直角，从而创造切线.学生的思维让人眼前一亮.

方法四：利用相似作垂直证半径.

延长AO到D，使得OD=OA.以D为圆心，以⊙O直径长为半径作弧，以O为圆心，OA长为半径作圆，交弧于点F，连接AF.过O点作OE⊥AF，交AF于点E，则AE即为所求作的切线.

证明：∵AD为直径,

∴∠AFD=90°.∵OE⊥AF,∴OE∥DF,

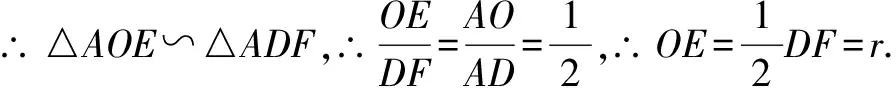
前三种方法均是连半径，作垂直，第四种方法是作垂直证半径，刚好复习了初中阶段的证明切线的两种方法，也是学生综合运用知识解决问题能力的一种体现.

在复习期间这样一个开放性的问题激发了学生学习的热情和潜能，围绕数学问题展开的思维碰撞，无不是学生学习主动性、能动性和创造性的综合体现.在解决问题的过程中复习了初中阶段常见的构造垂直的几种重要方法，我不禁感叹“只要给学生一个舞台，他们必将还我一片精彩”！