自寻优最近邻算法估算有限气象数据区潜在蒸散量

冯克鹏，田军仓，洪 阳

自寻优最近邻算法估算有限气象数据区潜在蒸散量

冯克鹏1,3,5，田军仓1,3,5※，洪 阳2,4

（1. 宁夏大学土木与水利工程学院，银川 750021；2. School of Civil Engineering and Environmental Science, University of Oklahoma，Norman, OK 73072, USA；3. 宁夏节水灌溉与水资源调控工程技术研究中心，银川 750021； 4. 北京大学遥感与地理信息系统研究所，北京 100084；5. 旱区现代农业水资源高效利用教育部工程研究中心，银川 750021）

FAO-56 Penman-Monteith估算ET0方法被广泛使用，但计算时需要输入多个气象数据。开发一种替代方法，在使用尽可能少的气象数据情况下，仍可以提供准确的或至少接近FAO-56 Penman-Monteith的ET0估算值是该领域研究热点之一。该文结合典型相关分析（canonical correlation analysis，CCA）和最近邻算法（-nearest neighbor，-NN），提出自寻优最近邻算法的潜在蒸散量计算方法（CCA--NN），利用较少气象数据实现潜在蒸散量的估算。核心思想是用CCA算法寻找与潜在蒸散量最相关的气象数据，实现后续估算ET0时的气象数据降维，然后利用-NN算法估算ET0。选择西北地区为例，将该区域气象数据分别从时间和空间尺度，分为训练数据集，验证数据集和测试数据集，分别在3类数据集上用该文方法估算ET0，并以FAO-56 Penman-Monteith作为参照，评估了该文CCA--NN方法的估算精度和适用性。结果表明，CCA--NN方法与FAO-56 Penman-Monteith保持了较高的相关性（相关系数大于0.9），有好的估算精度，均方根误差和平均绝对误差均小于1 mm/d，空间尺度上算法纳什效率系数均大于0.5，时间尺度上纳什效率系数均大于0.8，在时空尺度均适用。同时，相对于其他替代方法该文算法具有低的时间复杂度，在计算大量数据时可有效降低时间成本。

蒸散量；相关分析；气象数据；最近邻算法；西北地区

0 引 言

蒸散发是水循环过程重要的组成部分之一。准确估算蒸散发，对作物灌溉、灌区用水调度、流域水资源管理、生态环境评估、不同尺度水资源平衡研究以及水文、生态系统模型建模都是必须且极其重要的。到目前为止，学者们提出了20余种蒸散发估算方法。这些方法可分为3类：基于温度的估算方法（Hargreaves-Samani、Thornthwaite等方法），基于辐射的估算方法（Priestley-Taylor、Turc等方法）和组合方法（Penman-Monteith，PM；Kimberly-Penman等方法）。这些方法都需要输入气象观测数据[1]。PM方法以能量平衡和水汽扩散理论为基础，同时考虑了作物的生理特征和空气动力学参数变化，能适应于不同气候地区。它被联合国粮农组织（food and agriculture organization of the united nations，FAO）推荐为标准ET0估算方法（FAO-56 PM），在世界范围内被广泛应用，也常作为标准参照方法来验证其他ET0估算方法的适用性[2]。然而，由于PM方法估算ET0时，需要输入较多的气象观测数据，这造成该方法在一些发展中国家或观测设备不具备地区难以适用[3]。其他基于温度或辐射的方法，需要输入的数据少，但正是因为所用数据少，不够全面，导致它们估算的ET0精度较低。因此，学者们一直致力于开发一种替代方法，在使用尽可能少的气象数据情况下，与上述传统方法相比，该替代方法仍可以提供准确的或至少接近FAO-56 PM的ET0估算值。

随着机器学习技术和人工智能的兴起，学者们开始探索如何将智能算法和传统估算方法结合，准确有效地估算ET0。1998年Tahir等学者将人工神经网络算法（artificial neural network，ANN）用于蒸散发预测，随后众多学者用4～7种气象及其他辅助数据作为输入，围绕ANN及其衍生算法估算ET0开展了一系列研究[4-8]，研究结果表明基于ANN的估算模型可有效地估算ET0，比基于温度或辐射的方法估算结果更优。近年来，也有学者利用多于5种以上的气象数据，通过Bayesian方法[9]，多变量相关向量机（multivariable relevance vector machine，MVRVM），多层感知机（multilayer perceptron，MLP）以及最小二乘支持向量机算法（least-square support vector machines，LSSVM）估计ET0，结论表明上述方法可满足ET0估算的需要，MVRVM较MLP有很好的稳定性和鲁棒性[10]，最小二乘支持向量机的ET0计算模型，其模拟精度高于Hargreaves公式和Priestley-Talor公式[11]。

从2014年至今，学者们在机器学习算法中深耕，挖掘其在ET0估算中的潜力。一个方向是以多种气象数据作为输入（多于5种），评估多个机器学习算法估算ET0的性能。主要的结论包括：遗传算法，极限学习机和广义回归神经网络方法ET0均优于Hargreaves、Priestley-Taylor、Makkink及Irmark-Allen等经验方法[12-14]。模糊逻辑（fuzzy logic）和支持向量回归（least squares support vector regression，LS-SVR）方法能够较好地利用现有的气候数据对日蒸发过程进行建模[15]。ANN算法ET0预测性能比-SVR算法更有效[16]。LSSVM，MARS和M5 Tree 3种算法估算月尺度ET0时，LSSVM算法在测试期具有最小的相对误差[17]。另一个方向是不断尝试用新机器学习算法估算ET0。王升等以5个气象要素作为输入，建立基于基因表达编程（gene expression programming，GEP）智能算法的ET0估算模型，其估算结果与FAO-56 PM估算值非常接近，比传统的Hargreaves and Samani、Irmak以及Turc方法精确[18-19]。也有学者考虑到输入数据较多，尝试通过主成分分析（principal component analysis，PCA）进行数据降维（7种降到5种），再结合ANN算法估算ET0，该方法在节省计算时间成本的同时保持了估算的精度[20]。

上述研究运用机器学习算法，为准确估算ET0开辟了诸多有效的路径。但存在2方面可提高之处：1）这些机器学习算法的时间复杂度较高。如简单3层ANN算法的时间复杂度为(2)，朴素贝叶斯算法的时间复杂度为(3)，支持向量机SVM的时间复杂度为(2)，支持向量回归算法SVR和最小二乘支持向量机的时间复杂度可达到样本数的3次方，即(3)。时间复杂度表示了执行某个算法所需要的计算工作量。可见，当需要估算的ET0样本数增加时，上述算法的时间成本相当高。2）前人运用机器学习算法估算ET0时仍需要较多的气象数据作为输入。因此，本文尝试使用尽可能少的气象数据，运用低时间复杂度的机器学习算法，建立准确估算ET0的方法。为了评估本文方法估算ET0的精度和效用，选择中国西北地区作为案例，将估算结果同FAO-56 PM对比，研究本文所提出方法的适用性。

1 材料与方法

1.1 研究方法

1.1.1 FAO-56 Penman-Monteith算法

本文训练样本数据集中的ET0由FAO-56 PM算法估算而得，其定义如下[21]：

式中ET0为潜在蒸散量，mm/d；R为输入冠层净辐射量，MJ/(m2·d)；为土壤热通量，MJ/(m2·d)；为干湿温度计常数，kPa/℃；2为2 m高处风速，m/s；e为饱和水汽压，kPa；e为实际水汽压，kPa；为日平均温度，℃；D为饱和水汽压与温度关系曲线在某处的斜率，kPa/℃。

1.1.2 典型相关分析算法

典型相关分析（canonical correlation analysis，CCA）是通过计算2组随机向量的交叉协方差矩阵分析相关性。

设：

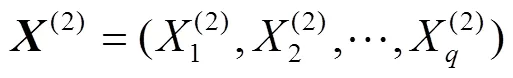
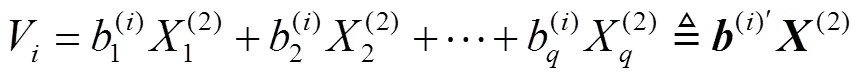
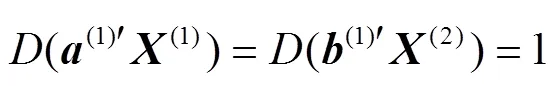
1.1.3最邻近算法

最邻近算法（-nearest neighbor，-NN）是机器学习技术中一种非参数惰性监督分类算法，原理简单且易于代码实现，算法时间复杂度只有()。算法的核心思想是对于一个新输入的数据，计算给定训练样本数据集中每个样本与新输入数据的距离，按照距离递增排序并找到与该新输入的数据最相近的个样本，最后在这个样本数据中统计样本占多数的类别，则新输入的数据就属于该类别[26-28]。

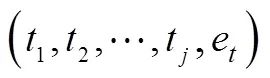
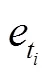
2）计算新输入气象数据，与所有训练样本数据集中样本之间的近似程度。通常，这个近似程度用欧氏距离，曼哈顿距离等方法来定量描述。本文选用了最易于理解且复杂度低的欧式距离，它来源于欧氏空间中2点间距离公式

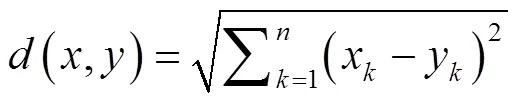
式中为样本间距离，x和y是分别来自新输入气象数据和训练样本数据集的样本。

计算出所有样本距离之后，按照距离递增排序，找出与该新输入气象数据最相近的个样本。

需要注意的2个方面：①是-NN算法中，属于超参数，不同值对算法结果有较大影响[29]。若选择较小值，则只有与输入数据最近的少量训练样本形成最终的预测，易导致过拟合。若选择较大值，则有较多的训练样本对预测结果产生贡献。其优点是一定程度上可减少估算误差，但缺点是会导致样本近似误差增大，使得与输入数据距离较远的训练样本也会对估算起作用。因此，在实际应用中，需要进行值优选。②是在计算输入数据与训练样本之间的距离之前，应对特征向量进行归一化处理。因为，不在同一值域的特征向量对距离计算产生的影响是显著的，较大值域的特征在计算距离的过程中，使算法忽略其他小值域的特征，这会降低估算的准确度。

1.1.4 有限气象数据CCA-NN潜在蒸散量估算方法构建

本文尝试用尽可能有限的气象数据作为输入，运用时间复杂度低的机器学习算法，建立较准确估算ET0的方法。上述2个基本机器学习算法尚不能直接用来估算ET0，还需要建立一个机制将二者有机耦合，协同工作，构建能够较准确估算ET0的方法。核心思路是：通过CCA找出与ET0最相关的气象要素，然后用少量最相关气象要素作为输入，通过NN算法估算ET0。其中，在-NN估算ET0之前对特征向量进行归一化；在估算过程中，初始化值范围，建立迭代器，并通过性能评估指标，自动逐步寻找最优值；最后按照最优值完成ET0估算。方法流程图如图1所示。

注：k为适宜的样本数。

1.2 评估指标

本文选用5种统计评估指标：相对偏差（Bias），均方根误差（root mean square error，RMSE），平均绝对误差（mean absolute error，MAE），相关系数（correlation coefficient，CC）以及Nash-Sutcliffe纳什效率系数（Nash-Sutcliffe coefficient of efficiency，NSCE），用于值优选以及定量评估本文CCA--NN估算方法相较于FAO-56 Penman Monteith的估算精度。

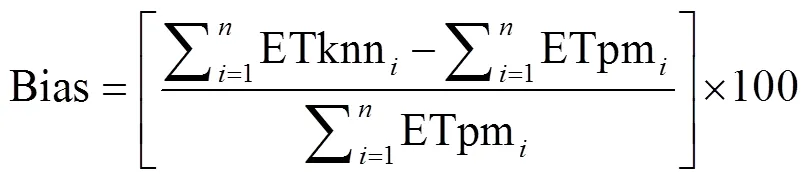
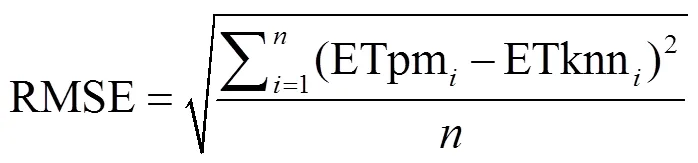
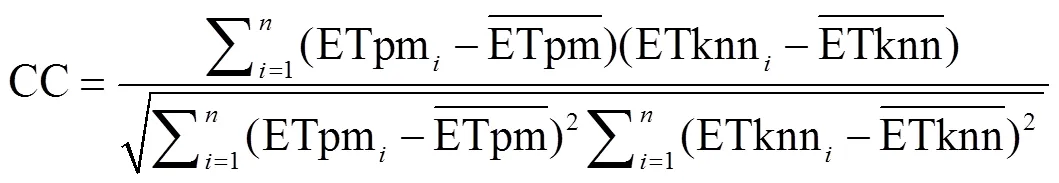
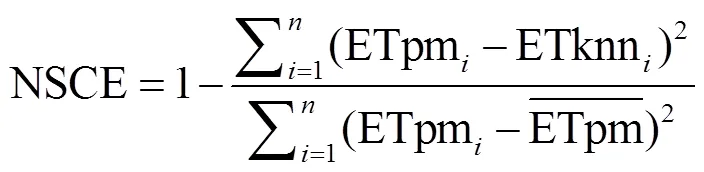
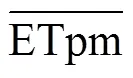
1.3 研究区域与数据

本文选择中国西北地区作为案例，检验本文CCA--NN潜在蒸散量估算方法的适用性。西北地区地域辽阔，行政区划包括陕西﹑甘肃﹑宁夏﹑青海﹑新疆以及内蒙古的一部分，其地域面积约占中国总国土面积的1/3。该区域内干旱、半干旱、半湿润气候并存，山峦、戈壁、绿洲、荒漠等地形地貌交织，生态脆弱，对气候变化敏感性高。选择该区域有利于评估本文算法在气候多样性和下垫面条件复杂区域的ET0估算性能。

本文采用中国气象局气象数据中心（http://data.cma.cn/）提供的西北地区184个气象站的日尺度平均最高气温、平均最低气温、平均气温、日照时数、平均风速以及平均相对湿度6种气象数据。对该数据进行预处理，舍弃数据缺失严重的站点，进行均一化，气候界限值、异常值，台站极值等检查，并根据检查结果对数据进行了必要的插补和订正。经过以上步骤，得到148个气象站1960－2018年完整的气象数据。

为了从时间和空间2个角度，评估本文CCA--NN潜在蒸散量估算方法的适用性，将上述数据在时空尺度上分别分为3部分。其中，空间尺度上是将全部148个气象站点中60%的站点（89个）作为训练数据集，30%的站点作为验证数据集（44个），运行经过训练的模型，剩余10%的站点（15个）作为测试数据集。时间尺度上，将1960－2018共59 a的数据，前60%的年份（1960－1994，35a）作为训练数据集，中间30%的年份（1995－2012年，18a）作为验证数据集，其余10%的年份（2013－2018年，6年）作为测试数据集。训练数据集用于训练模型，找出最佳的超参数，验证数据集用于确定模型超参数，测试数据集用于对训练好的参数和算法进行性能评估。

研究区域内气象台站分布见图2。表1提供了西北地区1960—2018年气象数据从时空2种尺度划分为3类数据集的统计参数：日平均风速，日平均最高气温，日平均最低气温，日平均气温，日照时数，日平均相对湿度。

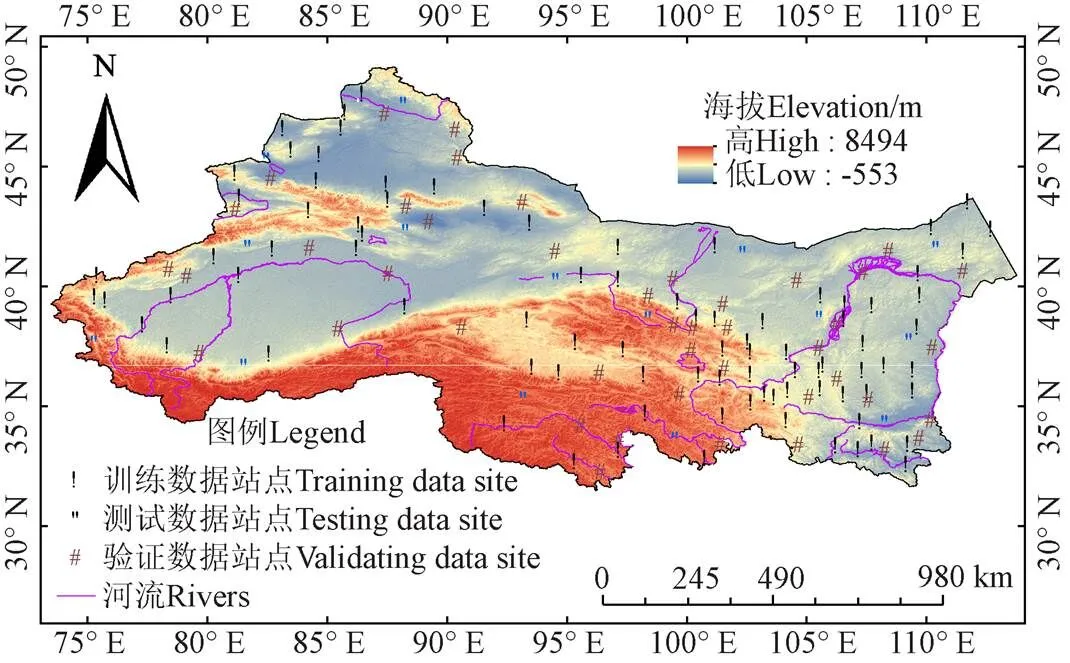
图2 研究区域内气象站点分布

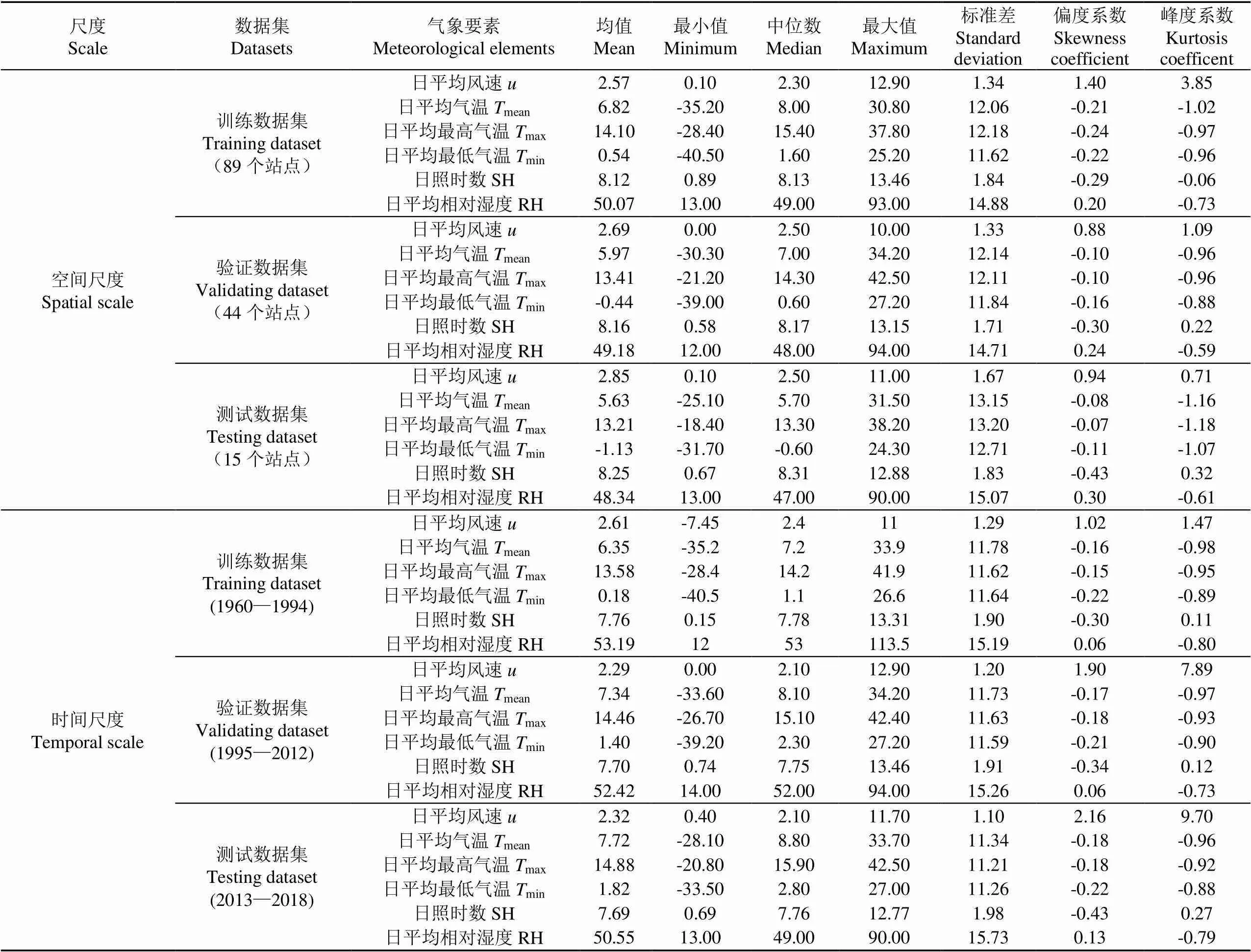
表1 西北地区1960－2018年气象数据时空尺度划分不同数据集的统计参数

注：对于均值、最小值、中值、最大值，气温的单位均为℃；日照时数单位为h，风速单位为m·s-1，相对湿度单位为%。

Note: For mean, minimum, median and maximum values, unit of air temperature, sunshine hours, wind velocity and relative humidity are ℃, h, m·s-1and %, respectively.

2 结果与分析

2.1 与ET0最相关气象要素

本文在训练样本数据集上，运用CCA算法，从风速，平均气温，最高气温，最低气温，日照时数和相对湿度中（这6项气象数据是FAO-56 PM方法计算ET0时的常规输入数据项），提取与ET0最相关气象要素。CCA算法在训练样本数据集上找到了一个典型相关变量，记为。典型变量与ET0的相关系数达到0.975，且通过了0.01水平的显著性检验。

由图3可知，原变量与之间有很好的相关性，按相关系数绝对值将相关性从高到底排序，依次是最高温度，相对湿度，平均温度，风速，最低温度，日照时数。因此，本文选取最高气温和相对湿度作为西北地区与ET0最为相关的气象要素。

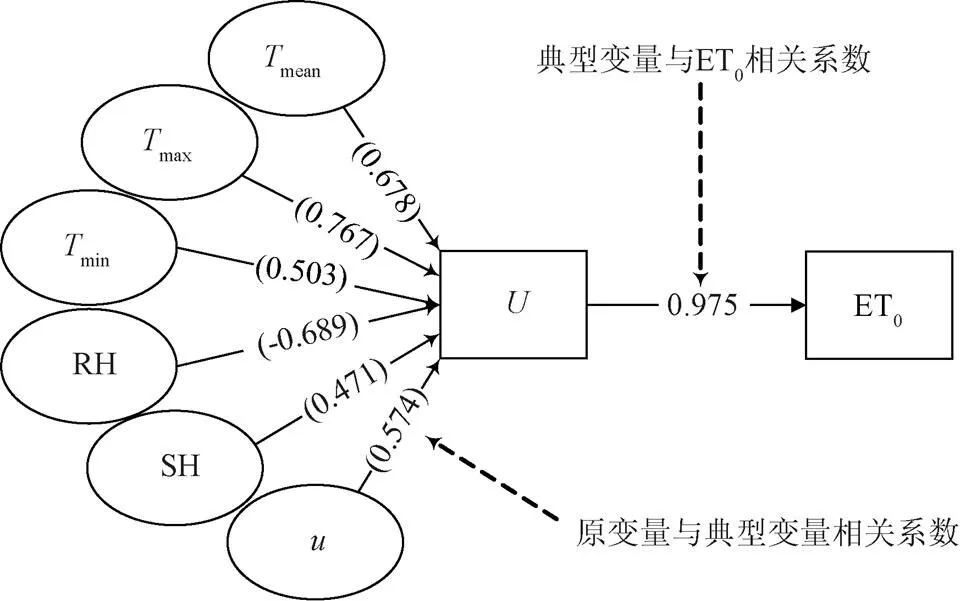
图3 气象要素与ET0相关系数结构图

2.2 k值优选

在训练数据集上以最高气温和相对湿度作为输入，运用-NN算法进行ET0估算。如前文所述，值对估算结果优劣影响较大。因此，在进行最终估算之前，需要优选出西北地区各气象站的值。设值范围为1～200，初始值为1。将不同值估算的ET0同FAO-56 Penman Monteith估算结果对比，以相关系数CC≥0.9，NSCE≥ 0.50作为值优选迭代的收敛条件。西北地区各气象站的优选值如图4所示。

由图4可知，优选的值分布在值域为[15，32]的区间；从空间分布角度观察，值呈现一定的地域相似分布规律，尤其在陕西，内蒙古，宁夏，甘肃地区较为明显。

得到各气象站点优选值后，分别在时间和空间尺度的训练数据集，验证数据集以及测试数据集上，以最高气温和相对湿度作为输入，运用-NN算法进行ET0估算，并将估算结果与FAO-56 Penman Monteith结果对比。通过对训练数据集上的结果分析，判断是否找出了最佳的超参数，验证数据集上的结果分析用于确定模型超参数，最后用测试数据集上的结果分析对CCA--NN算法进行整体性能评估。

图4 西北地区各气象站的优选k值空间分布

2.3 时间尺度CCA-k-NN潜在蒸散量估算方法的性能

将CCA--NN潜在蒸散量估算方法在时间尺度不同数据集上的估算结果同FAO-56 Penman Monteith结果对比，评估本文方法在时间尺度上的适用性。如图5和表2所示，本文CCA--NN方法在时间尺度的训练数据集上得到的ET0估算结果，与FAO-56 PM计算结果具有高的相关性，相关系数CC分别达到了0.921，且通过了0.05水平的显著性检验，这说明本文优选的超参数值是最佳的。验证数据集上本文算法估算结果同与FAO-56 PM计算结果的相关系数为0.906，结果略有低估，这可能由近邻样本加权平均误差造成。

本文估算结果与FAO-56 PM计算结果的RMSE和MAE误差分别为0.851、0.652 mm/d，良好的统计结果也进一步说明该超参数值合理。再将优选的超参数应用于测试数据集，其结果相关系数为0.905，在0.05水平显著相关；Bias指标为2.33%，尽管相对于前2个数据集略有增大，但RMSE和MAE误差均不足1 mm/d；NSCE指标为0.834，达到了优秀级别。

综上，整体观察本文CCA--NN潜在蒸散量估算方法在上述3个数据集上的表现，说明该方法在时间尺度上是适用的，超参数的优选值以及算法的设计是可行的。

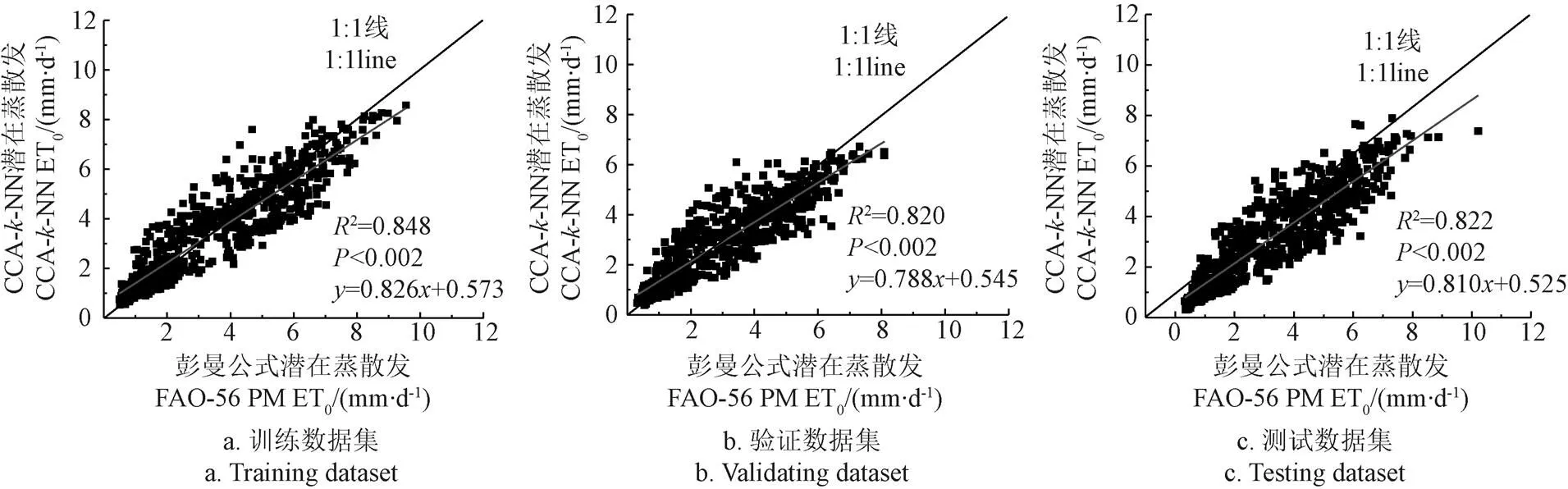
图5 CCA-k-NN ET0估算方法在时间尺度不同数据集同FAO-56 PM对比

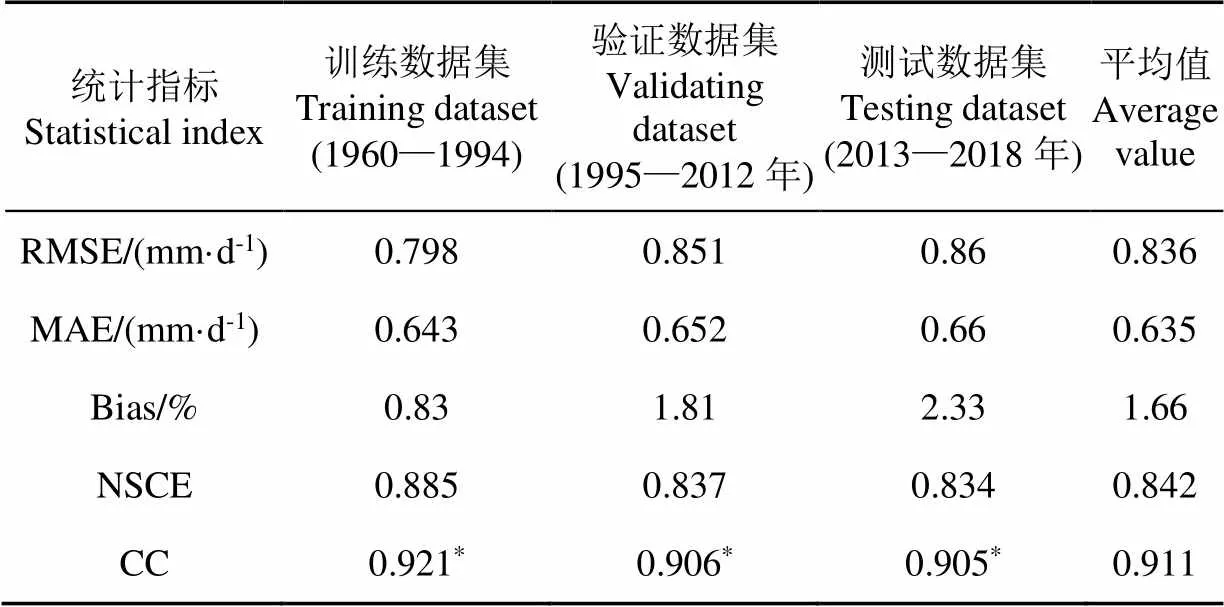
表2 时间尺度上CCA-k-NN潜在蒸散量估算方法性能统计

注：*，<0.05。CC，相关系数。下同。

Note: *,<0.05. CC is correlation coefficient, same as below.

2.4 空间尺度CCA-k-NN潜在蒸散量估算方法的性能

图6和图7描述了在空间尺度不同数据集上本文算法的估算性能。

如图6所示，本文CCA--NN ET0估算方法同FAO-56 Penman Monteith结果在空间尺度训练数据集和验证数据集上有高的相关性，相关系数都大于0.9；线性拟合线接近于45°直线，斜率接近于1，截距只有0.5左右，接近于0。结合表3对估算误差的统计，本文CCA--NN ET0估算结果的RMSE在训练数据集上为0.847 mm/d，验证数据集上为0.830 mm/d；MAE分别为0.637、0.632 mm/d；Bias在验证数据集上相较于训练数据集略大，但也只有1.28%。由此说明本文CCA--NN ET0方法的估算结果与FAO-56 Penman Monteith非常接近。

图6 CCA-k-NN ET0估算方法在空间尺度不同数据集上同FAO-56 PM对比

a. 训练数据集a. Training datasetb. 验证数据集b. Validating datasetc. 测试数据集c. Testing dataset

表3 空间尺度上CCA-k-NN潜在蒸散量估算方法性能统计

Table 3 Performance statistics of CCA-k-NN potential evapotranspiration estimation method on spatial scale

注：训练数据集有89个站点，验证数据集有44个站点，测试数据集有15个站点。

Note: The training dataset has 89 sites, the verification dataset has 44 sites, and the testing dataset has 15 sites.

观察NSCE效率系数（图7a和图7b），无论在训练数据集还是验证数据集，NSCE都大于0.5，即都达到“适用”及以上。其中，在训练数据集89个站点中，达到“适用”的站点有5个，“良好”7个，“优秀”77个，占比分别为5.6%，7.9%，86.5%。在验证数据集44个站点中，达到“适用”的站点有1个，“良好”11个，“优秀”32个，占比分别为2.3%，25%，72.7%。

为进一步验证本文CCA--NN ET0估算方法在空间尺度的适用性，在训练及验证数据集之外，选择15个独立气象站点（随机选择但在西北整个地区空间近似均匀分布）作为测试数据集，分别用本文算法和FAO-56 Penman Monteith估算ET0，并对估算结果进行评估，如图7c所示。

在测试数据集上，本文CCA--NN ET0估算结果同FAO-56 Penman Monteith结果非常接近，相关系数达到0.912。根据表4对估算误差的统计，RMSE为0.823 mm/d，MAE为0.621 mm/d，Bias为1.77%。在全部15个气象站点，NSCE效率系数达到“适用”的站点1个，“良好”4个，“优秀”10个，占比分别为6.6%，26.7%，66.7%。可见，本文CCA--NN ET0估算方法，在测试数据集上保持了稳定性，由此也表明该方法的空间适用性。

3 结 论

本文提出了一种基于自寻优最近邻算法的潜在蒸散量计算方法（canonical correlation analysis--nearest neighbor CCA--NN），利用与ET0最相关的2个气象要素实现了潜在蒸散量的估算，并选择中国西北地区作为检验算法适用性的案例，将该区域的气象数据分别从时间和空间尺度，分为训练数据集、验证数据集和测试数据集，在时空尺度上用本文算法估算ET0，并将估算结果同FAO-56 Penman Monteith估算结果对比，其结果接近FAO-56 Penman Monteith方法估算结果，相关系数大于0.9，均方根误差和平均绝对误差均小于1 mm/d，空间尺度上算法纳什效率系数均大于0.5，时间尺度上NSCE均大于0.8。结论显示本文方法无论在时间尺度还是空间尺度都是适用的。

[1] Nema M K, Khare D, Chandniha S K. Application of artificial intelligence to estimate the reference evapotranspiration in sub-humid Doon valley[J]. Applied Water Science, 2017, 7(7): 3903－3910.

[2] Manikumari N, Murugappan A, Vinodhini G. Time series forecasting of daily reference evapotranspiration by neural network ensemble learning for irrigation system[C]// IOP Conference Series: Earth and Environmental Science. Tamil Nadu: IOP Publishing, 2017: 012069.

[3] Yassin M A, Alazba A A, Mattar M A. Modelling daily evapotranspiration using artificial neural networks under hyper arid conditions[J]. Pakistan Journal of Agricultural Sciences, 2016, 53(3):695－712.

[4] Tahir S. Estimating Potential Evaporation Using Artificial Neural Network[M]. Notes. Jakarta: INACID, 1998: 1－12.

[5] 郑重，马富裕，李江全，等. 基于BP神经网络的农田蒸散量预报模型[J].水利学报，2008(2)：230－234.

Zhen Zhong, Ma Fuyu, Li Jiangquan et al. Forecast model for field evaportranspiration based on BP ANN[J] Journal of Hydraulic Engineering, 2008(2): 230－234. (in Chinese with English abstract)

[6] Kumar M, Bandyopadhyay A, Raghuwanshi N S, et al. Comparative study of conventional and artificial neural network-based ET0estimation models[J]. Irrigation Science, 2008, 26(6): 531－537.

[7] Landeras G, Ortiz-Barredo A, López J J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain) [J]. Agricultural water management, 2008, 95(5): 553－565.

[8] Huo Z, Feng S, Kang S, et al. Artificial neural network models for reference evapotranspiration in an arid area of northwest China[J]. Journal of Arid Environments, 2012, 82: 81－90.

[9] Hern S, Morales L, Sallis P. Estimation of reference evapotranspiration using limited climatic data and Bayesian model averaging[C]// 2011 UKSim 5th European Symposium on Computer Modeling and Simulation. IEEE, 2011: 59－63.

[10] Torres A F, Walker W R, McKee M. Forecasting daily potential evapotranspiration using machine learning and limited climatic data[J]. Agricultural Water Management, 2011, 98(4): 553－562.

[11] 侯志强，杨培岭，苏艳平，等. 基于最小二乘支持向量机的ET0模拟计算[J]. 水利学报，2011，42(6)：743－749.

Hou Zhiqiang, Yang Peiling, Su Yanping, et al. Simulation of ET0based on LS-SVM method[J]. Journal of Hydraulic Engineering, 2011, 42(6): 743－749. (in Chinese with English abstract)

[12] 江显群，陈武奋. BP神经网络与GA-BP农作物需水量预测模型对比[J]. 排灌机械工程学报，2018，36(8)：762－766.

Jiang Xianqun, Chen Wufeng. Comparison between BP neural network and GA-BP crop water demand forecasting model[J]. Journal of Drainage and Irrigation Machinery Engineering, 2018, 36(8): 762－766. (in Chinese with English abstract)

[13] 冯禹，崔宁博，龚道枝，等. 基于极限学习机的参考作物蒸散量预测模型[J]. 农业工程学报，2015，31(增刊1)：153－160.

Feng Yu, Cui Ningbo, Gong Daozhi, et al. Prediction model of reference crop evapotranspiration based on extreme learning machine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(Supp1): 153－160. (in Chinese with English abstract)

[14] 冯禹，崔宁博，龚道枝，等. 利用温度资料和广义回归神经网络模拟参考作物蒸散量[J]. 农业工程学报，2016，32(10)：81－89

Feng Yu, Cui Ningbo, Gong Daozhi, et al. Modeling reference evapotranspiration by generalized regression neural network combined with temperature data[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(10): 81－89. (in Chinese with English abstract)

[15] Goyal M K, Bharti B, Quilty J, et al. Modeling of daily pan evaporation in sub tropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS[J]. Expert Systems with Applications, 2014, 41(11): 5267－5276.

[16] Tezel G, Buyukyildiz M. Monthly evaporation forecasting using artificial neural networks and support vector machines[J]. Theoretical and Applied Climatology, 2016, 124(1/2): 69－80.

[17] Kisi O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and M5 model tree[J]. Journal of Hydrology, 2015, 528: 312－320.

[18] 王升，陈洪松，聂云鹏，等. 基于基因表达式编程算法的参考作物腾发量模拟计算[J]. 农业机械学报，2015，46(4)：106－112.

Wang Sheng, Chen Hongsong, Nie Yunpeng, et al. Simulation of reference evapotranspiration based on gene-expression programming method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(4): 106－112. (in Chinese with English abstract)

[19] Mattar M A. Using gene expression programming in monthly reference evapotranspiration modeling: A case study in Egypt[J]. Agricultural Water Management, 2018, 198: 28－38.

[20] Adnan M, Latif M A, Nazir M. Estimating evapotranspiration using machine learning techniques[J]. International journal of Advanced Computer Science and Applications, 2017, 8(9): 108－113.

[21] Allen R G, Pereira L S, Raes D, et al. FAO Irrigation and drainage paper No.56[J]. Rome: Food and Agriculture Organization of the United Nations, 1998, 56(97): e156.

[22] 冯克鹏. 宁夏水资源优化配置决策支持系统研究[D]. 银川：宁夏大学，2014.

Feng Kepeng. Research on Decision Support System for Optimal Allocation of Water Resources in Ningxia[D]. Yinchuan: Ningxia University, 2014. (in Chinese with English abstract)

[23] Lai P L, Fyfe C. Kernel and nonlinear canonical correlation analysis[J]. International Journal of Neural Systems, 2000, 10(5): 365－377.

[24] Lin Z, Zhang C, Wu W, et al. Frequency recognition based on canonical correlation analysis for SSVEP-Based BCIs[J]. IEEE Transactions on Biomedical Engineering, 2006, 53(12): 2610－2614.

[25] Cherry S. Singular value decomposition analysis and canonical correlation analysis[J]. Journal of Climate, 1996, 9(9): 2003－2009.

[26] 毋雪雁，王水花，张煜东. K最近邻算法理论与应用综述[J]. 计算机工程与应用，2017，53(21)：1－7.

Wu Xueyan, Wang Shuihua, Zhang Yudong. Survey on theory and application of k-Nearest-Neighbors algorithm[J]. Computer Engineering and Applications, 2017, 53(21): 1－7. (in Chinese with English abstract)

[27] Xue K, Li Q, Xu H, et al. Vibration-based terrain classification for robots using-nearest neighbors algorithm[J]. Journal of Vibration Measurement & Diagnosis, 2013, 33(1): 88－92.

[28] Paolino J P. Using the rasch model and k-nearest neighbors algorithm for response classification.[J]. Journal of Applied Measurement, 2016, 17(2): 185.

[29] 李晓瑜. K近邻协同过滤推荐算法中的最优近邻参数[J]. 计算机与数字工程，2018，46(8)：1525－1528，1619.

Li Xiaoyu. Optimal neighbor parameter of k-nearest neighbor algorithm for collaborative filtering recommendation[J]. Computer and Digital Engineering, 2018, 46(8): 1525－1528, 1619. (in Chinese with English abstract)

[30] Moriasi D N, Arnold J G, Van Liew M W, et al. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations[J]. Transactions of the ASABE, 2007, 50(3): 885－900.

Method for estimating potential evapotranspiration by self-optimizing nearest neighbor algorithm

Feng Kepeng1,3,5, Tian Juncang1,3,5※, Hong Yang2,4

(1.750021,; 2.,,73072,; 3.750021,; 4.,100084,; 5.,750021,)

The FAO-56 Penman-Monteith method for estimating potential evapotranspiration is widely used, but multiple meteorological data are required. In this study, the potential evapotranspiration calculation method (CCA--NN) of self-optimizing nearest neighbor algorithm combining the canonical correlation analysis algorithm and the k-nearest neighbor algorithm was proposed to estimate potential evapotranspiration by using less meteorological data. This study chose the northwest China as a case. In this area, the arid, semi-arid and semi-humid climates coexist, and the topography of the mountains, Gobi, oasis, and desert are intertwined, it is ecologically fragile, and highly sensitive to climate change. Meteorological data included daily average wind speed, daily average maximum temperature, daily average minimum temperature, daily average temperature, sunshine hours, daily average relative humidity of 148 meteorological stations. They were divided into training datasets, verification datasets and test datasets. On the spatial scale, 60% of all 148 meteorological sites (89 sites) were used as training data sets, 30% of sites were used as verification data sets (44 sites) and the remaining 10% of sites (15 sites) as the test dataset. On the time scale, the data of 1960-2018, the first 60% of the period (1960-1994) was as the training data set, the middle 30% of the year (1995-2012) was as the verification data set and the remaining 10% of the year (2013-2018) was as a test data set. For the training sample dataset, the most relevant meteorological elements in Northwest China with potential evapotranspiration were the highest temperature and relative humidity using typical correlation algorithms. Then, the highest temperature and relative humidity were used as input for the model. The optimal k value was selected by iteration and the results showed that the k value (15-32) of each weather station in northwestern China was suitable. Then, the verification data set and the test data set were respectively input with the highest temperature and relative humidity and the k nearest neighbor algorithm was used for potential evapotranspiration estimation. Models were evaluated by using relative deviation, root mean square error, mean absolute error, correlation coefficient and Nash-Sutcliffe efficiency coefficient. The results showed that the CCA--NN method maintained a high correlation with the FAO-56 Penman-Monteith (correlation coefficient greater than 0.9), with good estimation accuracy, and the root mean square error and the mean absolute error were less than 1 mm/d. On the spatial scale, the Nash efficiency coefficient of the algorithm was greater than 0.5, and the Nash efficiency coefficient on the time scale was greater than 0.8, which was applicable at both space and time scales. At the same time, the algorithm had low time complexity compared to other alternative methods, and could effectively reduce the time cost when calculating large amounts of data.

evapotranspiration; correlation analysis; meteorological data;nearest neighbor algorithm; northwestern China

冯克鹏，田军仓，洪 阳. 自寻优最近邻算法估算有限气象数据区潜在蒸散量[J]. 农业工程学报，2019，35(20)：76－83.doi：10.11975/j.issn.1002-6819.2019.20.010 http://www.tcsae.org

Feng Kepeng, Tian Juncang, Hong Yang. Method for estimating potential evapotranspiration by self-optimizing nearest neighbor algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(20): 76－83. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.20.010 http://www.tcsae.org

2019-04-11

2019-09-10

宁夏自然科学基金（2019AAC03049）；国家重点研发计划项目（2018YFC0408104）；国家自然科学基金（51869024）；宁夏高等学校一流学科建设项目（NXYLXK2017A03）；宁夏重点研发计划重大项目（2018BBF02022）；宁夏高等学校科研项目（NGY2017026）

冯克鹏，副教授，博士，主要从事气候变化与水文水资源研究。Email：fengkp@nxu.edu.cn

田军仓，博士，博士生导师，主要从事水资源高效利用研究。Email：slxtjc@163.com

10.11975/j.issn.1002-6819.2019.20.010

P426.2

A

1002-6819(2019)-20-0076-08