图的1-因子数目的递推求法

唐保祥，任韩

（1.天水师范学院 数学与统计学院,甘肃天水 741001；2.华东师范大学数学系,上海200062）

0 引言

图的1-因子计数问题已被证明为NP-难问题[1]。但有许多图可通过递推得到它们的1-因子数目的递推关系式，有些还可解出其通解，从而得到对应图1-因子的计数公式[2-11]。因此，递推法是求解图的1-因子数目的一种重要方法。

1 基本概念

定义1若图G有一个1-正则生成子图，则称此生成子图为图G的1-因子。图G的1-因子也称完美匹配。

定义2设图G是一个有1-因子的图，若图G的2个1-因子M1和M2中有一条边不同，则称M1和M2是G的2个不同的1-因子。

定义3长为n的2条路为P1=u0u1u2…un和P2=v0v1v2…vn,ui与vj连接一条边当且仅当|ij|=0或2(i,j∈ {0,1,2,…,n})，这样得到的图记为Wn,2，见图1。

定义4设Ci=ui1ui2ui3ui4ui5ui6ui1是长为6的圈(i=1,2,…,n)，给圈Cj与圈Cj+1加 上 边uj1uj+1,6,uj2uj+1,5,uj3uj+1,4(j=1,2,…,n-1)得到的图记为3-nC6，见图2。

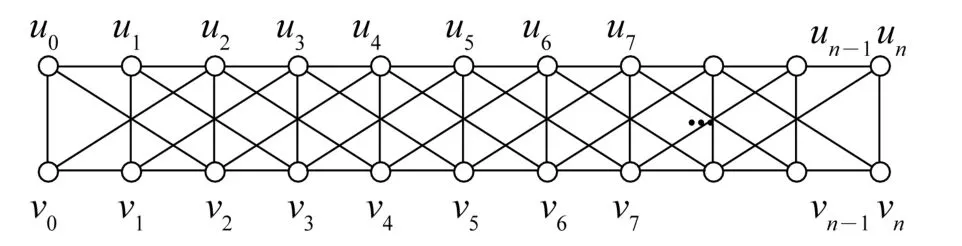
图1 Wn，2图Fig.1 Figure of Wn，2

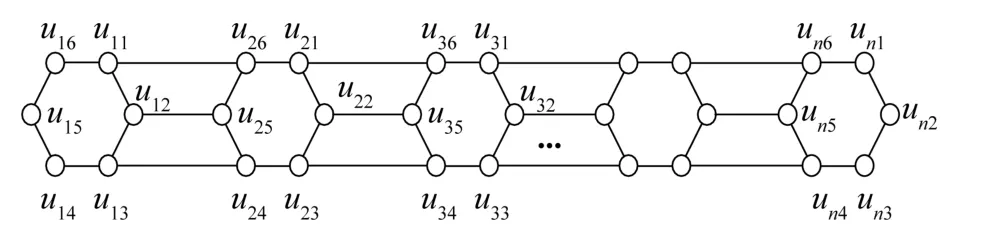
图2 3-nC6图Fig.2Figure of 3-nC6

2 主要结果及其证明

定理1 设图Wn,2的1-因子数为f(n)，则

其中，c1,c2,c3,c4为以下线性方程组的解：

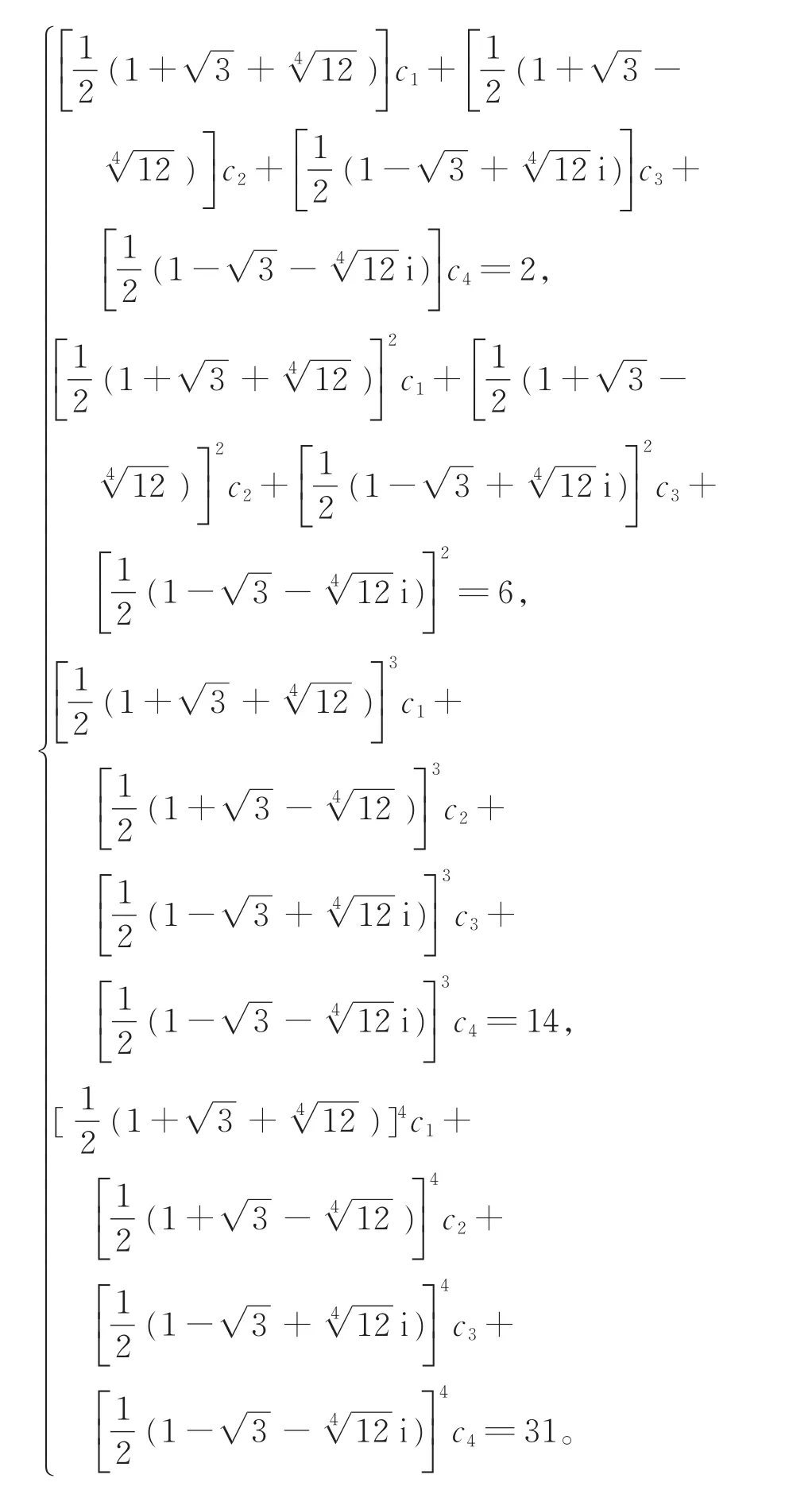
证明 显然图Wn,2有1-因子。为求f(n)的递推式，先定义2个图G1和G2，并求出它们的1-因子数的递推关系式。将路xy的端点x和y分别与图Wn,2的顶点v0和u0各连接一条边，得到的图记为G1，见图3。

图3 G1图Fig.3 Figure of G1

将路xy的端点x与图Wn,2的顶点u0连接一条边，端点y分别与图Wn,2的顶点u1和v0各连接一条边，得到的图记为G2，见图4。

显然图G1和G2都有1-因子，设g(n),h(n)分别表示图G1和G2的1-因子的数。

图4 G2图Fig.4 Figure of G2

首先求g(n)的递推式。设图G1的1-因子的集合为M，G1的包含边xy,xv0的1-因子的集合分别为M1,M2,则M1∩M2=∅,M=M1∪M2,故|M|=|M1|+|M2|。

由f(n)的定义知，G1的包含边xy的1-因子数等于f(n)，即|M1|=f(n)。

因为xv0∈M2,所以yu0∈M2,从而xy,u0v0,u0u1,u0v2,v0v1,v0u2∉M2,所以由f(n)的定义，|M2|=f(n-1)。故

其次求h(n)的递推式。设图G2的1-因子的集合为M(1)，图G2包含边xu0,xy的1-因子的集合分别为M3，M4，则M3∩M4= ∅，M(1)=M3∪M4，

h(n)= ||M(1)=|M3|+|M4|。

求 |M3|。因为xu0∈M3，所以xy，u0v0，u0u1,u0v2∉M3。因此，由h(n)的定义,有

求 |M4|。因为xy∈M4，所以xu0，yu1，yv0∉M4,因此，由f(n)的定义，有|M4|=f(n)。

综上所述，

最后求f(n)的递推式。设图Wn,2的1-因子的集合为M(2)，图Wn,2包含边u0v0,u0v2,u0u1的1-因子集合分别为M5,M6,M7，则

Mi∩Mj=∅,5≤i＜j≤7，

M(2)=M5∪M6∪M7，

故f(n)=|M(2)|=|M5|+|M6|+|M7|。

求 |M5|。因为u0v0∈M5,所以u0u1，u0v2，v0v1,v0u2∉M5,由f(n)的定义知，

求|M6|。分2种情形。

情形1若u0v2,v0u2∈M6,则u0v0，u0u1，u1u2，u2u3,u2v2,u2v4,v0v1,v1v2,v2v3,v2u4∉M6。因此,由g(n)的定义，M6中包含边u0v2,v0u2的1-因子数为g(n-3)。

情形2若u0v2,v0v1∈M6,则u0u1，u0v0，u1v1,v0u2,v1v2,v1u3,v2v3,v2u4,u2v2∉M6。因此，由h(n)的定义，M6中包含边u0v2,v0v1的1-因子数为h(n-3)。

M6中，上述2类1-因子互不包含、互不相交，且穷尽了M6中所有1-因子，故

求 |M7|。因为u0u1∈M7,所以u0v0，u0v2，u1v1,u1u2,u1v3∉M5,由g(n)的定义知，

综上所述，

将式 (1)和(2)代入式 (3)，得

由式 (4)，得

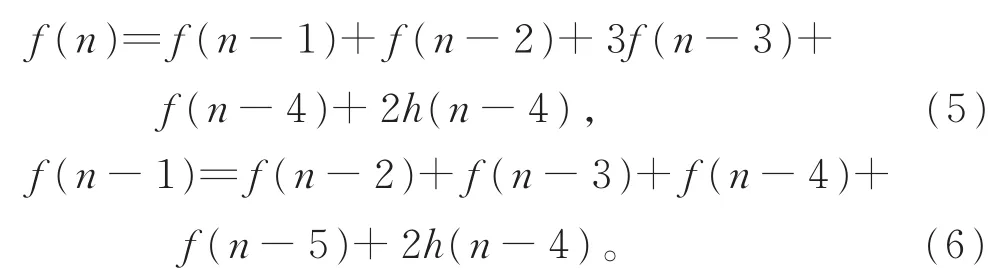
式 (5)- 式 (6)，得

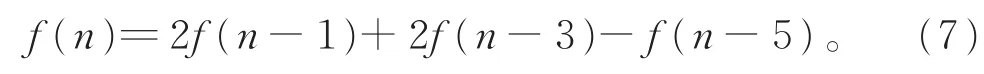
线性递推式(7)的特征方程为

显然，在此方程中，x≠0,方程两边同除以x,得

所以f(1)=2,式(7)的通解为

由f(n)的定义，易得图5～图8。

图5 G3图Fig.5 Figure of G3

由图5易知，f(2)=6。

图6 G4图Fig.6 Figure of G4

图7 G5图Fig.7 Figure of G5

由图6和图7知，g(1)=3,h(1)=4,

图8 G6图Fig.8 Figure of G6

由图8(图中带波浪线的为1-因子中的边，虚线不是)知，

f(3)=6+2+2+2+2=14。

所以f(4)=f(3)+g(1)+h(2)+h(1)=14+3+10+4=31。

故c1,c2,c3,c4由以下方程组确定：

定理2设图3-nC6的1-因子数为σ(n)，则σ(n)=2 ·3n-1。

证明易知图3-nC6有1-因子。为得到σ(n)的递推式，定义图G7,并求出其1-因子的递推式。将路pq的端点p,q分别与图3-nC6的顶点u15,u14连接一条边，得到的图记为G7,见图9。

图9 G7图Fig.9 Figure of G7

设τ(n)表示图G7的1-因子的数，图G7的1-因子的集合为M(3)，图G7包含边pq，pu15的1-因子集合分别为M8，M9，则M8∩M9=∅，M(3)=M8∪M9，故

τ(n)=|M(3)|=|M8|+|M9|。

因为pq∈M8,所以pu15,qu14∉M8,故由σ(n)的定义知，|M8|=σ(n)。

因为pu15∈M9,所以qu14,u16u11∈M9,且pq,u15u14,u15u16,u11u12,u11u26∉M9,故由τ(n)的定义知，|M9|=τ(n-1)。因此,

再求σ(n)的递推式。设图3-nC6的1-因子的集合为M(4),图3-nC6包含边u16u11,u16u15的1-因子集合分别为M10，M11，则M10∩M11=∅，M(4)=M10∪M11，故

σ(n)=|M(4)|=|M10|+|M11|。

因为u16u11∈M10,所以u15u14∈M10,且u16u15,u11u26,u11u12,u14u13∉M10,故由τ(n)的定义知，|M10|=τ(n-1)。

因为u16u15∈M11,所以u14u13∈M11,且u16u11,u15u14,u13u12,u13u24∉M11,故由τ(n)的定义知，|M11|=τ(n-1)。因此,

将式 (10)代入式 (11)，得

由式 (11)和(12)得

σ(n)=3σ(n-1)=3n-1σ(1)。

显然σ(1)=6,故σ(n)=2 ·3n-1。

3 总 结

能求出递推关系式的图很多，但由递推式解出其显式表达式的图则有限，原因是当递推式对应的特征方程为高次时，往往无法求得其根。但从应用角度看，图的1-因子数的递推式往往比其显式表达式更易得到其1-因子数。比如，本文图1的1-因子数目的显式表达式很复杂，但其1-因子数却很容易由递推式求得。