Experimental and numerical investigation of threedimensional vortex structures of a pitching airfoil at a transitional Reynolds number

Zhenyo LI, Liho FENG, Hmid Rez KARBASIAN, Jinjun WANG,Kyung Chun KIM,*

a Fluid Mechanics Key Laboratory of Education Ministry, Beihang University, Beijing 100083, China

b School of Mechanical Engineering, Pusan National University, Busan 46241, Republic of Korea

KEYWORDS

DDES;

Dynamic stall;

Pitching airfoil;

PIV;

Transitional Reynolds number

Abstract This research examines the vortex behaviors and aerodynamic forces in dynamic stall phenomena at a transitional Reynolds number (Re=90000) using experimental and numerical approaches. Periodic sinusoidal pitching motion at two different reduced frequencies is used to achieve the dynamic stall of a NACA 0012 airfoil. Several leading edge vortices form and detach in the dynamic stall stage. The flow then quickly transitions to a full separation zone in the stall stage when the angle of attack starts to decrease. There is discrepancy between the phaseaveraged and instantaneous flow field in that the small flow structures increased with angle of attack, which is a characteristic of the flow field at the transitional Reynolds number. The interaction between the streamwise vortices in the three-dimensional numerical results and the leading edge vortex are the main contribution to the turbulent flow.In addition,the leading edge vortex that supplies vortex lift is more stable at higher reduced frequency,which decreases the lift fluctuation in the dynamic stall stage. The leading edge vortex at higher reduced frequency is strong enough to stabilize the flow, even when the airfoil is in the down-stroke phase.

1. Introduction

The blades of a horizontal-axis wind turbine need to change pitch angle all the time to work efficiently in the case of unsteady incoming flow. However, this motion causes strong unsteady aerodynamic load on the blades. Dynamic stall happens during the motion of blades which is the key reason for the unsteady aerodynamic load.1One of the main characteristics of dynamic stall is that the maximum lift of an airfoil undergoing unsteady motion is far beyond the maximum lift that the static airfoil can reach. Other characteristics of dynamic stall include the formation and shedding of vortices of different size.2

The aerodynamic characteristics of dynamic stall delay the static stall at high angles of attack, which has attracted many researchers because it can play an important role in wind turbines, aerospace, and energy harvesting. McCroskey3, Carr4,and Ekaterinaris and Platzer5comprehensively reviewed dynamic stall using experimental and numerical techniques.The dynamic stall of a pitching airfoil can be divided into four stages: no stall, stall onset, light stall, and deep stall6. These four stages can also be divided into three stages according to the development of the aerodynamics loads:pre-stall,dynamic stall, and stall.

The pre-stall stage is a combination of no-stall and stall onset since the aerodynamic loads follow quasi-static aerodynamic theory in these two stages. The development of a Leading Edge Vortex (LEV) and large peak force are the main characteristics of the dynamic stall stage. In the stall stage,the aerodynamic loads drop quickly, and the flow transitions to a separation zone, which is similar to static stall. The separation behavior of flow is also divides dynamic stall into light and deep dynamic stall.

In light dynamic stall,the LEV strengthens itself in the upstroke phase and terminates in the beginning of the downstroke phase.7In deep dynamic stall, the LEV transitions to severe flow separation in the early up-stroke phase.8LEV is thought to be the key flow structure in dynamic stall. Thus,understanding the development features of LEV can help explain the aerodynamic characteristics of dynamic stall.

There are many parameters that influence the flow in dynamic stall. The Reynolds number and the reduced frequency were two important non-dimensional parameters to describe the pitching motion of an airfoil.3The reduced frequency is defined as k=πfc/U∞and is introduced to indicate the ratio of the convective time scale and the forced oscillation time scale.Here the f is the motion frequency of airfoil,the c is the chord length of the airfoil and the U∞is the free-stream velocity. The Reynolds number is defined as Re=ρU∞c/μ and is a common parameter in fluid dynamics. Here the ρ is the fluid density and the μ is the free-stream viscosity. The combination of these two parameters leads to complicated rules for vortex evolution and force dynamics.

The Reynolds number is often used as a reference to distinguish different kinds of flow. Aircraft, helicopter rotors, and turbo-machinery often operate at high Reynolds number beyond the order of 106.Small to medium wind turbines work at medium Reynolds numbers on the order of 105. Low Reynolds numbers(Re ～O(104))are the operating range of Micro Air Vehicles (MAVs). With the different phenomena of dynamic stall at different Reynolds numbers,the LEV characteristics also exhibit great differences. Numerous researchers have studied the characteristics of a pitching airfoil at different Reynolds numbers. Some recent representative studies are summarized in Table 19-27.

The Reynolds number used in the research in Table 1 are from 103to 106.These studies indicate that the vortex behavior strongly depends on the Reynolds number. At low Reynolds number,the LEV structure is more concentrated,and the maximum vortex strength is higher.At high Reynolds number,the LEV structure transitions to the full separation zone rapidly.More small-scale flow structures can also be observed during the motion process because it is much easier for the vortex structures to lose stability and separate into small threedimensional vortex structures.

Table 1 Non-dimensional parameters of pitching airfoils in previous studies.

The flow field shows more complicated flow structures at transitional Reynolds numbers, which are around 1.0×105.Studying a flow field that mixes the characteristics of these two regimes at transitional Reynolds numbers is important to understand the development of the flow field and aerodynamic forces at different Reynolds numbers. In addition,investigation of the evolution of flow structures, particularly three-dimensional ones, helps in understanding the development of aerodynamic forces during pitching motion since it is closely related to the vortex structure. However, threedimensional approaches are rarely used, including 3D Particle Image Velocimetry (3D-PIV) and 3D Computational Fluid Dynamics(3D-CFD),although there are some 3D CFD works at a low Reynolds number of 2×104.15,16Although there are many 2D-PIV studies at low Reynolds numbers, there are few comprehensive PIV studies at higher Reynolds numbers due to the difficulty of measurement.23-25

Thus, this study mainly focuses on the evolutions of threedimensional flow structures and their influences on the aerodynamic forces during pitching motion at a transitional Reynolds number. The Reynolds number is fixed at 9×104, and two typical reduced frequencies are chosen as parameters. Both 2D time-resolved PIV and 3D CFD approaches are applied to reveal the physics of dynamic stall for a pitching NACA0012 airfoil.

2. Experimental and numerical methods

2.1. Experimental method

An experiment was conducted in a recirculation water tunnel at Beijing University of Aeronautics and Astronautics. The size of the test section was 1000 mm×1200 mm in the spanwise and vertical directions, and the free-stream turbulence intensity was less than 0.8%. A schematic of the experimental setup is shown in Fig. 1. The experimental model was a NACA0012 airfoil with a chord length of c=300 mm and spanwise length of 800 mm. The distance between the top of the airfoil and the water surface was 2 mm, so the effective aspect ratio was extended to 5.33.14The airfoil was manufactured using rigid plastic to reduce the weight and black spray paint to reduce the surface reflection under laser illumination.The model was mounted vertically in the test section and maintained perpendicular to the flow direction, as shown in Fig. 1(a).The distance between the pivot point and the leading edge was one-quarter of the chord length, which follows most of previous studies about dynamic stall. It has been found that moving the pivot point forward is beneficial for the formation of the leading-edge vortex.28,29Thus, this study will not concern the effect of the pivot point.

Airfoil pitching motion was produced by a servo motor(YASKAWA SGM7J) and a Panasonic AFPXHC60T PLC controller. A schematic of the pitching airfoil is shown in Fig. 1(b). The airfoil oscillated around the pivot point in the x-y plane. Since the rotation velocity was much smaller than the free-stream velocity,the effective angle of attack was equal to the angle between the free-stream velocity and chord-line.Given a sinusoidal oscillation as an input, the effective angle of attack α for pure pitching motion can be represented as follows:

The mean effective angle of attack α0and the pitch oscillation amplitude αmwere fixed at 10° and 15°, respectively. The free-stream velocity was fixed at U∞=300 mm/s,and the corresponding Reynolds number was 9×104. The motion frequency was f=0.0318, which corresponds to k=0.1. Thus,the deflection is negligible at the half span location where the velocity fields were measured.

The velocity field was measured by a time-resolved 2D PIV technique.A dual-head ND:YAG laser with 500 mJ/pulse was used to generate a light sheet with a thickness of 1.5 mm.Hollow glass beads with a median diameter of 20 μm and density of 1.05 g/cm3were used as tracer particles. To ensure the spatial resolution in a large field of view,two double-exposure 12-bit cameras (IMPERX B2520) with a resolution of 2058×2456 pixels and 50-mm Nikon lenses were installed in the stream direction. The field of view of one camera was approximately 178 mm×148 mm in the stream direction and vertical direction, respectively. The sampling frequency was 5 Hz, which corresponds to 155 snapshots in one cycle.

Fig. 1 Schematic diagram of experimental setup and pitching airfoil.

The PIV images were analyzed using the Multi-pass Iterative Lucas-Kanade (MILK) algorithm.30The convergent velocities were obtained by a pyramid of 4 and iterations of 7. The size of the interrogation windows was set to 32×32 pixels with 75% overlap. The window’s spatial resolution was 0.78% of the chord length. Erroneous velocity vectors were detected and replaced by peak detection, a normalized median test, and local interpolation.31To increase the measurement accuracy in the measurement of near-wall region,background subtraction techniques were used in the raw PIV pictures to get rid of the negative influence of laser sheet heterogeneity in PIV calculation. Meanwhile, the PIV meshes which contained the airfoil model boundary was eliminated.Phase average process was also done to over 5500 recorded velocity fields corresponding to 38 cycles to suppress the random noise in the flow field. The phase of motion cycle was identified depend on the output signal of servo motor and the angle of airfoil which was got by image identification techniques. The zero phase corresponded to the start position of the airfoil.

2.2. Numerical method

For 3D flow simulations,the flow field is solved using Delayed Detached Eddy Simulations (DDES) and the Finite Volume Method(FVM).The flow inside of boundary layer is modeled using the Unsteady Reynolds-Averaged Navier-Stokes(URANS) approach with the Shear Stress Transport (SST)k-ω turbulence model. However, outside of the boundary layer, the flow is resolved by the Large Eddy Simulation(LES) approach. The CFD flow solver package ANSYS Fluent version 16.1 (ANSYS Fluent, Academic Research, V16.1 2015)was used for the present study.In the case of spatial discretization, the bounced central differencing and second-order upwind formulations were selected for the momentum and turbulence, respectively. Additionally, a second-order implicit scheme was selected for the temporal discretization, and the time step was set as Δt=15×10-5T for all cases to make sure that the Courant-Friedrichs-Lewy (CFL) number is less than 2. The ‘‘Pressure Implicit with Splitting of Operator”(PISO) algorithm was used for the pressure-velocity coupling.

Fig. 2 Computational domain and detailed mesh topology.

Fig. 2 shows the 3D computational domain, which was designed with C-mesh topology. The mesh structure is magnified in different views.The blade is surrounded by a boundary mesh that is normal to the surface of the airfoil. The mesh is dense and fine enough near the leading and trailing edges to capture the strong shear layer and mixing layer in these regions appropriately. The profile section of the straight blade is a NACA0012 airfoil with a chord length of 0.1 m and aspect ratio of 2.The airfoil is enveloped by a boundary mesh normal to the wall with y+lower than 1, which meets the accuracy requirement of DDES solver. All outer boundaries were kept at about 12c away from the blade to make the blockage effect negligible.20The total number of nodes for the final design was 2.9×106, and 500 nodes were placed along the foil and clustered near the leading and trailing edges.

To design a 3D computational domain for DDES simulations,a 2D domain in an x-y system was designed and run with the same boundary conditions. The boundary layer thickness was then computed for when the flow is still attached to airfoil surface. In the DDES approach, the flow is modeled inside of the boundary layer using URANS,while outside of the boundary layer, the solver switches to the LES approach and solve the flow in the wake region. Therefore, the boundary layer thickness allows us to design a mesh with appropriate cell dimensions to make sure that the flow is solved by the URANS solver inside the boundary layer. Next, the 2D computational domain is extruded uniformly in the z-direction with a spatial step of Δz=0.01c.

For the boundary conditions, constant free stream velocity was applied upstream of the domain, and the upper, lower,and downstream boundaries were set to atmospheric pressure.The blade surface has no-slip conditions, and the side boundaries were set to periodic boundary conditions. A reduced frequency of k=0.1, Reynolds number of 1.35×105, and effective angle of attack of α=10°+15°sin(2πft) were chosen to verify CFD solver. Reduced frequencies of 0.1 and 0.2, a Reynolds number of 9×104, and the same effective angle of attack were used later in the study.

2.3. Validation of CFD method

Different computational domains were considered to validate the computational method.Four computational domains with different characteristics are provided in Table 2.Nzis the number of nodes in the spanwise direction. The number of nodes on the airfoil’s surface and the total number of nodes in the whole domain are also provided. In the case of H1, H2, and H3, the number of nodes in the spanwise direction was Nz=160,which was increased to Nz=200 for H4.In the case of the coarse grid(H1),the number of nodes on the surface of the airfoil was Nwall=200, while for the rest of the cases,Nwall=250. Eventually, H3 was chosen as an appropriate computational domain based on the average error computed for each computational domain with reference to H4. As shown in Table 2, the average error for H1 is very high(0.176), while the values for H2 and H3 are 0.0302 and 0.0196, respectively.

The numerical results of lift and drag coefficients were compared with experimental results.21The lift and drag were normalized by chord length,fluid density and free-stream velocity.The experimental parameters are described above.All aerodynamic loads were computed based on integration over the entire surface of the airfoil. Fig. 3 which shows the development of lift and drag coefficients with pitching angle of attack is provided to investigate the accuracy of the numerical solver.As shown in Fig. 3(a), the lift coefficient increases in the prestall region with increasing angle of attack, and the numerical results are in good agreement with the experimental results of Lee and Gerontakos.21In the down-stroke phase, there are greater discrepancies between the experimental and numerical results due to the complexity of the flow in the post-stall region.

Table 2 Comparison of different computational domains with specific characteristics.

Fig. 3 Comparison of lift and drag coefficients for present numerical solver and experimental results (Lee and Gerontakos21) at Re=1.35×105, k=0.1, and α=10°+15°sin(2πft).

In Fig. 3(b), the drag coefficient from the simulation is in good agreement with the experimental results. As the angle of attack increases, the numerical results follow the trend of the experimental results.The discrepancies between the numerical and experimental results might be due to the measurement methods since post processing of the pressure tap results rather than direct measurement was used in experiment. Additionally, the complex mechanism of the flow separation and the development of vortices make the numerical results more unstable in the post-stall region,which is still being considered by other researchers as well.32-34Overall, the numerical method is reliable, although experimental results are still needed as a reference.

3. Results and discussion

3.1. 2D PIV results

Fig. 4 shows the phase-averaged spanwise vorticity (ωzc/U∞)field of the PIV results. The experimental measurement results have been ensemble-averaged over 38 cycles.In the early stage of the up-stroke phase,the flow remains attached to the airfoil.When the angle of attack increases to 15.5°,a vorticity concentration zone is observed at the leading edge of the airfoil,which means that the LEV forms and continually gains vorticity from the leading edge shear layer.With the development of the LEV, a weak vortex with an opposite sign forms between the shear layer and the LEV when the angle of attack increases to 21.67°. When the angle of attack increases to 22.73°, which is nearly the maximum angle, the LEV detaches from the airfoil surface, and a new LEV is formed.

When the airfoil is in the down-stroke phase, the flow quickly transitions to a full separation zone, which is compressed with increases of the angle of attack. The detachment of the LEV is different from the phenomenon observed in experimental results at a lower Reynolds number from Gharali and Johnson18and Mackowski and Williamson14that the LEV detaches from the airfoil until the LEV reaches the trailing edge of the airfoil. In addition, the LEV in the phaseaveraged flow field is more stable than the experimental results at a higher Reynolds number from Taylor and Amitay23and Zanotti et al.25

At high Reynolds number, the flow field is highly random.The phase-averaging process erases some of the flow features.Fig. 5 shows the instantaneous spanwise vorticity field at α=18.57° and 22.73° and the corresponding phase-averaged results to explore the instantaneous flow features. At low angles of attack up to α=18.57°, the phase-averaged fields are similar to the instantaneous fields. However, the discrepancy increases with the angle of attack. At high angles of attack around 22.73°, the main vortex structure of the phaseaveraged field is the same as the instantaneous field.However,small-scale structures form and shed during the pitching motion. These structures are not phase-locked since they are filtered out in the phase-averaging process.

The reason for these differences is probably that there are three-dimensional structures produced by instability at high angles of attack. They interact with the LEV and generate the small-scale structures in the two-dimensional PIV results.Thus,there are different scales of the vortices in the flow field,which is the typical flow feature at transitional and high Reynolds numbers. The complex mutual process of vortices with different scales enlarge the noises of the flow information captured by the PIV,which further increases the noisy level of the calculated PIV data. Thus, the instantaneous flow fields seem to be disordered. This phenomenon has also been observed at high Reynolds numbers by other researchers,such as Taylor and Amitay23, Mulleners and Raffel24, and Zanotti et al.25

Fig. 4 Phase-averaged spanwise vorticity fields at k=0.1 for PIV results.

Fig. 5 Comparison between the phase-averaged and instantaneous vorticity fields at the same angle of attack.

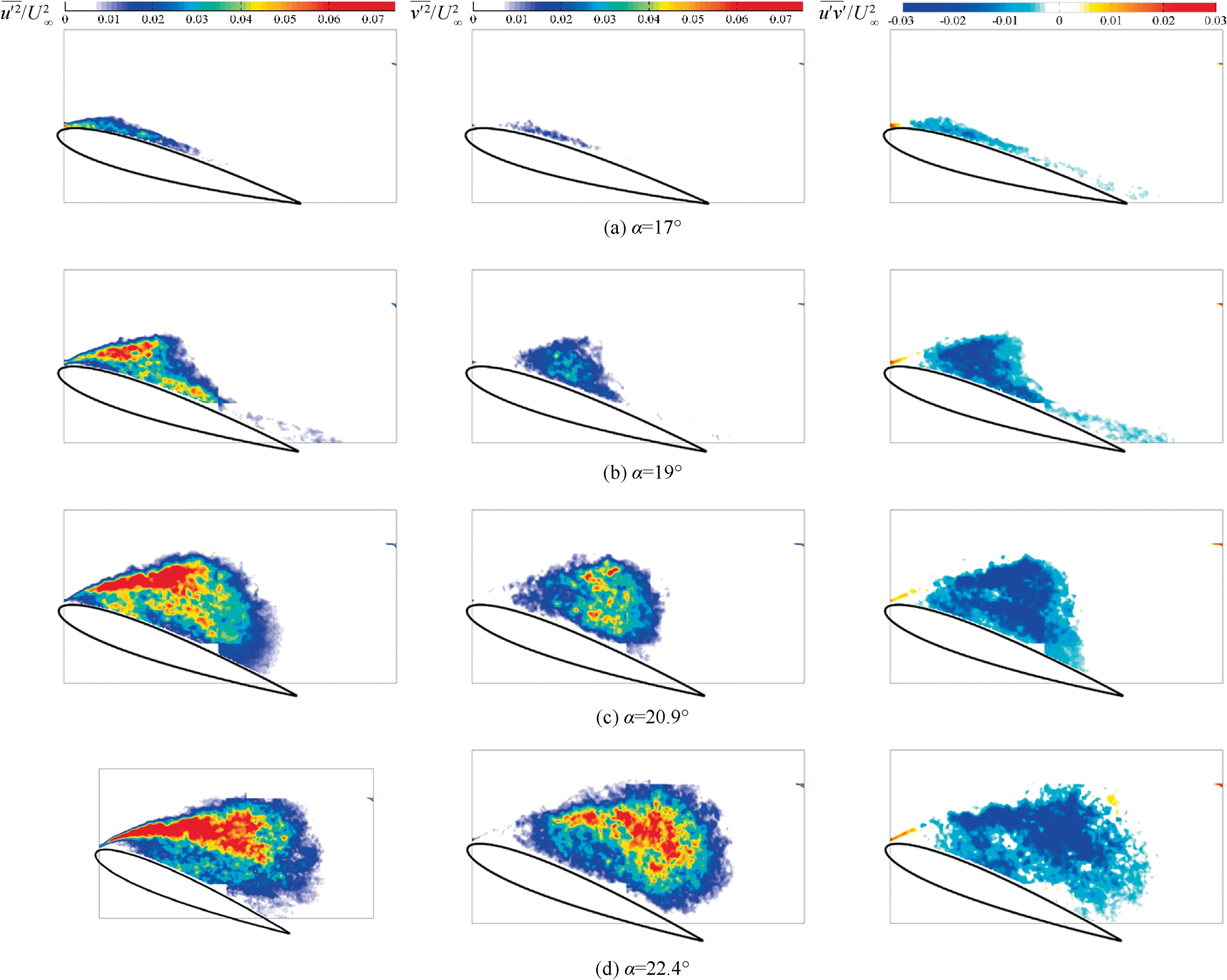
Fig. 6 Normalized turbulence statistics at different angles of attack.

The experimental study of a pitching airfoil indicates that at the chosen transitional Reynolds number, the small-scale flow structures that are filtered by the phase-averaging process contribute substantially to the turbulence at a high angle of attack.To better study these phenomena, a 3D CFD method which performs well in capturing instantaneous small-scale flow structures is used to overcome the shortcomings of filtering such structures by phase-averaged process. Fig. 7 compares the instantaneous flow field between the PIV and CFD results.The CFD results are from the frame at the middle span. At α=19°, the LEV structures show good agreement. When α increases to 20.9°, the LEVs between PIV results and CFD results still show high similarity. However, the differences increase with the angle of attack. The main differences are the vortex strength and the secondary vortex with an opposite sign, as in the case of α=20.9°. When the angle of attack increases to 22.73°,the LEV of the CFD results is more intense than in the PIV results. The signal-to-noise ratio of the CFD results is also lower. The secondary vortex is not clear in the PIV results because the secondary vortex may lose stability and split into small-scale structures that are covered by the noise. Nevertheless, the formation and detachment of the LEV have good agreement between the CFD and experimental results.This proves that the 3D CFD can be used to study the details of the 3D flow field.

3.2. 3D CFD results

Fig.8 shows the spanwise vorticity fields in the mid-span of the airfoil at k=0.1 from the CFD results.In Fig.8(a),the angle of attack is α=19.8°,and the LEV is growing in strength and size.Von Karman streets also shed into the wake near the trailing edge because of trailing edge separation. In Fig. 8(b), the angle of attack is increased to 23.7°. Two LEVs have already detached from the leading-edge shear layer, and the first LEV induces a secondary vortex with the opposite sign beneath the LEV. Additionally, the Trailing Edge Vortex(TEV) begins to develop. One vortex that rotates clockwise can be observed above the TEV. These vortex structures are still stable and move downstream together.

In Fig.8(c),the angle of attack is increased to 24.68°,which is near the maximum angle of attack. One obvious feature of the flow field at this angle of attack is that the flow structures start to lose their stability and deform. The secondary vortex has split into small-scale structures along the airfoil surface.In Fig.8(d),the airfoil just enters the down-stroke phase,and the angle of attack is 24.61°. The original LEV breaks down into complex small structures. Another new TEV is formed and moves the separation zone upward.

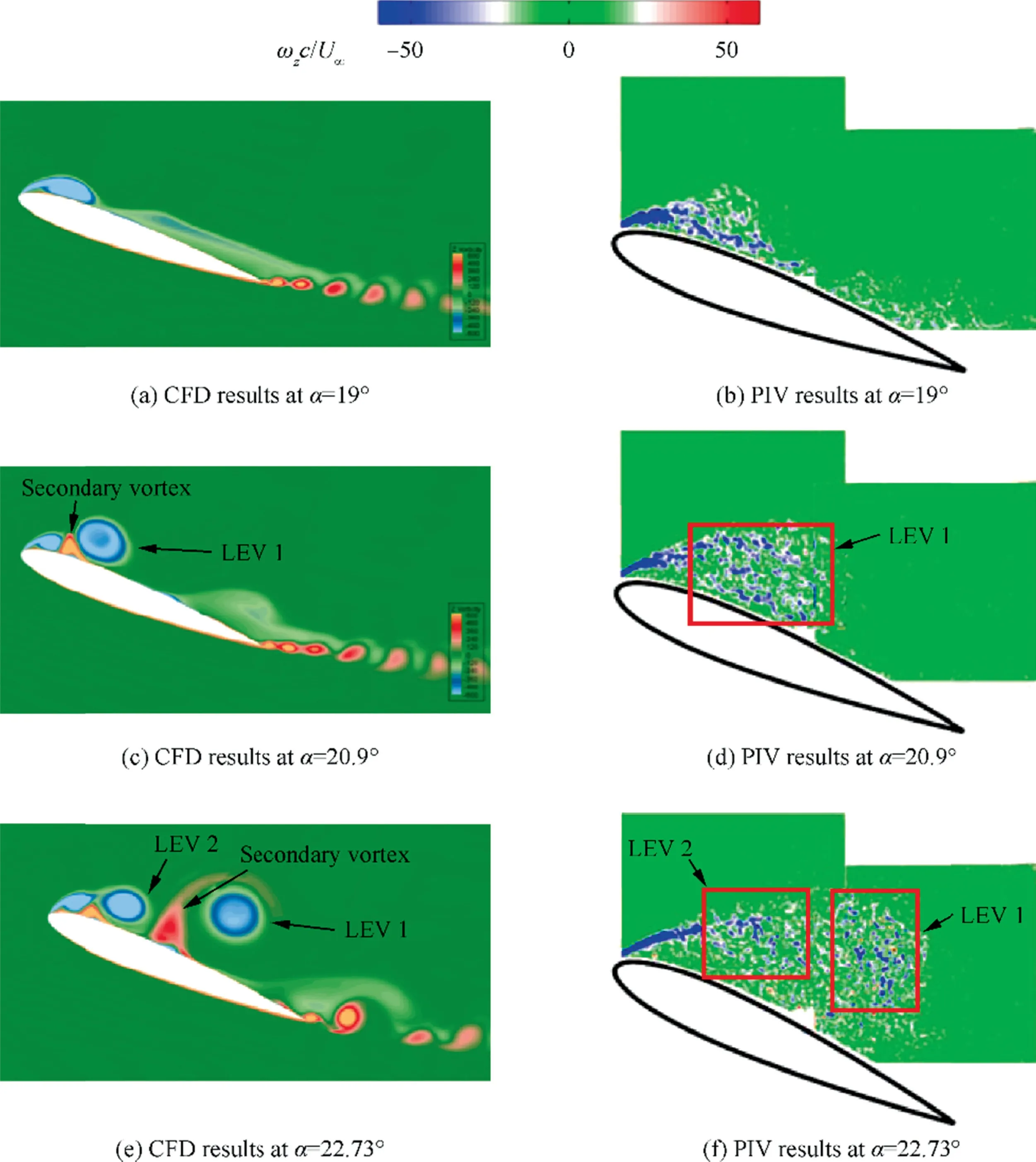
Fig. 7 Comparison between CFD results and PIV results.

Since the flow structures are highly unstable at high angles of attack, it is worthwhile to study the three-dimensional flow field, as shown in Fig. 9.In the three-dimensional case, the Qcriterion isosurface is used as an indicator of turbulent flow structures.Q-criterion is based on the calculation of the second invariant of the velocity gradient tensor.It has been proved as an efficient method to separate the vortex from a shear layer.35Additionally,the isosurface is colored according to the magnitude of the streamwise vorticity to show the strength of the flow structure.In the early stage of the up-stroke phase shown in Fig. 9(a),the LEV extends strictly along the span. With the increase of the angle of attack, numerous LEVs detach from the leading-edge shear layer and move downstream continually, as shown in Fig. 9(b). A cluster of streamwise vortices forms and arrange along the span direction in the rear part of the airfoil.At the same time,the spanwise vortices start losing their stability and have weak three-dimensional deformation.

In Fig.9(c),the angle of attack increases to 24.68°,and the streamwise vortices move downstream and expand. At the same time, some streamwise vortices can also be observed between the first and second LEVs. When the angle of attack reaches the maximum and then decreases to 24.6°, the airfoil enters the deep stall process, and the flow field is completely turbulent.Those streamwise vortices are also observed in other researches to pitching airfoil like Buchner et al.9and Garmann and Visbal36by experimental and numerical simulation methods. However, the Reynolds number they used was on the order of 104which is quite lower than this research. In addition, the motion function they used was pitching at constant velocity not the harmonic function in this research. It states that the streamwise vortices are not special flow structures in this experimental parameters. The reason to its formation may due to the stability of the LEV.

To better study the development of the streamwise vortices,the vorticity field in four y-z frames are shown in Fig.10.These frames are fixed at the present coordinates and do not move with the airfoil.Fig.11 shows the corresponding vorticity field.In Fig. 11(a), the angle of attack is 22.7°, and the streamwise vortices spread over all frames, especially the frame located at 1.25c.These vortices are arranged at the same height in pairs with a mushroom shape in one frame.The width of the vortex pair in one frame is nearly the same.In Fig.11(b),the angle of attack is 24.8°, and the airfoil starts to enter the down-stroke phase.The streamwise vortices keep developing,and the mushroom shape cannot be maintained. The vortices at the same height merge with each other and form a vorticity belt, as shown in the frames located at 0.5c and 1c. However, the streamwise vortices elongate in the vertical direction in the frame located at 0.75c.

Fig. 8 Two-dimensional spanwise vorticity field for the CFD results at k=0.1.

In Fig.11(c)the angle of attack decreases to 24.3°,the flow transitions to turbulence, and distinct vortices cannot be observed. In the development of the streamwise vortices, their characteristics include a spanwise-invariant width, attachment to the LEV, and merging. These substructures are assumed to be formed because of the centrifugal instability of the LEV.In Fig. 11(d), the angle of attack is decreases further, and the wake behind the airfoil shrinks as the vortex strength gradually loses strength. With dynamic stall, the core vortex is strong enough to remain as a coherent structure, while with decreasing of angle of attack,the vortices lose their energy and appear as large eddies, which do not have any order and diminish rapidly.

3.3. Comparison of different k

Fig. 10 Schematic of four chosen y-z frames.

Fig. 11 Streamwise vorticity in four y-z frames for the CFD results.

Fig. 12 shows the vortex development for a pitching airfoil at k=0.2 from the CFD results.In Fig.12(a),the airfoil is in the up-stroke phase, and the angle of attack increases to α=24.37°. In this instant, the LEV has already developed and separates from the airfoil surface. Additionally, the TEV also begins to grow. In Fig. 12(b), the airfoil is in the downstroke phase, and the angle of attack decreases to α=18°.In this instant, the LEV has already separated and sheds into the wake. Additionally, the TEV forms and is ready to leave the airfoil surface. The secondary LEV is still attached to the airfoil, even though the airfoil is in the down-stroke phase.This suggests that the response time of the flow field is slower at high k. With a further decrease of the angle of attack to α=11.9°, the flow mostly separates from the airfoil surface,but no full separation zone is observed on the suction side of the airfoil.

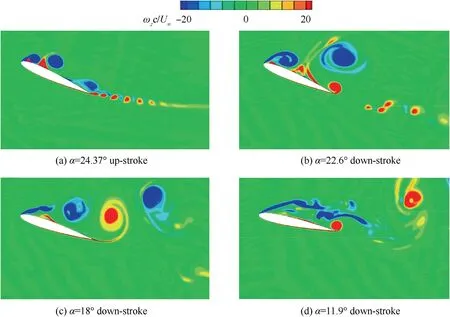
Fig. 12 Two-dimensional streamwise vorticity field for the CFD results at k=0.2.

Fig.13 shows the three-dimensional vortex development at k=0.2. When the angle of attack nearly reaches the maximum, as shown in Fig. 13(a), the LEV has detached from the shear layer. The LEVs and wake streets show good two-dimensional characteristics. In Fig. 13(b), a cluster of streamwise vortices can be observed between the primary and secondary LEVs.The leading-edge shear layer transforms into a streamwise vortex,which cannot be observed in the case of k=0.1.In Fig.13(c),streamwise vortices develop and multiply.At the same time,the TEV formats with streamwise vortices which is formed at the trailing edge of the airfoil and forces the streamwise vortex to separate from the airfoil surface. When the airfoil enters deep stall, the flow field is again full of small structures.

Fig. 13 Q-criterion isosurface of the streamwise vorticity for the CFD results at k=0.2.

There is a big discrepancy in the vortex development between the flow fields at the two reduced frequencies. The LEV detaches from the shear layer later and remains stable for a longer time at higher reduced frequency. Furthermore,three LEVs at most can be observed at k=0.1, while there are only two LEVs at k=0.2.The streamwise vortices remain longer in the case of k=0.2. This shows that the airfoil reaches stall later at higher k,which means the rotation velocity is higher. Besides that, it should be mentioned that the streamwise vortices format after the detachment and three dimensional deformation of the LEV at two different reduced frequencies.It can be assumed that the instability which occurs the deformation of the LEV is the reason to the formation of those streamwise vortices.

Fig. 14 Lift and drag coefficients of the pitching airfoil at k=0.1 and 0.2 obtained by CFD.

Fig. 14 shows the lift and drag coefficients of the pitching airfoil at different reduced frequencies. In Fig. 14(a), the lift coefficient increases linearly with increasing angle of attack in the pre-stall region at both k=0.1 and k=0.2. The lift coefficient at different k increases linearly in the pre-stall region, fluctuates in the dynamic stall region, and rapidly decreases in the stall region. In the pre-stall region, the lift coefficient at k=0.2 is a little bit higher than that at k=0.1. The maximum lift coefficient at different k is the same,while the corresponding angle of attack is different.This means that the airfoil reaches the stall stage later at k=0.2.The lift fluctuation at k=0.1 is also stronger than in the other case.

The angle of attack where the lift coefficient starts to fluctuate is the same as the time when the LEV detaches from the airfoil.Since the LEV at k=0.1 detaches earlier and more LEVs are formed during the pitching motion, the vortex lift that influences the lift coefficient is much stronger. At higher k, the airfoil also reaches stall during the down-stroke stage.This means that the LEV is strong enough to keep the flow relatively attached and stable at higher k. Mackowssi and Williamson14found that the lift agrees well with Theodorsen linear theory37which states the amplitude of angle of attack determines the maximum lift at low k and low Reynolds number.The same maximum lift in both cases prove that this phenomenon also exists in transitional Reynolds number.

Fig. 14(b) shows the drag coefficient hysteresis. In general,the drag coefficient for both reduced frequencies increases with the angle of attack.The wake behind the airfoil and separation of flow over the suction side of the airfoil are the reasons why the drag increases with the angle of attack. At k=0.1, the drag coefficient surpasses that at k=0.2 at high angle of attack. This occurs because the dynamic stall occurs right before the maximum angle of attack,which leads to high drag force on the airfoil. But in the case of k=0.2, the flow is not fully separated, which is why the drag coefficient is relatively low in the up-stroke phase. Once the airfoil starts the downstroke phase,the dynamic stall happens at k=0.2,and at this moment, the drag coefficient remains high,as opposed to that at k=0.1.

4. Conclusions

This research focused on the vortex behavior and aerodynamic force of a NACA0012 airfoil during the dynamic stall stage under two reduced frequencies at a transitional Reynolds number of Re=90000. To better study the flow field and aerodynamic force, the two-dimensional time-resolved PIV technique and three-dimensional CFD were used. The angle of attack varied from -5° to 25° and followed a sinusoidal function.

The flow field of the pitching airfoil at k=0.1 and a transitional Reynolds number was first studied experimentally.The flow is attached to the airfoil in the early up-stroke phase.The LEV then takes shape, which indicates that the airfoil reaches dynamic stall. After the detachment of the LEV, the flow quickly transitions to a full separation zone. When comparing the phase-averaged results and the instantaneous results,there were small flow structures in the flow field with increasing the angle of attack. The results of the turbulent statistics also proves this.To better understand the flow field of the pitching airfoil, three-dimensional DDES was used to study the flow field and aerodynamic force at the same Reynolds number and two reduced frequencies of k=0.1 and k=0.2.

Similar flow development was found in the CFD results.Streamwise vortices were also found in the three-dimensional results.The streamwise vortices were arranged along the spanwise direction.The interaction between the streamwise vortices and the LEV promotes the transition of the flow field to turbulence. When comparing the results between the two reduced frequencies, the flow was more stable and the airfoil reaches the stall stage later at higher reduced frequency.The vortex lift produced by the LEV contributes substantially to the lift in the dynamic stall stage. The formation and detachment of the LEV also cause fluctuation of the lift coefficient in the dynamic stall stage.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Nos. GZ 1280, 11722215 and 11721202). This work was also supported by the National Research Foundation of Korea (NRF) grant with funding from the Korean government (MSIT) (No. 2011-0030013,No. 2018R1A2B2007117).