基于孔隙尺度的多孔骨架对固液相变的影响

2019-12-18张艳勇陈宝明李佳阳张自仕

山东建筑大学学报 2019年6期

张艳勇陈宝明李佳阳张自仕

(山东建筑大学热能工程学院，山东济南250101)

0 引言

相变储能材料具有受热、冷却时发生固态—液态—固态周期性存储和释放能量的特性，已经应用到电池热管理、太阳能发电等众多领域。然而大多数的相变材料由于导热系数及比热容较小等原因，很大程度上影响了其在蓄热和放热过程的速度，因此提高相变蓄能材料的导热系数具有重要的意义。在相变蓄能材料中加入高导热性能的骨架材料，为解决相变材料这一不足提供了有效途径[1]。

近些年，基于孔隙尺度的微观研究由于可以得到多孔介质内部骨架和孔隙之间的详细信息，克服在表征体元 REV(Representative Elementary Volume)尺度下多孔介质内部骨架和孔隙结构之间流动和传热方面的不足，而开始受到广泛关注。Wang等[2]基于孔隙尺度，采用数值方法构建了6个四面体和2个不规则十二面体组成的W-P模型，模拟了开孔泡沫金属在恒温条件下的熔化传热过程，使泡沫金属的孔隙率、导热系数和相变材料的导热系数对复合相变材料的有效导热系数有显著影响，但孔径对其影响不大。成骥[3]对单质石蜡相变材料和泡沫铝/石蜡复合相变材料的蓄热性能进行了实验研究，并对比了不同工况下的相变响应时间、温度分布和蓄热时间，相较于单质石蜡，复合相变材料的相变响应时间更短，温度分布也更为均匀。此外，在7 000、12 000和15 000 W/m2等3种加热工况下，复合相变材料的蓄热时间比单质石蜡分别缩短了35.35%、22.14%、39.90%。 Abishek等[4]通过研究微观形态对金属泡沫石蜡复合材料的影响，发现高孔隙率泡沫金属复合材料有利于提高和控制相变材料的融化速度，可用于热能储存或过程温度控制。王慧儒等[5]采用高清相机和红外热像技术，对组合相变材料融化—凝固循环过程与传热特性开展了可视化实验研究，组合相变材料的应用改善了蓄热腔体各单元相变速率的均匀性，提高了平均相变速率。Jin等[6]采用高速红外热成像技术观测到了熔融过程中典型时刻孔隙间温度场的瞬态演变，得到小孔径的泡沫铜能更好地加速相变材料的融化。杲东彦等[7]和陈振乾等[8]研究了泡沫金属中相变材料的相变熔化过程，在相变材料中填充泡沫金属，能有效改善相变材料的温度分布；泡沫金属孔隙率越小，石蜡熔化越快。杲东彦等[9-10]基于孔隙尺度分析了无量纲Ra数、孔隙率及孔密度等参数对融化相变传热过程的影响，发现相变材料的融化率随着Ra数的增大、泡沫金属孔隙率的减少及其孔密度的增大而增大。宋林泉等[11]基于孔隙尺度采用四参数法生成了多孔介质骨架，研究了其物性参数对固液相变过程以及糊状区的影响。姚元鹏等[12]通过构建泡沫金属内固液相变传热模型，对方腔蓄热单元中泡沫铜强化石蜡相变蓄热特性进行了数值分析，泡沫铜可以显著改善石蜡相变的空间均匀性，减小了蓄热区温度梯度，使蓄热速率和火用效率得到了有效提高。

由于多孔介质内部结构的复杂性以及固液相变过程中糊状区内流动和换热高度非线性的特点，传统的数值计算方法在计算有关多孔介质内相变传热时往往会遇到边界复杂、并行计算效率低的问题，而格子玻尔兹曼方法正好解决了传统数值模拟在处理多孔介质内固液相变中遇到的问题。He等[13]对格子玻尔兹曼方法在多孔介质中单相和固液相变传热研究中的应用进行了详尽的综述，认为格子玻尔兹曼方法将在多孔介质固液相变传热的研究中发挥越来越重要的作用。对于纯液相材料的固液相变过程，大量研究已经表明，固液共存的糊状区对相变融化传热有很大的影响[14-15]，但固体骨架的存在对含固液相变过程糊状区的演化和发展缺乏进一步的研究。文章采用描述糊状区流动特征的多孔介质—多相流复合模型[16-17]，重点分析了无量纲瑞利数(Ra数)、普朗特数(Pr数)、斯蒂芬数(Ste数)对多孔介质内相变材料融化过程以及流动换热的变化规律。

1 物理模型和数学模型的建立

1.1 物理模型的建立

物理模型如图1所示，方腔尺寸高×宽=H×H，腔体内部随机分布着四参数法生成的骨架，孔隙率为0.9，图中白色部分表示固体骨架，蓝色部分表示相变材料。相变材料的相变中心无量纲温度为0.2，相变无量纲温度半径为0.1，多孔介质骨架方腔上下壁面绝热，左壁面为高温壁面，其无量纲温度Th为1；右壁面为低温壁面，其无量纲温度Tc为0，而初始无量纲温度T0为0。

图1 方腔内多孔介质骨架模型示意图

1.2 数学模型的建立

1.2.1 控制方程

基于两区域模型，对糊状区中高含液率区(r＞rtr)看作固—液两相流，并将固—液两相流看为不同组分混合的单相物质，将原来适用纯流体的宏观输运方程直接用于固—液两相流区域，而涉及的相关物性参数采用表征参数。低含液率区域(r＜rtr)采用适用范围更广的Brinkmann-Forchheimer-Darcy多孔介质渗流模型，其中渗透率、形态系数由液相率得到，从而建立更加准确的数学模型，在模型中高、低含液率的分界点rtr=0.7[16]。

数学模型中进行了简化假设:(1)流体不可压缩；(2)方腔内液相相变材料的流动为层流；(3)多孔基质和固体相变材料是刚性的；(4)固体和液相中的密度变化通过Boussinesq项进行近似；(5)相变过程中相变材料的体积变化忽略不计。

孔隙尺度下含糊状区的固液相变的控制方程由式(1)～(3)表示为

式中:u为渗流速度，m/s；t为时间，s；r为液相率(对应于多孔介质孔隙率)，其中r=0为固相区、r=1为液相区、0＜r＜1为糊状区；下标fl和fs分别表示相变材料液相和固相；ρ为相变材料密度，kg/m3；cp为相变材料的热熔，J/K；p为相对压力，Pa；υe为有效运动黏性系数，m2/s；T为温度，K；Ktotal为有效导热系数，W/(m·K)；La为相变潜热，J/g；F为外力源项，N。

固体骨架能量方程由式(4)表示为

式中:下标s为多孔介质骨架；ks为骨架导热系数，W/(m·K)。

F为外力源项，由式(5)表示为

式中:υfl为液相流体的动力黏性系数，m2/s；K为多孔介质的渗透率，md；结构函数Fε为多孔介质的形状因子；g为重力加速度，m/s2；β为热膨胀系数，1/K；Tref为参考温度，K。

在糊状区的低含液率区域(r＜rtr)，对应的渗透率K、有效导热系数ktotal分别由式(6)和(7)表示为

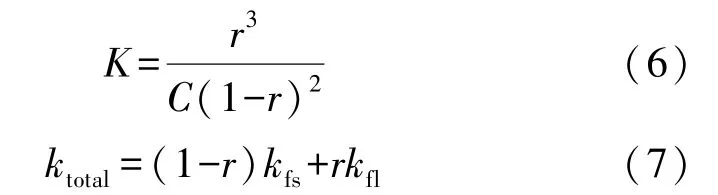
式中:C为糊状区常数；在纯流体区，r=1，式(1)～(3)转化为纯相变材料固液相变的控制方程；在固相区，r=0，式(1)～(3)转化为导热的控制方程；在糊状区的低液相率区域，0＜r＜rtr，可看作多孔介质区域，该区域内流动、传热满足式(1)～(3)；在高液相率区域，1＞r＞rtr，液固两相流的表征导热系数ktotal、表征运动黏度Ve由式(8)和(9)[18]表示为

式中:ϕ为相变材料固相体积分数，即ϕ=1-r。

相变材料的液相分数由焓法求解，由式(10)[19]表示为

相变材料的焓值En和温度Tfl之间的关系由式(11)表示为

式中:Ens和Enl分别为相变开始时相应温度Tfs的焓值和相变完成时对应温度Tfl相应的焓值，J/kg；TR为相变半径，TR=(Tfl-Tfs)/2，K。

根据相变材料的液相率，r由式(12)表示为

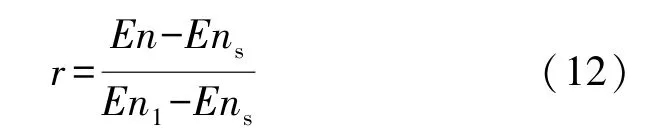
由式(10)～(12)可知，固体骨架传热的纯导热方程(4)中的温度场与液相分数是相互耦合的，可以通过数值迭代求解。为减少控制方程中的变量，探讨相变过程中糊状区对相变过程影响的机理，引入的无量纲参数如

其中，αfl为相变材料的热扩散率，m2/s；σ为有效热熔比；R为有效导热系数比；Da为达西数。把上述无量纲参数带入到式(1)～(4)中，得到对应的无量纲控制方程分别由式(13)～(16)表示为

式中:σtotal为有效热熔比；Rs为有效导热系数比。

1.2.2 相变格子玻尔兹曼

求解用双分布格子玻尔兹曼方法 D2Q9模型，模型对应的速度和温度演化方程及平衡态方程由式(17)～(20)[20]表示为

式中:fi(x，t)、gi(x，t)为t时刻x位置的微粒在i方向上的分布函数，简写成fi、gi；δt为格子时间步长；wi为权系数；ei为i方向上的格子速度；cs为格子声速。

对应源项Fi、Sri分别由式(21)和(22)表示为

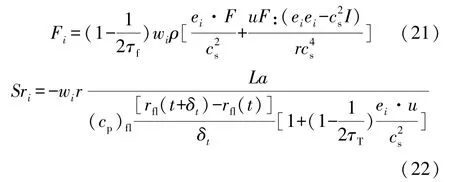
速度与温度演化方程中的无量纲松弛因子τf、τT分别由式(23)和(24)表示为

宏观密度、速度和温度由式(19)和(20)求得，由式(25)～(27)表示为

外力源项F中含有流动速度u，通过求解，由式(28)表示为

式中:V为临时速度，由式(29)表示为

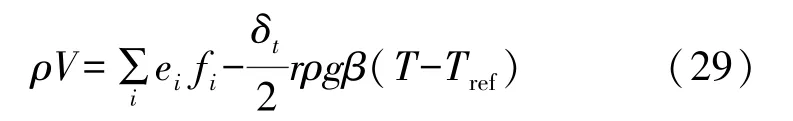
式中:c0、c1分别由式(30)和(31)表示为

使用多尺度Chapman-Enskog方法对演化方程式(17)和(18)展开，可得到对应的宏观方程式(1)～(4)。

2 网格无关化的验证

4种不同网格数，无量纲参数Ra为5.0×105、Pr为1、Ste为5时，高温壁面平均Nu数随无量纲时间Fo数的变化曲线图如图2所示。无量纲Nu数定义由式(32)表示为

图2 4种网格数下高温壁面平均Nu数随无量纲时间Fo的变化图

以最大网格数180×180为基准，比较其他3种网格数下高温壁面平均Nu数的相对误差，网格数分别为80×80、100×100、150×150 时，其相对误差分别为4.328%、3.258%、1.904%。可以看出，随着网格数的增加，相对误差越来越小，当网格数为150×150时，其相对180×180网格数的相对误差仅为1.904%，因此可以认为网格数为150×150时满足精度要求。

3 结果与分析

3.1 Ra数对融化换热的影响

当Ste为 10、Pr为 1，而Ra分别为 104、105、106情况下，固液相变过程中不同时刻的液相率场、流场的分布情况如图3所示。白色代表固体骨架，红色代表液相相变材料，蓝色代表固相相变材料，介于红蓝之间的为糊状区。由图3可知，当Ra数相同时，在相变发生的初期，糊状区基本与上下壁面垂直，因为热量的传递方式主要是导热，随着融化的进行，在自然对流浮升力的作用下，流体先流经方腔上部，然后再流到方腔下部，导致方腔上方得到的热量多于下部，因此产生了糊状区弯曲，且呈现上窄下宽的形状。同时可以看到糊状区边界的不平滑，这主要是由于骨架的不规则性引起的。但当Ra数较小时，糊状区从开始时刻至达到准稳态阶段一直与上下壁面垂直。当Ra数不同时，相同Fo数下Ra数越大，相变材料融化速率越快，且糊状区上窄下宽现象越明显。由分析可知Ra数对多孔介质内固液相变过程有很大的影响。

图3 不同Ra下相场随Fo数变化云图

在不同Ra数下液相率和热壁面平均Nu数随Fo数变化图如图4所示。融化率随着Fo数的增加而增加，直至趋于稳定；热壁面平均Nu数随着Fo数的增加而急剧下降，并缓慢减少直到达到准稳态时趋于稳定。在Fo＜0.05时，相变发生的初期由于热量传递主要通过热传导进行，故不同Ra数下的融化率和高温壁面平均Nu数发生重合，此时Ra数对融化传热影响不大，且热壁面处的温度梯度逐渐减小，导致在初始时刻平均Nu数急剧下降。随着时间的推移，当0.05＜Fo＜0.4时，由于自然对流强度的增强，液相区逐渐增多，融化率逐渐增大，换热的主要方式由热传导逐渐转变为自然对流换热，限制了热壁面平均Nu数的急剧下降，直到达到准稳态阶段(Fo＞0.4)，高温壁面处的Nu数和液相率都达到稳定。对比不同大小的Ra数，由于Ra数越大表示自然对流强度越强，故随着时间的增加，Ra数越大，融化速度越快，且达到准稳态阶段时，融化率和热壁面Nu数都越大。

图4 不同Ra数下液相率Vf/V和热壁面Nuave随Fo数的变化图

3.2 Ste数对融化换热的影响

Ste数表示相变显热与相变潜热的比值。Ste数分别为0.1、1和10时，在Ra为106、Pr为1的情况下，相变材料的液相率随无量纲时间Fo数变化如图5(a)所示。Ste数越大，在同一时刻相变材料的液相率和融化速度都越大。主要是因为Ste数越大，相变材料融化显热越大，潜热就越小，高温壁面传递的热量更多地用于相变材料的温升，而不是作为潜热储存在相变材料中，从而更易达到相变所需要的温度，导致方腔内的自然对流强度增加。

不同Ste数下热壁面平均Nu数随Fo数变化曲线如图5(b)所示。在融化的前期，Fo＜0.02时，热壁面平均Nu数迅速下降；0.02＜Fo＜0.4，Nu数下降缓慢；Fo＞0.4，热壁面Nu数不再发生变化。主要是在前期热量的传递以导热为主，随着时间的推移自然对流传热逐渐增加。对比3种情况下的Nu数变化曲线，Ste数越小，到达准稳态阶段，热壁面平均Nu数就越大。主要是因为Ste数越小，其潜热越大，相变材料融化所需要的热量就越多，左侧热壁面传递的热量不易向低温壁面传递，而是累积下来融化相变材料，故高温壁面温度梯度就会越大，从而热壁面平均Nu数就越大。

图5 不同Ste数下液相率Vf/V和热壁面Nuave随Fo数的变化图

3.3 Pr数对融化换热的影响

在流体流动与传热的研究中，Pr数作为一个无量纲参数来表征流体的动量交换能力和换热能力，反映了流体的物理性质对流体流动与传热过程的影响。为了研究Pr数对多孔介质骨架内固液相变的影响，分别取Pr为0.01、0.1和1，其他参数为Ra为106、Ste为10。液相率和热壁面Nu数随无量纲时间Fo数的变化如图6所示。在Pr分别为0.1和1工况下，当Fo＞0.15时，相变材料的融化率曲线几乎完全重合，在低Pr数下(Pr＜0.1)，随着Pr数的增加，相变材料的融化速度越快，且达到准稳态阶段时，融化率和热壁面Nu越大。Pr数表征流体流动中动量扩散与热量扩散之间的比值，Pr数越大，表征流体流动中动量扩散能力越强，自然对流越强，融化速率越快，达到稳定状态时热壁面平均Nu数越大。