基于RBF 神经网络的绞吸挖泥船施工产量预测研究及分析

王柳艳，陈新华，王伟

（中交疏浚技术装备国家工程研究中心有限公司，上海 201208）

目前，在绝大多数的疏浚工程中，疏浚员能调节的控制变量主要有绞刀转速、桥架下放深度、泥泵转速、横移速度、台车步进距离，这些重要的控制参数主要依靠疏浚员丰富的施工经验来确定。在施工过程中，影响绞吸挖泥船产量的因素众多，考虑到工程项目及作业环境等因素，许多因素很难量化，随机性大且相互影响。鉴于该控制系统是多参数、非线性、大时滞系统，以往基于绞吸挖泥船疏浚作业过程进行的理论研究及物理模型搭建，在控制系统中没有太大的实际应用意义。因此，本文研究将5 个可控操作变量和绞吸挖泥船的瞬时产量看作黑盒问题，利用数据驱动的方法建立绞吸挖泥船产量模型并进行产量预测，该模型可为下一步对绞吸挖泥船优化控制器的实现提供较为精准的产量模型。

1 绞吸挖泥船施工产量RBF 神经网络预测模型设计

1.1 绞吸挖泥船理论模型

绞吸挖泥船的瞬时产量W（m3/h）取决于流量Q（m3/h）和泥浆混合物浓度C（%），表达式通常如下[1]：

式中：r 为排泥管半径；v 为泥浆流速。

在本次施工工况确定的条件下，根据开挖的土质，所需的排距及相应的排高、扬程也基本确定，因此泥泵的流量一般不能提高[2]。由于压力传感器安装在泥泵吸口处，密度计与流量计安装在泥泵管路上，相距较远，采集的数据之间存在一定的时间间隔，因此，式（1）存在大时滞问题。

绞刀破土切削过程中，绞刀切削泥土的体积量随绞刀切削面和横移速度的变化而变化[3]：

式中：Vc为单位时间内绞刀切削泥沙的体积；bc为绞刀切削宽度；dc为绞刀切削深度；vs为横移速度。

泥沙被切削后，随着绞刀旋转与水形成泥浆混合物，绞刀切削下的泥沙粉碎程度与单位时间内切泥厚度和当前土质有关。切削厚度dd的表达式如下[4]：

式中：Zc为绞刀臂数；nc为绞刀转速。

管道内泥浆的体积浓度表达式为：

式中：Vm为单位时间内进入管道的泥沙体积；Dpipe为泥浆输送管道内径，v 为泥浆流速。

在正常疏浚情况下，Vm和单位时间内绞刀切削的泥沙体积按式（5）进行换算：

式中：K 为绞刀挖掘系数，可取0.8~0.9[5]。

通过式（2）~式（4）可知泥浆在管道内形成过程中，绞刀转速、横移速度、步进距离、桥架下放深度、泥泵转速会对泥浆浓度产生影响。但在实际施工过程中，现场作业环境多变，经验系数不可取，控制参数与实际操作下输出量的关系不明确，以上线性表达的绞刀切削系统及管道输送系统的数学模型是无法应用在本次产量控制系统这样的多输入单输出非线性模型中的。因此本文将绞吸挖泥船产量与影响其关键控制因素之间的关系看作黑盒问题，利用数据驱动的方法进行研究。

1.2 RBF 神经网络数据建模

绞吸挖泥船施工产量多输入单输出的RBF 神经网络结构，见图1。

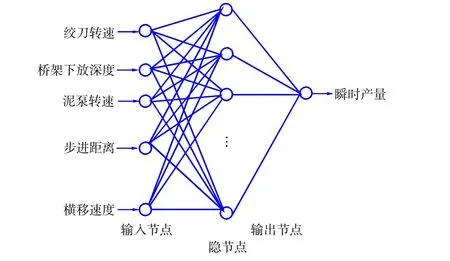
图1 绞吸挖泥船施工产量RBF 神经网络模型Fig.1 RBF neural network model for construction output of cutter suction dredger

RBF 网络结构中，输入和输出向量分别为：

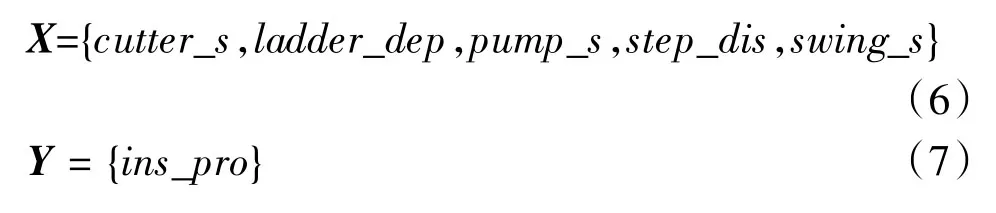
式中：cutter_s 为绞刀转速；ladder_dep 为桥架下放深度；pump_s 为泥泵转速；step_dis 为步进距离；swing_s 为横移速度；ins_pro 为瞬时产量。

1.3 RBF 网络评价指标

决定系数R2表达式如式（8）[6]。

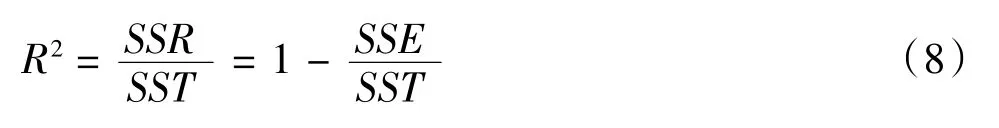
对模型进行线性回归后，评价回归模型系数拟合优度，R2取值在0 到1 之间，R2越大（接近于1），所拟合的回归方程越优[7]。

2 正交实验

为了对绞吸挖泥船的控制变量因素与瞬时产量进行准确建模，满足神经网络算法对数据集特征值的提取更为准确，保证该神经网络具有更好的泛化能力，本次研究采用正交试验法获取绞吸挖泥船的施工数据。

本文所采用的施工数据来自同一艘绞吸式挖泥船，分别在2 个施工地点进行数据采样，这2个施工区域土质具有明显的区别和代表性，如表1 所示。

表1 施工工况土质类型表Table 1 Construction condition soil type

2.1 正交试验数据采集

正交试验设计是研究多因素多水平的一种设计方法，它是根据正交性从全面试验中挑选出部分有代表性的点进行试验[8]。本次正交试验按五因素、四水平进行设计。四水平指根据每个控制变量的可调节安全施工范围分别取4 个水平，即低、中、高、最高。基于以上固定工况，在数据采集过程中，横移速度与绞刀转速是连续变化的，在桥架抬升及下放、台车步进及换桩过程中，数据持续存储，每组试验均采满1 个横移周期。

2.2 数据预处理

1）插值

由于实船数据采集过程中，传感器并非每秒都采集存储数据，只有当信号发生变化时，数据才进行存储，因此每个信号点的数据记录都不是完整的，首先需要对建模输入输出的5 组数据进行插值，本文采用临近点插值法进行信号点插值、补充。

2）滤波

由于绞吸挖泥船上的大部分信号采集装置在信号产生、转换、传输的各个环节中易受供电电源及现场施工条件干扰，导致这些信号点存储的数据中包含噪声和干扰信号，因此，在利用神经网络建模前需要对输入输出数据进行滤波，本次滤波采用中值滤波法。滤波结果见图2、图3。

图2 绞刀转速滤波前后对比图Fig.2 Comparison of cutter speed before and after filtering

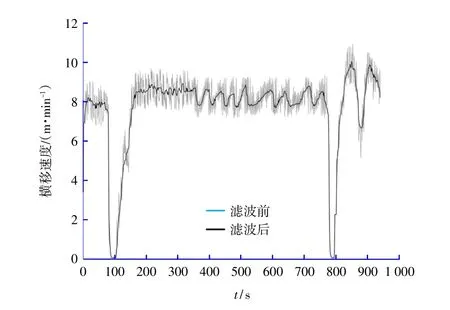
图3 横移速度滤波前后对比图Fig.3 Comparison of swing speed before and after filtering

3）数据切割

在绞吸挖泥船换桩时，瞬时产量都是非常低的值。因此，为了准确地对影响挖泥船产量的控制因素进行影响因子分析，本文将施工数据按1个换桩周期进行切割，删除在换桩时的数据，截取在换桩周期内的挖泥数据进行分析。

3 实验结果与分析

3.1 可控制因素分析

信息增益是特征选择的重要指标，它定义为1 个特征能够为分类系统带来多少信息，带来的信息越多，说明该特征越重要，相应的信息增益也就越大。

本次研究将通过信息增益率对影响产量的控制因素进行影响因子分析，探索施工过程中这些控制因素对产量影响的大小。绞吸挖泥船在施工地点A 与施工地点B 的信息增益率排序情况如表2 所示。

表2 施工地点A 与施工地点B 的控制变量对产量影响的信息增益率Table 2 Information gain rate of control variables on production in working condition A and B

通过计算得到施工地点B 各变量的平均信息增益率为0.716。由表2 的信息增益率可以看出，无论在中粗砂工况下，还是粉砂粉土混合工况下，横移速度的信息增益率都是最大的，在挖泥切削过程中，影响产量的主要控制变量为横移速度。

3.2 产量预测结果

将经过插值、滤波预处理后的数据，对本文所设计的RBF 神经网络进行仿真预测。

1）在施工地点A 的数据采集过程中，绞吸挖泥船进行了上、下两层土质的挖掘，本次试验选取下层土挖掘时间段，该时间段内数据集共计数据样本8 763 个，从中选取前4 382 个样本作为训练集样本，选后4 381 个样本作为测试集样本，对RBF 神经网络预测的瞬时产量进行评价，与测试样本的实际瞬时产量进行对比，预测效果对比如图4 所示。

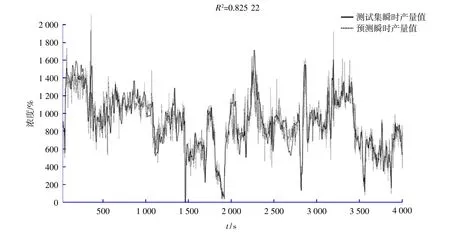
图4 RBF 神经网络测试集A 实际产量与预测产量对比图Fig.4 Comparison of actual output and predicted output of RBF neural network test set A

从图4 可以看出，本次模型训练及预测共耗时约24 s，R2=0.85，从预测结果可以看到该模型不仅预测到测试集样本的变化，且R2=0.85，表明预测精度及拟合效果较好。

2）在施工地点B 的数据采集中，本次试验数据集共计数据样本21 500 个，从中选取前11 000个样本作为训练集样本，选后10 500 个样本作为测试集样本，对RBF 神经网络预测的瞬时产量进行评价，与测试样本的实际瞬时产量进行对比，预测效果对比如图5 所示。

图5 RBF 神经网络测试集B 实际产量与预测产量对比图Fig.5 Comparison of actual output and predicted output of RBF neural network test set B

由于本次训练集测试集样本数较大，训练及预测耗时稍长，约183 s。对比图5 中瞬时产量的实际值与预测值可以发现，预测结果可以较好地跟踪实际产量的变化，且R2=0.85，表明预测精度及拟合效果也较好。

4 结语

针对绞吸挖泥船控制系统中施工产量的预测，本文提出基于RBF 神经网络算法，分别在A、B两种不同工况下，利用正交试验获得的实际施工数据，建立绞吸挖泥船施工产量预测模型，通过对测试样本集的瞬时产量值与预测值进行对比，结果表明采用数据驱动的方式，利用RBF 神经网络算法适用于控制变量因素对产量的模型搭建及预测，且预测效果良好，该预测模型将为下一步的控制器设计提供可靠的数学模型。但在实际应用中船机设备及动力配备对控制因素的限制问题，以及对5 个控制变量相互之间的影响关系亟需进行深入研究。