神经网络分位数在地震保险中的运用

□ 李仁祥

(兰州财经大学统计学院 甘肃 兰州 730020)

引言

由于地震损失数据具有尖峰厚尾的特性，使得传统的均值线性模型不能很好的解释。于是考虑选择使用分位数回归，因为分位数回归不用设定像传统均值模型的正态分布假设以及建立分布的参数。近几年研究提出了函数系数的分位数回归模型，该模型假设模型的回归参数和分位数水平p有某些函数关系，这样可以直接估计出函数关系，避免了分位数回归需要在不同分位数水平下建模的局限性。例如，孟生旺和李云仙通(2019)[1]过分析了传统分数回归和函数系数分位数回归的优缺点，并基于我国地震损失数据讨论的它们的应用和以及计算了在不同条件下的风险度量。但是，影响地震损失的个因素不一定是线性的关系，如果只是使用分位数回归模型讨论可能会有一定的偏差。例如，许启发(2014)[2]使用神经网络分位数的VaR风险测度，解决了VaR风险测度在尾部风险测度的难题。阮素梅和于宁(2015)[3]使用神经网络分位数模型对证券投资收益条件密度函数预测。何耀耀等(2013)[4]使用神经网络分位数模型推测电力系统短期负荷，得到了更精确的结果。

机器学习算法作为一个新的预测模型，在很多的领域获得了一定的效果，尤其在车险损失的预测和车险费率的厘定。例如，孟生旺(2012)[5]首次使用神经网络预测汽车保险的索赔频率，提高了汽车保险索赔频率的预测准确度。孟生旺(2017)[6]把机器学习算法使用在索赔发生概率和累积赔款预测当中,并基于真实的汽车保险损失数据进行实证检验。

本文将对地震损失数据分别建立线性回归模型、线性分位数回归模型和神经网络分位数回归模型，对比3个模型的结果。神经网络模型目前尚未被用到地震损失数据预测当中，所以本研究具有一定的理论意义；并且相关管理人员在进行决策的时候，本研究结果可以提供一些参考，具有一定的意义。

一、分位数回归

(一)模型确立

为了弥补线性回归只能描述解释变量对被解释变量条件均值影响和随机项要均值是0并且同方差的正态分布，Koenker等提出了分位数回归模型。分位数回归模型描述了解释变量对于被解释变量的条件变化影响，以及它的随机项不用具体的分布假设。

给一个分位点τ(0<τ<1),y为被解释变量，x为解释变量，则分位数回归模型为：QT(Y|x)=XTβτ。其中QT(Y|x)被叫做是τ的条件分为数函数。βτ为估计参数。

(二)参数的估计

分位数回归主要有两种参数估计的方法一种是单纯形算法，另一种是内点法。单纯形算法在处理样本量不大并且自变量个数不多时候得出的参数稳定性比较好，但是处理大量数据运算时候速度会明显下降。而内点法适合样本量比较大，自变量不多的数据。比较常用的是单纯形算法，本文就使用单纯形算法进行参数估计。建立非对称损失函数

基于非对称损失函数，可以通过下式得到回归系数的估计量：

二、神经网络分位数

(一)模型确立

神经网络分位数(QRNN)模型是一个非参数的分位数回归模型。本文使用实践中应用最多的单个隐含层前馈神经网络，其神经网络结构为含有m个输入变量(xi，i=1，2，…，m)的输入层，对于本文这些变量是地震指数，含有n个神经单元的隐含层和1个输出层，对于本文输出层输出的数据就是地震损失数据。模型结构建立如下：

(1)建立从输入层到隐含层的连接。

(2)从隐含层到输出层的模型连接结构。

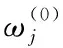
(二)参数估计

本文根据Cannon提出的AIC准则进行最优隐含层节点数的选取。

依据AIC准则，使AIC(τ,n)值最小的n*值为最优隐含层节点个数，即:

确定好隐含层节点个数后，通过优化目标函数来实现参数估计。

三、地震巨灾数据分析

(一)数据来源以及初步分析

从中国地震信息网中获得我国大陆地区每次发生地震灾害的基础数据信息，再综合不同时间不同发生地震灾害事件所在省地震局的地震灾害评估信息，本文收集了1990年到2015年一共278次的地震灾害和经济损失信息(单位：万元)。因为地震造成的当年经济损失受通货膨胀或者经济增长的影响，在进行分析前，本节基于GDP的增长率，把地震造成的经济损失数据调节到了1990年的水平。

通过初步分析得出，直接经济损失最小值是3，最大值是49960678，均值是184189，标准差是2996217。由此可以得出，样本数据具有离散性大，有极端值的情况，直接通过观察散点图来得出地震经济损失与地震损失指数的关系比较困难。为了后续数据的直观展示，本小结对地震直接经济损失数据取对数，但是后续的数据分析还是使用未进行取对数的数据，取完对数之后的地震直接经济损失数据的基本统计量为：最小值是1.244，最大值是17.727，均值是6.509，标准差是2.108696，能够看出对地震直接经济损失数据取完对数之后，数据离散程度得到了一定的降低。

对地震损失数据做Shapiro-Wilk检验，得出p值分别为0.0001539和小于2.2e-16。P值都小于0.05，表明地震损失数据在5%置信水平下拒绝原假设，也就是说地震损失数据不服从正态分布。因此使用线性回归分析不能较好的预测地震损失的规律，所以本文讨论使用分位数回归和神经网络分位数模型对地震损失数据规律进行揭示。

(二)变量的选取

考虑到地震震级和烈度之间有一定相关关系，所以本文先使用主成分分析对震级和烈度做了分析，取其第一主成分作为地震损失指数(d)。分别做了地震震级、地震烈度和地震损失指数对地震损失数据的线性回归，其中地震损失指数得出模型的R方是最大的为0.054，其它两个模型分别是0.044和0.038，也就是说地震指数模型的效果比其它两个模型要好。所以本文接下来将使用由地震震级、地震烈度构成的地震损失指数作为被解释变量。d=0.85*震级+0.85*烈度

(三)结果分析

(1)线性回归模型和分位数回归的结果就比较

表1是关于线性回归模型和分位数回归模型的实证结果比较，分位数回归的分位点分别选取0.15、0.25、0.5、0.75、0.9这5个数。

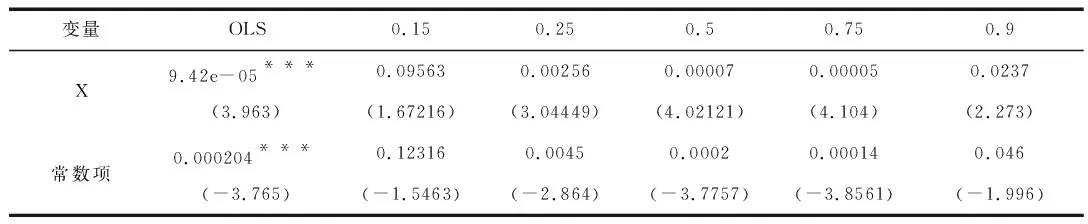
表1 线性回归与分位数回归对比

比较表1中的线性回归模型和分位数回归模型结果可知，线性回归模型和分位数回归模型中的高分位点结果更接近。从表1中分位数回归来看地震损失指数在低分为点和最高分位点影响的显著性没有中间分位点的大，但在线性回归模型中显示有明显的显著影响；从之前的理论可以得知，线性回归模型只能显变量的一个平均变化情况，并不能像分位数回归模型一样能够解释每个分位点的变动情况，因此线性回归模型在解释方面不够精确，应该选择分位数回归模型进行分析结果。

(2)神经网络分位数模型与分位数回归结果比较

根据AIC准则，神经网络隐藏层的节点数选择为5，建立神经网络分位数模型。

通过对均方误差(RMSE)的计算，见表2，发现神经网络分位数模型的预测结果在分位点比较小的情况下表现比分位数回归模型好，精度高。同时在高分位数这块，与神经网络分位数相差不大。出现这样的原因是因为在高分位点附近有很大的地震损失数据，比如唐山大地震和四川汶川大地震这样的数据，造成了在高分位点附近两种模型效果相差不大的情况。但是就表4低分位点附近的数值进一步说明了前面的结论地震损失指数这个变量对地震损失数据的影响表现出非线性关系。所以使用神经网络分位数模型进行结果预测和解释是相对有效的。

表2 神经网络分位数与分位数回归RMSE对比

四、结论

本文先对变量进行一个整合对比，选出最适合的变量进行建模。然后分别使用了线性模型、线性分位数回归模型和神经网络分位数模型构建模型，通过比较发现线性回归模型只有一个结果因为它是对均值回归建模的，所以不能够完全说明变量的分布特征。但是分位数回归模型能够解释各变量在不同分位点的变化、影响程度以及分布情况。又因为变量与解释变量之间存在一定的非线性关系，使用线性回归模型和线性分位数回归模型进行分析就会出现一定的偏差。因此，为了说明变量之间的分布特征，还能获得较好的预测精度，本文选择了神经网络分位数模型进行分析。所以使用神经网络分位数模型进行地震损失数据的预测具有一定的参考价值，并且发现使用该模型在低分位点附近有较好的效果，这为行业相关的管理者提供了一些有用的信息。