例说古典概型中的“等可能”

古典概型在概率研究史上最先被研究，发展较为成熟，它具有以下两个特征：（1）试验的所有可能出现的结果为有限个;（2）每一个试验结果出现的可能性相同。要运用古典概型计算事件A发生的概率，可以借助公式P（A）=[mn]，其中m表示事件A发生可能出现的结果数，n表示所有等可能出现的结果数。

例1 （1）抛掷一枚质地均匀的硬币1次，结果是正面朝上的概率为 ？

（2）同时抛掷两枚质地均匀的硬币1次，结果两枚硬币都是正面朝上的概率是多少？

【分析】（1）抛掷一枚质地均匀的硬币1次，有两种等可能的结果，正面或反面朝上。

（2）在抛掷两枚质地均匀的硬币1次的试验中，同学们很容易误认为出现这三种等可能的结果：两个正面，一个正面一个反面，两个反面。事实上这三种结果的可能性不一样，无论是两个正面还是两个反面，必须满足两枚硬币同时掷出相同的一面，而一个正面一个反面事实上包含两种情况，那就是一正一反和一反一正，在表述上，我们把一正一反和一反一正都统称为一个正面一个反面，由此，一个正面一个反面的可能性大。

在这里，对于一正一反和一反一正的区别，我们借取一元和五角两枚质地均匀的硬币来说明。很显然，一元硬币正面朝上、五角硬币反面朝上和一元硬币反面朝上、五角硬币正面朝上是两种截然不同又等可能的试验结果，所以区分两枚硬币很重要。那么，我们还有其他类似于一元和五角那样区分这两枚质地均匀的硬币的方法吗？同学们自然会想到“起名字”“简称”“缩写”“编码”等，比如用“红1”“红2”标记两个除颜色外都相同的红球，用“Y”“K”标记衣服和裤子……这些方法既起到区分作用又简单易于书写。所以在此题中，我们不妨记这两枚硬币为Y1和Y2，然后画树状图或表格罗列所有的试验结果，并要注意，每一个实验结果必须是等可能的。

【解答】（1）[12];

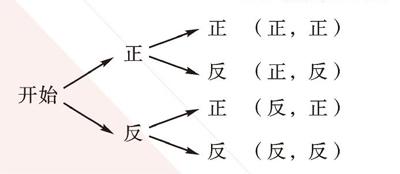
（2）分别记这两枚硬币为Y1、Y2，树状图如下：

[所有可能出现的结果][Y1][Y2]

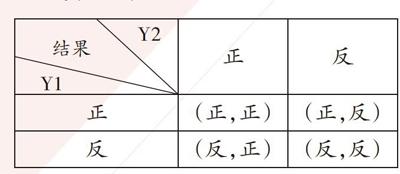
列表如下：

[ 正 反 正 （正，正） （正，反） 反 （反，正） （反，反） ][结果][Y1][Y2]

共有4种等可能的结果，其中，两枚硬币都是正面朝上（记为事件A）的只有1种可能（正，正），所以P（A）=[14]。

变式 抛掷一枚质地均匀的硬币2次，结果两次都正面朝上的概率是多少？

【分析】从“抛掷两枚质地均匀的硬币1次”到“抛掷一枚质地均匀的硬币2次”，这两个实验的结果有什么异同？在这里原来的编号“硬币1”“硬币2”就不再适用了。那么出现几种等可能的结果呢？类似于一个妈妈生了两个孩子，两个孩子都是女儿、两个孩子都是儿子这两种结果与一个孩子是女儿、一个孩子是儿子这一结果可能性一样吗？很显然，不一样！两个女儿是姐妹;两个儿子就是兄弟;一儿一女可能是兄妹，也可能是姐弟，先儿后女是兄妹，先女后儿是姐弟。所以试验中的顺序也很重要，在这里，我们可以用“第一次”“第二次”来区分两次抛掷过程。这个试验中有两个元素，树状图和表格均可罗列所有的结果。

【解答】树状图如下：

列表如下：

[ 正 反 正 （正，正） （正，反） 反 （反，正） （反，反） ][结果][第二次][第一次]

共有4种等可能的结果，其中，两枚硬币都是正面朝上（记为事件A）的只有1种可能（正，正），所以P（A）=[14]。

例2 在4件产品中有2件正品，2件次品。

（1）从中任取出1件产品，该产品为次品的概率为。

（2）若每次取出1件做检查（查完后不再放回），直到2件次品找到为止。求经过2次检查恰好将2件次品找到的概率。

【分析】第（1）题是基础题。第（2）题要特别注意“不放回”，列出的表格从对角线上看非常明显，区别于放回的情况。（B1，B2），（B2，B1）是找到2件次品的情况。题中还有一个陷阱，（A1，A2），（A2，A1）也符合题意哦。聪明的同学们，你们想明白了吗？

【解答】（1）[12];

（2）分别记2件正品为A1、A2，2件次品记为B1、B2，列表如下：

[ A1 A2 B1 B2 A1 （A2，A1） （B1，A1） （B2，A1） A2 （A1，A2） （B1，A2） （B2，A2） B1 （A1，B1） （A2，B1） （B2，B1） B2 （A1，B2） （A2，B2） （B1，B2） ]

共有12種等可能的结果，其中，恰好将2件次品确定（记为事件A）的有（A2，A1）、（A1，A2）、（B2，B1）、（B1，B2），共4种结果，所以P（A）=[412]=[13]。

例3 把3颗算珠放在计数器的3根插棒上构成一个数字，例如，如图摆放的算珠表示数300。现将3颗算珠任意摆放在这3根插棒上。

（1）若构成的数是两位数，则十位数字为1的概率为;

（2）求构成的数是三位数的概率。

【分析】（1）此题很多同学会错解：所有等可能的结果有三种，12、21、30，其中十位数字为1有一种，从而得到错误答案。

（2）此题的错解：所有等可能的结果有10种，3、30、21、12、300、210、201、120、102、111，其中三位数有6种，从而得到错误答案P（三位数）=[610]=[35]。

看到这些错解我们会觉得非常遗憾，更想弄明白究竟错在哪？接下来让我们一起来探个究竟，寻个明白。

在第（1）问的解答中，12、21、30真的是等可能的实验结果吗？细细琢磨，不难发现它们不是等可能的。比如12和30，12表示只要其中任意一颗算珠插在十位的棒上，余下两颗插在个位的棒上;30则表示所有的算珠都要插在十位的棒上，所以，12比30的可能性要大，而12和21具有一定的对称性，其可能性是一样的。既然12、21、30三者的可能性不一样，那么这种摆放方式就不符合古典概型的基本特征，计算得到的概率必然是错误的。由此及彼，再看第（2）问，错误的实质一样，那就是罗列的所有结果不具有等可能性，必然导致模型使用错误。

【解答】（1）[37]。

（2）将3颗算珠任意摆放在3根插棒上，所有可能出现的结果有：（百，百，百）、（百，百，十）、（百，百，个）、（百，十，百）、（百，十，十）、（百，十，个）、（百，个，百）、（百，个，十）、（百，个，个）、（十，百，百）、……、（十、个、个）、（个、百、百）、……、（个，个，个），共有27种，它们出现的可能性相同。所有的结果中，满足“构成的数是三位数”（记为事件A）的结果有19种，所以P（A）=[1927]。

同学们，希望你们能通过阅读此文练就一双慧眼，在古典概型中找到真正所有的“等可能”实验结果。

（作者单位：江苏省常州市新北区吕墅中学）