三数两差经常考 善用概念是妙招
2019-12-17陈新合
陈新合

“数据的集中趋势和离散程度”这一章的主要内容可以概括为:三数两差。三数指平均数、中位数和众数;两差指极差和方差。它们是中考考查的热门知识点,理解概念是解决这类问题的关键。
一、考查三数的概念及意义
例1 (2019·十堰)一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖),则被遮盖的两个数据依次是()。
[组员 甲 乙 丙 丁 戊 平均成绩 众数 得分 81 77 ■ 80 82 80 ■ ]
A.80,80B.81,80
C.80,2D.81,2
【解析】本题考查平均数和众数的概念。平均数是所有数据的和除以数据的个数;众数是一组数据中出现次数最多的数。根据表格数据可先利用平均数的计算公式求出丙的得分:设丙的得分为x,80×5=x+81+77+80+82,求得x=80,所以丙的得分是80分,则这组数据的众数是80,故选A。
例2 (2019·成都)某校开展了主题为“青春·梦想”的艺术作品征集活动,从九年级五个班收集到的作品数量(单位:件)分别为:42,50,45,46,50,则这组数据的中位数是()。
A.42件B.45件
C.46件D.50件
【解析】本题考查中位数的概念。中位数是指:将这列数按从小到大(或从大到小)排列后,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。所以先将数据按照从小到大的顺序排列:42,45,46,50,50,这组数据有5个,则取中间的数据46,故选C。
口诀:排序小大大小,奇取中偶取均。
例3 (2019·长沙)在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛。如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的()。
A.平均数 B.中位数
C.众数 D.方差
【解析】本题考查平均数、中位数、众数和方差的意义。平均数表达一组数据的平均水平;中位数表达一组数据的中等水平;众数表达一组数据出现次数最多的数据;方差表达一组数据的稳定程度。根据题意可知比赛取前5名参加决赛,共有11名选手参加,只要知道自己的成绩和中位数就可以知道是否进入决赛了,所以根据中位数的意义可知选B。
二、考查两差的概念及意义
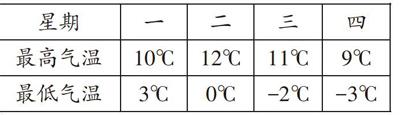
例4 (2019·金华)某地一周前四天每天的最高气温与最低气温如下表,则这四天中温差最大的是()。
[星期 一 二 三 四 最高气温 10℃ 12℃ 11℃ 9℃ 最低气温 3℃ 0℃ -2℃ -3℃ ]
A.星期一 B.星期二
C.星期三 D.星期四
【解析】本題考查极差的概念。极差是一组数据的最大数据与最小数据的差值。温差就是一天的最高温度与最低温度的差值。星期一:10-3=7(℃);星期二:12-0=12(℃);星期三:11-(-2)=13(℃);星期四:9-(-3)=12(℃)。∵7<12<13,∴这四天中温差最大的是星期三。故答案为:C。
例5 (2019·巴中)如果一组数据为4,a,5,3,8,其平均数为a,那么这组数据的方差为。
【解析】本题考查平均数和方差的概念。一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差。求方差的步骤:先平均,再求差,然后平方,最后再平均。计算公式是:s2=[1n][(x1-x)2+(x2-x)2+…+(xn-x)2](简记:方差等于差方的平均数)。由题意得:先根据平均数的概念确定a的值:[4+a+5+3+85]=a,解得:a=5,则这组数据为4,5,5,3,8,其平均数是5,再根据方差公式进行计算:[15][(4-5)2+(5-5)2+(5-5)2+(3-5)2+(8-5)2]=[145],故答案为:[145]。
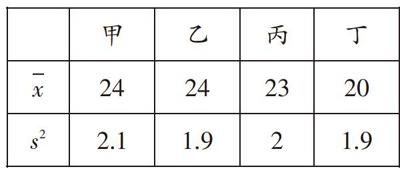
例6 (2019·宁波)去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵,每棵产量的平均数x(单位:千克)及方差s2(单位:千克2)如表所示:
[ 甲 乙 丙 丁 x 24 24 23 20 s2 2.1 1.9 2 1.9 ]
今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植,应选的品种是()。
A.甲B.乙C.丙D.丁
【解析】本题考查平均数和方差的意义。方差是反映一组数据离散程度的量。方差越小,数据的离散程度就越小,稳定性越好。由题意可知:因为甲组、乙组的平均数比丙组、丁组的大,而乙组的方差比甲组的小,所以乙组的产量比甲组的稳定,因此乙组的产量既高又稳定,故选:B。
三、综合考查三数两差
例7 (2019·株洲)若一组数据x,3,1,6,3的中位数和平均数相等,则x的值为()。
A.2B.3C.4D.5
【解析】根据平均数与中位数的概念,分四种情况:x≤1,1 解:当x≤1时,中位数与平均数相等,则得到:[15](x+3+1+6+3)=3,解得x=2(舍去); 当1 当3≤x<6时,中位数与平均数相等,则得到:[15](x+3+1+6+3)=3,解得x=2(舍去); 当x≥6时,中位数与平均数相等,则得到:[15](x+3+1+6+3)=3,解得x=2(舍去)。 所以x的值为2。故选:A。 例8 (2019·滨州)若一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的方差为。 【解析】根据众数的定义先判断出x,y中至少有一个是5,再根据平均数的计算公式求出x+y=11,然后代入方差公式得出答案。 解:∵一组数据4,x,5,y,7,9的众数为5,∴x,y中至少有一个是5,∵一组数据4,x,5,y,7,9的平均数为6,∴[16](4+x+5+y+7+9)=6,∴x+y=11,∴x,y中一个是5,另一个是6,∴这组数据的方差为[16][(4-6)2+(5-6)2+(5-6)2+(6-6)2+(7-6)2+(9-6)2]=[83],故答案为:[83]。 最后,同学们在处理有关“三数两差”的问题时,务必要明确相关概念以及它们的意义,从它们的概念入手分析问题,寻找解决问题的突破口,问题就可以迎刃而解了。 (作者单位:江苏省苏州市阳山实验初级中学校)
