错解总结 能力提升
2019-12-17赵佳佳
赵佳佳
一、概念模糊不清
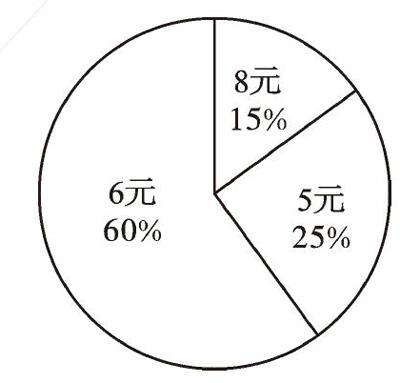
例1 江苏省某校食堂销售三种午餐盒饭的有关数据如图所示,求该食堂销售午餐盒饭的平均价格为。
【错解】6.3元。
【错解原因】用[8+5+63]作为答案,对加权平均数的概念不清楚。这里并不是简单地求三个数据的平均值,应考虑每个数据的重要程度,即所占权重。
【正解】8×15%+5×25%+6×60%=6.05。
二、审题不仔细
例2 求下列一组数据的中位数:2,5,3,4,7。
【错解】3。
【错解原因】审题不清楚,错误地认为一组数据最中间的数据就是该组数据的中位数。
【正解】求一组数据的中位数,应先将数据按大小顺序排列,如果有奇数个数据,取最中间一个,有偶数个数据,取中间两个数据的平均数。因此排序后是2,3,4,5,7,中间数据(中位数)是4。
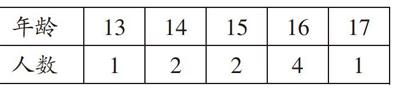
例3 某校对部分参加夏令营的中学生的年龄(单位:岁)进行统计,结果如下表:
[年齡 13 14 15 16 17 人数 1 2 2 4 1 ]
则这些学生年龄的中位数和众数分别是。
【错解】15、4。
【错解原因】没能认清年龄和对应的人数,错误地只取五个年龄的中间值。众数是年龄而不是人数。
【正解】先将数据按顺序排列可得13,14,14,15,15,16,16,16,16,17。共十个数据,中间两个是15和16,中位数则取它们俩的平均数15.5;众数是一组数据中出现次数最多的数据,而不是出现最多的数据的次数,年龄为16的人数最多,因而年龄的众数是16。另外,根据众数的意义,一组数据有时不止有一个众数,也可以没有众数。如数据“5,6,7,6,8,8”的众数是6和8;数据“12,18,46,56,100”没有众数。
三、计算错误,方法不优化
例4 某舞蹈队12名队员身高如下(单位:cm):165,167,169,166,168,164,163,164,165,167,166,162。求她们的平均身高。
【错解】计算错误的各种答案。
【错解原因】计算方法繁琐,基础计算不过关。
【正解】优化方法,简化计算过程,通过观察我们发现,这组数据中的每个数据都较大,并且都接近一个数165,可以用以下方法:将每组数据同时减去165,得到一组新数据0,2,4,1,3,-1,-2,-1,0,2,1,-3。再计算新数据的平均数是[0+2+4+1+3-1-2-1+0+2+1-312]=0.5。所以原数据的平均数是165.5(cm)。
四、跟着感觉走
例5 一组数:1,2,2,3,若再添加一个数据2,则发生变化的统计量是()。
A.平均数B.中位数
C.众数D.方差
【错解】A。
【错解原因】没有通过计算来说明问题,凭直觉,增加一个数平均数就变了。
【正解】通过计算可知原先四个数据的平均数是2,现增加一个数据2,那么现5个数据的平均数依然是2。原先的方差是:[1-22+2-22+2-22+3-224]=[12],
现在的方差是:
[1-22+2-22+2-22+3-22+2-225]
=[25]。故选D。
例6 测试五名学生的“一分钟跳绳”成绩,得到五个各不相同的数据。在统计时,出现一处错误:将最高成绩写得更高了。计算结果不受影响的是()。
A.平均数 B.中位数
C.众数 D.方差
【错解】C或D。
【错解原因】不能很好地理解四个名词的概念。
【正解】个数不变,总和增加,平均数变化;前后都是五个不同的数据,都没有众数;只改变一个数据,平均数变化,方差也发生了变化;五个数据大小排列,最中间第三个数据不变,所以中位数不变。故选B。
五、答题不严谨
例7 (2017·温州)数据1,3,5,12,a,其中整数a是这组数据的中位数,则该组数据的平均数是。
【错解】5。
【错解原因】答题不严谨,排序后片面地认为a只能等于4。
【正解】由题意先将数据大小排列成1,3,a,5,12。由此可知a可以是3,4或者5。由此可求得平均数,一个都不能少。
故答案为:4.8或5或5.2。
六、理解偏差,公式不熟
例8 (2018·南京)某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194。现用一名身高为186cm的队员换下场上192cm的队员,与换人前相比,场上队员的身高()。
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
【错解】B。
【错解原因】不能很好地理解方差的含义。
【正解】关于平均数:个数不变,其中一个数变小,总和变小,平均数也变小。也可通过计算得平均数由188变成187。
方差和平均数息息相关,它集中描述了一组数据中的每个数据偏离平均数的大小,方差越大,越偏离平均数。替换前平均数是188,替换后平均数是187,由此看出替换后的队员身高更靠近平均数,所以方差变小。当然也可以通过计算得方差前后分别是[683]和[593]。故选A。
例9 (2018·张家界)若一组数据a1,a2,a3的平均数是4,方差是3,则数据a1+2,a2+2,a3+2的平均数和方差分别是()。
A.4,3 B.6,3 C.3,4 D.6,5
【错解】D。
【错解原因】想当然地认为每个数据加上相同的数,平均数和方差都应该增加,不能深刻理解平均数和方差的计算过程。
【正解】根据平均数的定义a1+a2+a3=12,那么a1+2,a2+2,a3+2的平均数是:
[a1+2+a2+2+a3+23]
=[a1+a2+a3+63]
=[183]=6,
数据a1+2,a2+2,a3+2的方差是:
[a1+2-62+a2+2-62+a3+2-623]
=[a1-42+a2-42+a3-423]。
这样的计算结果和原数据a1,a2,a3的方差计算公式一致,所以数据a1+2,a2+2,a3+2的方差也是4。这里同学们也可以记住,这种情况下平均数相应增加,而方差不变。
故选:B
同学们,这些错误你都了解了吗?或许你还有不一样的错误,及时整理出来吧。错误并不可怕,只要我们认真总结反思,它将成为我们成功的见证。让我们正确认识错误,消灭错误,一起进步,加油吧。
(作者单位:苏州工业园区青剑湖学校)
