基于0-1整数规划算法的城市地下物流系统网络节点选址

方龙祥，于雪雨

(安徽师范大学 数学与统计学院，安徽 芜湖 241002)

城市地下物流系统是通过城市地下隧道或管道进行固体货物运输的系统，该系统将存储在物流园区、物流基地的货物智能配送到各个终端[1]，“及时配送”是地下物流系统的重要特征。城市地下物流系统具有广阔的发展前景，它的数字化、智能化、自动化、网络化程度较高，可以很好地解决目前物流业制约电子商务发展的问题[2]。构建城市地下物流系统有利于经济的快速增长与环境的可持续发展。从城市地下物流系统网络节点的选址入手构建合肥市地下物流系统，探索一种较为新颖的货物运输方式，从而提高城市物流效率，缓解城市交通拥堵，实现城市的可持续发展。

1 数据来源

地下物流系统还处于理论分析与预测阶段，较难获得精确的数据资料。研究的实证分析部分主要是对合肥市较为拥堵区域(合肥二环及周边区域)的地下物流系统网络进行初步探索，所以物流供需点多选在合肥市二环及周边人流量较大的区域如生产用地、仓储用地、居民区、商业中心等。选中的供需点分布情况如图1所示。为了实证分析的需要提取了各点的经纬度坐标如表1所示。其中，Si(i=1,2,3,…,21)为货物供应点；ei(i=1,2,3,…,21)为货物需求点。

表1 各货物供应点与需求点经纬度坐标

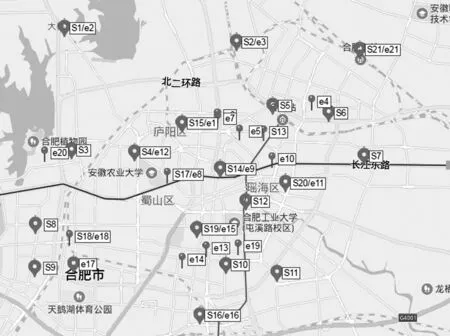
图1 货物供应点与需求点分布

2 数据处理

根据表1中合肥市供应点与需求点的分布经纬度坐标，在地图上进一步测量了供应点与需求点的距离如表2所示。

由以往研究可知，地下物流系统网络节点的服务半径为3～5 km,这里假定节点的服务范围为3 km[3]。结合表2得到各货物供应点到需求点的可达矩阵如表3所示。令可达矩阵为Aij=aij，其中，aij=1或aij=0表示第j列供应点覆盖了第i行需求点或者第j列供应点没有覆盖第i行需求点。

3 问题描述

研究是在已知一组货物需求点与货物供应点的情况下，要求从上述供应点中选择一组货物供应点为所有需求点提供服务，且为了节省前期的建设成本，选中的这组货物供应点的数量要尽可能的少，这是典型的集合覆盖问题[4]。

4 模型构建

集合覆盖模型是一种典型的组合优化模型，它要求用最少的网络节点将所有需求点全覆盖[5]。当问题的规模较小时求解这类问题可以使用0-1整数线性规划的方法。

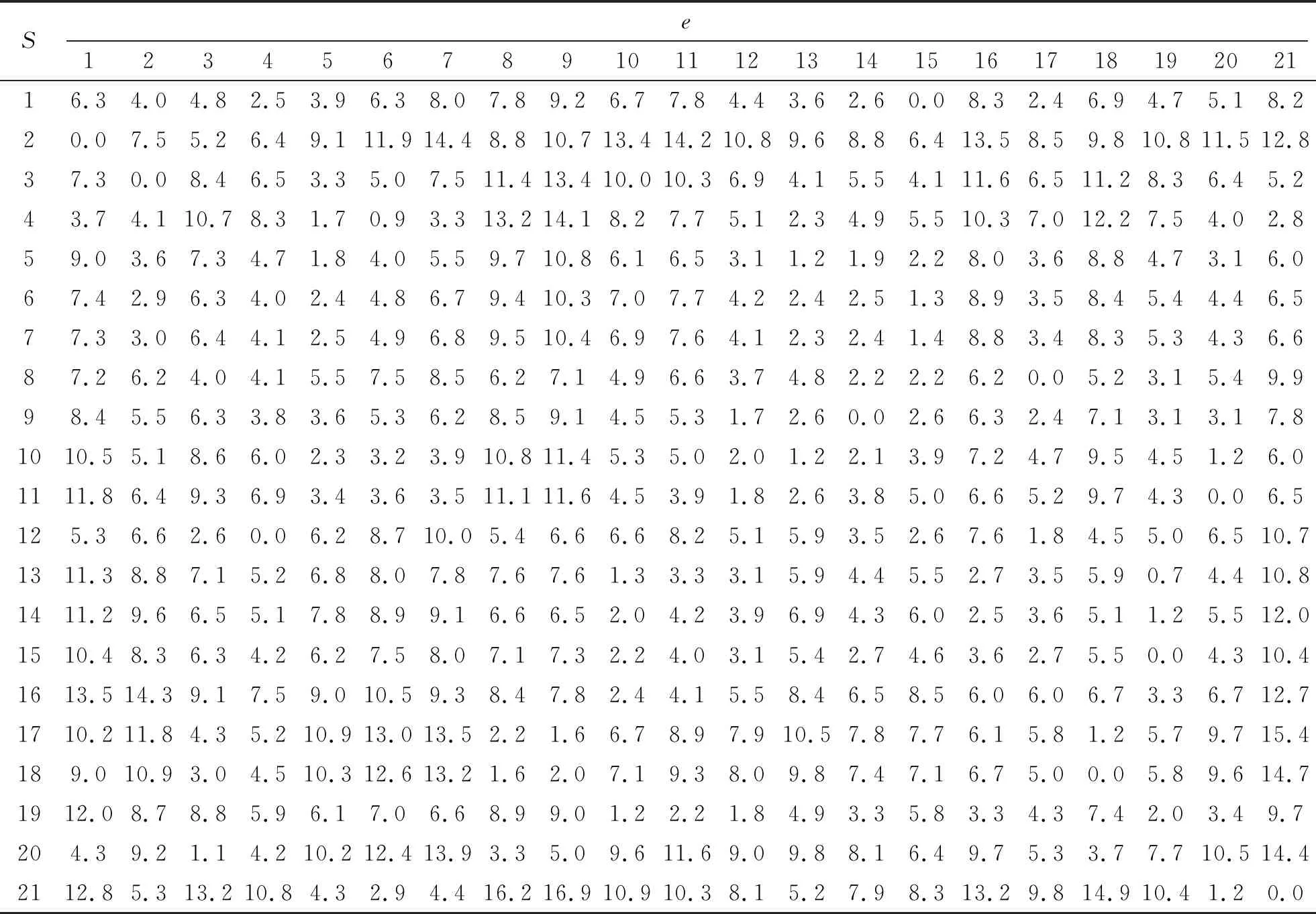
表2 货物供应点与需求点的距离

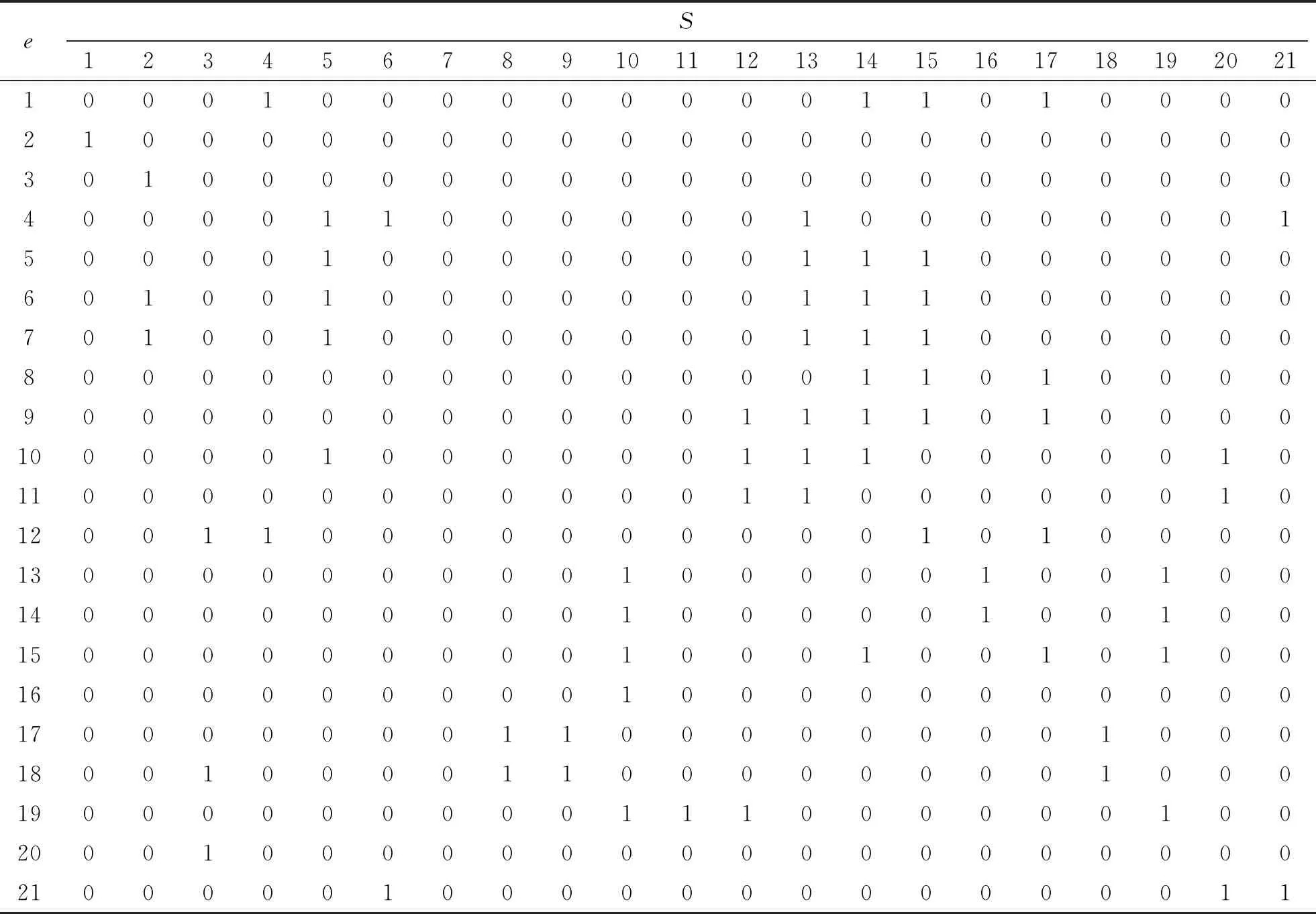
表3 供应点到需求点的可达矩阵

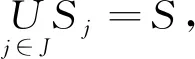
xj=0,1；J=1,2,…,m

为了便于讨论，放松IP变量的整数性要求，得到了它的松弛线性规划问题，令LP代表此规划问题的模型[7]：

xj=0,1；J=1,2,…,m

显然，由IP和LP之间的松弛关系可知，OPTLP≤OPTIP、其中OPTLP、OPTIP分别为LP、IP的最优值。

再由线性规划的对偶理论可知LP的对偶问题，这里将其设为DP：

yi=0,i=1,2,…,n

5 模型求解

由于数据量较少所以采用较为精确的模型求解算法即0-1整数规划算法。同样根据表3供应点到需求点的可达矩阵，找到给每一个需求点提供服务的所有候选的货物供应点集合，如表4所示。

研究0-1整数规划算法的实现使用了LINGO软件。LINGO软件是常见求解线性规划问题的软件，下面是使用LINGO软件实现此算法的主要程序代码，运行结果如表5所示。

min=x1+x2+x3+x4+x5+x6+x7+x8+x9+

x10+x11+x12+x13+x14+x15+

x16+x17+x18+x19+x20+x21;

x4+x14+x17>=1;

x1>=1;

x2>=1;

x5+x6+x13>=1;

x5+x13+x14+x15>=1;

x2+x5+x13+x14+x15>=1;

x14+x15+x17>=1;

x12+x13+x14+x15+x17>=1;

x5+x12+x13+x14+x20>=1;

x12+x13+x20>=1;

x3+x7+x15+x17>=1;

x10+x16+x19>=1;

x10+x14+x17+x19>=1;

x10>=1;

x8+x9+x18>=1;

x3+x8+x9+x18>=1;

x10+x11+x12+x19>=1;

x3>=1;

x6+x21>=1;

@bin(x1);

@bin(x2);

@bin(x3);

@bin(x4);

@bin(x5);

@bin(x6);

@bin(x7);

@bin(x8);

@bin(x9);

@bin(x10);

@bin(x11);

@bin(x12);

@bin(x13);

@bin(x14);

@bin(x15);

@bin(x16);

@bin(x17);

@bin(x18);

@bin(x19);

@bin(x20);

@bin(x21);

End

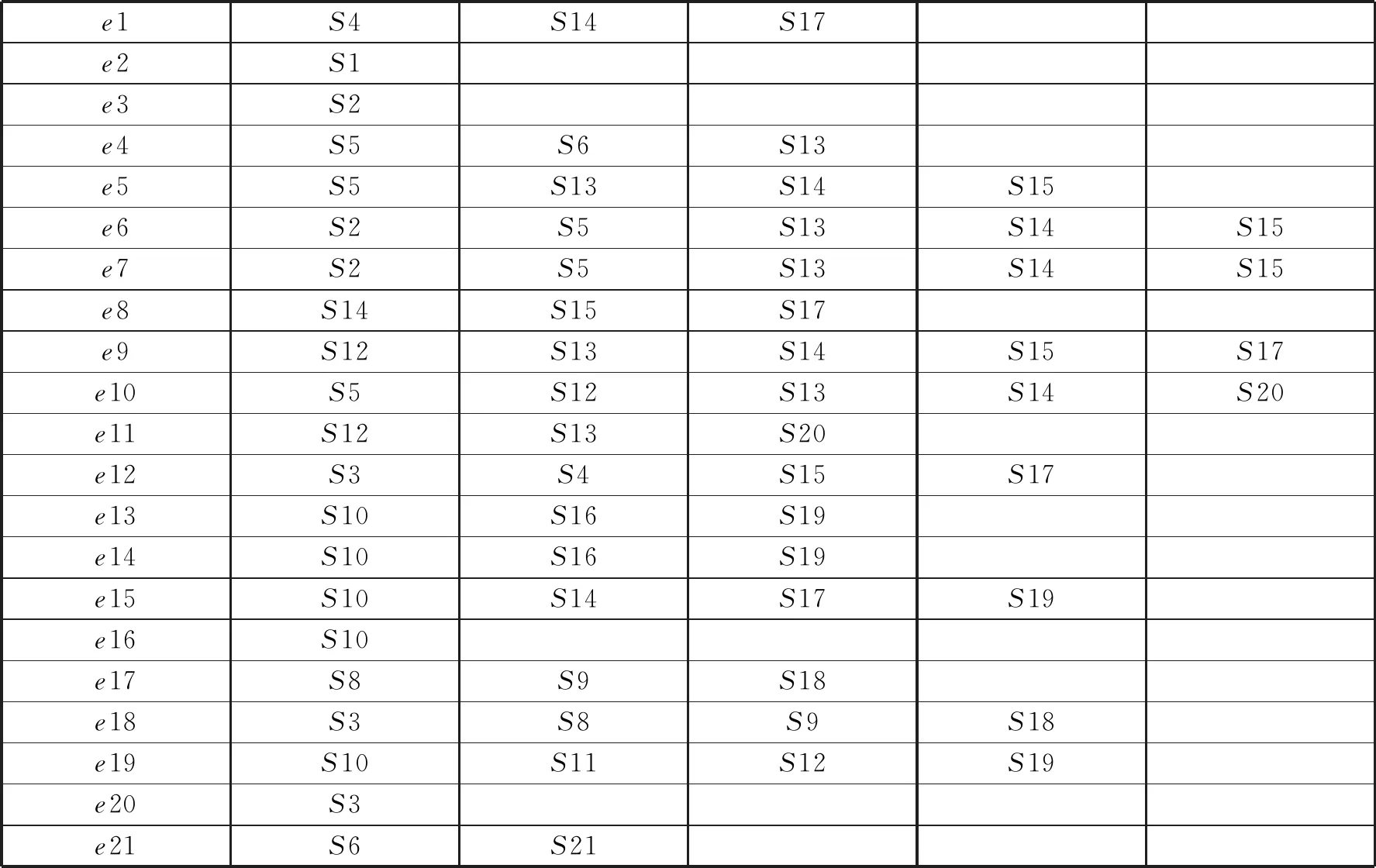
表4 货物供应点集合

表5 Lingo运行结果

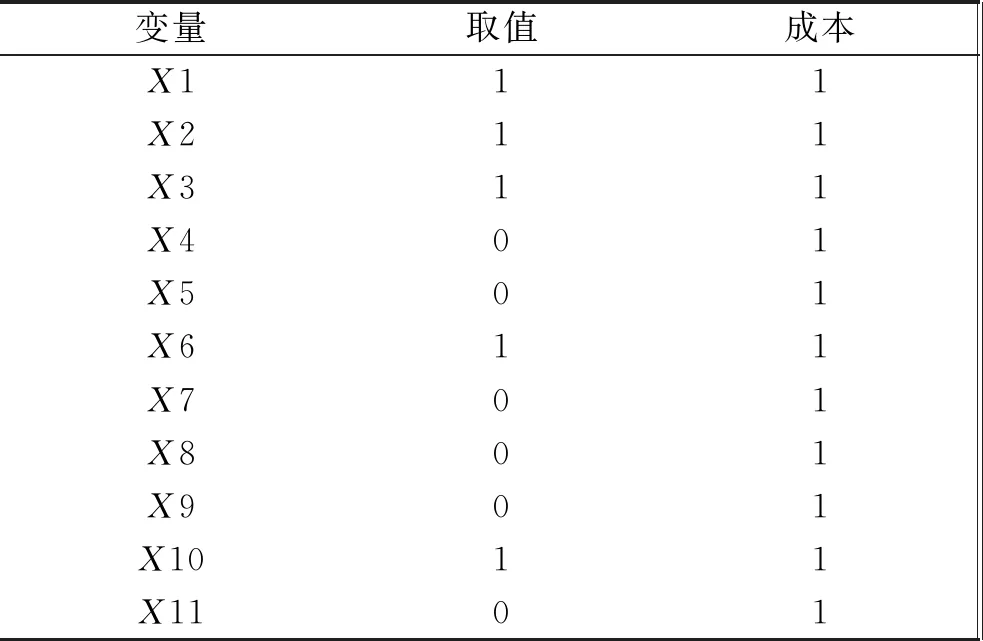
变量取值成本X111X211X311X401X501X611X701X801X901X1011X1101

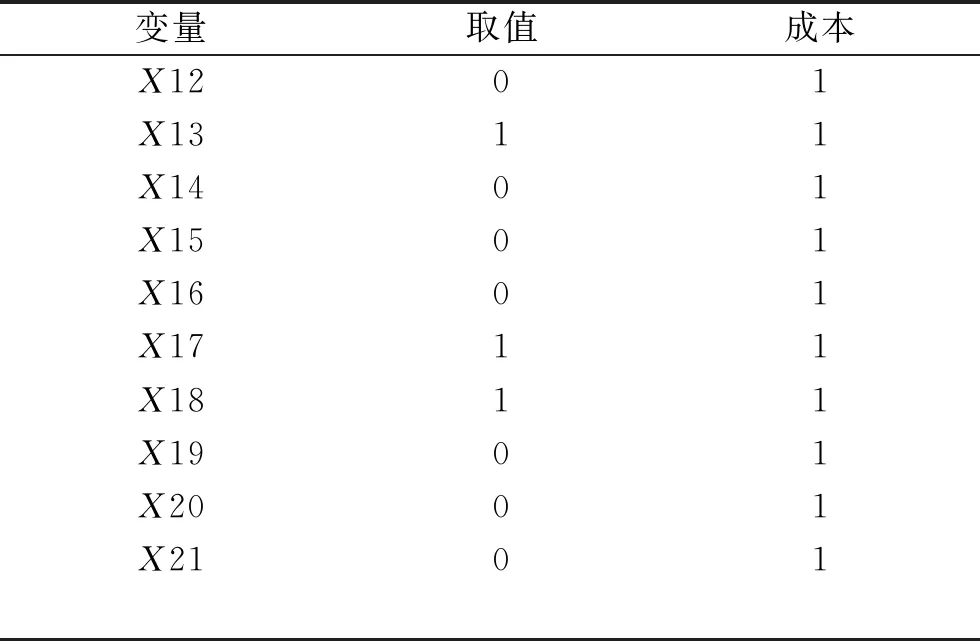
变量取值成本X1201X1311X1401X1501X1601X1711X1811X1901X2001X2101

由上面0-1整数规划算法的求解结果可以看出，最少需要S1、S2、S3、S6、S10、S13、S17、S18这8个物流供应点才能全覆盖所有货物需求点。最终选中的网络节点分布情况如图2所示。

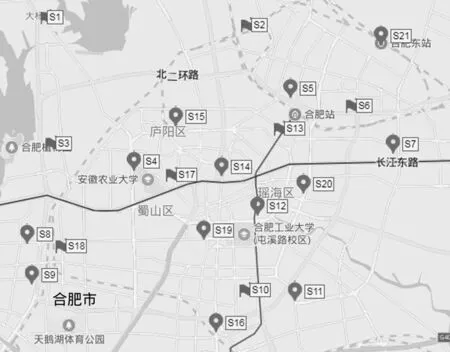
图2 最终网络节点分布图

6 结论

通过分析以往文献了解到选址问题所用的模型及相关算法，在对比分析各种算法优缺点的基础上，采用0-1整数规划算法对模型进行求解。以合肥市二环及周边区域的数据为例进行了实证分析，最终得到了地下物流系统网络节点分布图。城市地下物流系统网络节点的选址涉及到多方面的因素，包括当地物流业的分布、商品流向、政府政策、科技水平等。研究考虑的范围有限，在现实的网络节点选址中应该集多人的力量从更多的角度剖析问题，这样才能做出更加科学、全面的考虑。