穿刺力检测传感器解耦方法研究

许 曙，许德章，梁 艺

(1.安徽工程大学 机械与汽车工程学院，安徽 芜湖 241000;2.芜湖安普机器人产业技术研究院有限公司，安徽 芜湖 241000;3.先进数控和伺服驱动技术安徽省重点实验室，安徽 芜湖 241000)

在微创外科手术中，主治医生进针操作完全凭借个人经验，难以通过语言和示范等形式传授给见习医生。通过技术方法实时检测进针过程的操作力，完整地记录和直观地显示进针操作力，辅助医生完成穿刺手术，对于微创外科临床实践具有重要应用价值和学术意义。辅助针穿刺系统有利于提高医生进针过程的稳定性，减轻医生劳动强度，减小创伤截面，加快患者手术恢复[1]。不同肌肉和组织层阶的力学性质不同，表现出不同进针阻力特性。另外，为了达到更好的手术效果，不同肌肉和组织层阶应采用不同的进针力。因此，实时识别进针阻力是满足不同层阶穿刺要求，及时调整进针策略的首要条件。

穿刺力检测选用电阻应变片式六维力传感器，传感器弹性体形变转换为应变片电阻值的变化，利用惠斯通电桥转换输出电信号，再经过放大电路和滤波电路，得到电压输出信号[2]。弹性体的结构、机械加工精度、应变片规格、贴片工艺等因素将导致维间信号存在耦合，影响传感器测量精确度。标定和数字处理是实现六维力传感器解耦，提高测量精度的关键环节。六维力传感器标定需要借助标定实验台，完成标定数据采集。在六维力传感器标定实验台研究方面，国内外研究单位取得了积极进展，中国科学院合肥智能机械研究所[3]在国内率先研制出静态砝码标定实验台，东南大学宋爱国[4,12]研制出砝码重锤式标定实验台，合肥工业大学[5]也研制出类似标定试验台；北京强度研究所刘砚涛[6]采用液压加载方式，研制出液压标定实验台；郭凯[7]等采用虚拟仪器技术，在标定实验台基础上添加了数据处理功能，推出了六维力传感器静态校准实验系统。针对多维力传感器解耦的问题，国内外学者做了大量探索性研究，C.Oddo[8]等基于小二乘法降低传感器耦合噪声，合肥智能机械研究所[9-10]采用神经网络线性模型，通过样本数据训练学习方式获得耦合权重矩阵；Osama Al-Mai[11]等采用最小二乘法(LSM)，建立了耦合模型，获得解耦矩阵。

在穿刺手术实施过程中，进针力非常小。为了提高传感器的灵敏度和测量精度，要求传感器弹性体的尺寸设计得比较小；另外，为了便于医生操作和使用，要求传感器机械结构尽可能紧凑。因弹性体尺寸小，各电阻应变片粘贴的间距也很小，导致维间耦合迅速增强；多维力传感器量程较小，耦合误差容易淹没微小的测量信号，对解耦精度提出了更高要求[13-14]；因此，用于穿刺力检测的多维力传感器，在标定和解耦环节，需要采取相应的技术措施才能满足解耦精度的要求。

研究所用穿刺力检测传感器线性力量程30 N，转矩30 N·cm量程。在传感器标定过程中，选用了6位半精密电压表，直接读取各维放大电路输出的电压信号，采用人工判读和后续数据处理，没有采用计算机A/D转换的数字值，避免A/D转换过程噪声信号混入。针对穿刺力传感器量程小、耦合程度高的不利因素，设计了一款专用标定实验台。在传感器标定过程中，逐一施加单方向载荷，测出各路输出的电压信号，绘制载荷和信号关系图，人工判读维间耦合关系，优化加载点，筛选标定数据，选择耦合程度低的测量数据，再解算矩阵。

1 解耦原理

假设输入和输出呈线性关系，即传感器受力与其输出的电压信号呈线性关系。在上述假设的基础上，即传感器承受的力与其输出信号的电压值呈比例，满足以下数学模型

F6×6=C6×6×Si×j,

(1)

式中，F代表传感器承受的力;S代表传感器输出信号的电压值;C代表转换矩阵，即解耦矩阵。解耦是测量的逆过程，即已知F和S，求解矩阵C。

C6×6=F6×6×(Si×j)-1,

(2)

为了便于求出C矩阵36个元素，采取单一方向逐次加载，测量6个通道(六维)输出电压信号的方式，确定C中某一行6个元素的值。因Fx、Fy和Fz标定过程相同，现以Fx方向为例，阐明标定原理。

(3)

仅在Fx方向施加力时，测出(s11s21s31s41s51s61)T，得到式(4)：

c11s11+c12s21+c13s31+c14s41+c15s51+c16s61=Fx,

(4)

显然，一次加载和标定，无法确定式(4)中6个未知数c11、c12、…、c16。因此，需要在传感器量程范围内，取6个标定点，逐个加载标定，获得6个方程组成方程组，才能确定式(4)中6个未知数。

因在加载Mx和My力矩过程中，Y和X方向分别伴随一个线性力，以Mx力矩加载为例，存在式(5)关系：

(5)

其中，(m41m42m43m44m45m46)T为Fy+Mx，

(6)

式(5)中的m14、m24、…、m64分量分别减s14、s24、…、s64，得到仅包含Mx力矩的关系式(6)，可实现Mx方向单一加载的目的。

为了方便数据处理，对输出电压矩阵[S]做归一化处理，得到式(7)：

(7)

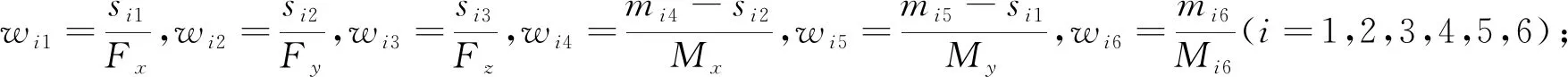
(8)

由式(8)可知，W6×6为耦合矩阵，W6×6逆矩阵为解耦矩阵C6×6。

2 标定实例

2.1 实验标定系统

借助回转刀架的回转和分度功能，组建的实验标定系统如图1所示。选用DMM-M3065型6位半精密电压表，直接测量传感器六路放大电路输出信号的电压值。选用普源M300系列数据采集/开关，实现测量通道切换，轮流测量传感器六路放大电路输出信号的电压值。

2.2 预标定

为了验证假算的合理性，以Fx方向为例，开展预标定实验。在已知载荷Fx大小和输出电压值(s11s12s13s14s15s16)条件下，解算(c11c12c13c14c15c16)6个未知数。穿刺力检测传感器尺寸为Ø80 cm×50 cm，结构如图2所示。Fx和Fy最大量程为16 N，Fz最大量程为30 N，Mx和My最大力矩为15 N·cm，Mz最大力矩为30 N·cm。

图1 传感器标定系统图2 穿刺力检测传感器结构图

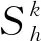
2.3 标定过程

依据前文标定原理，Fx、Fy、Fz和Mz可以施加单一载荷，Mx和My在加载过程中伴随附加线性力，Fx、Fy、Fz、Mz及Mx、My按两类性质载荷逐一加载，标定传感器，求解解耦矩阵。将6个测量通道调零。

(1)调整三爪卡盘，使Fx垂直于地面，加挂砝码，在Fx正方向施加载荷。

(2)Fx正方向依次悬挂4.9 N、9.8 N、14.7 N、9.8 N、4.9 N、9.8 N、14.7 N砝码，依次读取6个通道输出信号的电压值，完成Fx正方向标定。标定点与6个通道输出信号电压值对应关系如表2所示。

(3)调整三爪卡盘位置，依次悬挂4.9 N、9.8 N、14.7 N、9.8 N、4.9 N、9.8 N、14.7 N砝码，依次读取6个通道输出信号的电压值，完成Fx负方向加载。

(4)调整三爪卡盘，标定Fy分方向，正负加载点选择与Fx方向标定点一致。

(5)Fz只标定正方向，标定点依次选择9.8 N、19.6 N、29.4 N、19.6 N、9.8 N、19.6 N和29.4 N。

(6)在Fx方向施加正负相等的偏心力，Fx方向正负线性力相互抵消，只产生Mz等效力矩，偏心距离L选择30 mm。Fx方向加载点选择4.9 N、6.86 N、8.82 N、6.86 N、4.9 N、6.86 N、8.82 N，对应Mz的等效力矩分别为14.7 N·cm、20.58 N·cm、26.46 N·cm、20.58 N·cm、14.7 N·cm、20.58 N·cm、26.46 N·cm。为了消除Fx单一方向加载形成的不对称误差，在Fy方向选择与Fx相同的标定点，再做一次标定。Fx和Fy方向同一加载点的测量结果求平均。

(7)在Fy分方向施加偏心力，偏心距离L选择50 mm，产生Mx力矩。Fy偏心力选择0.98 N、1.96 N、2.96 N、1.96 N、0.98 N、1.96 N、2.96 N标定点，在Mx+方向产生4.9 N·cm、9.8 N·cm、14.7 N·cm、9.8 N·cm、4.9 N·cm、9.8 N·cm、14.7 N·cm等效力矩。

(8)My加载方式和标定点选择与Mx一致。

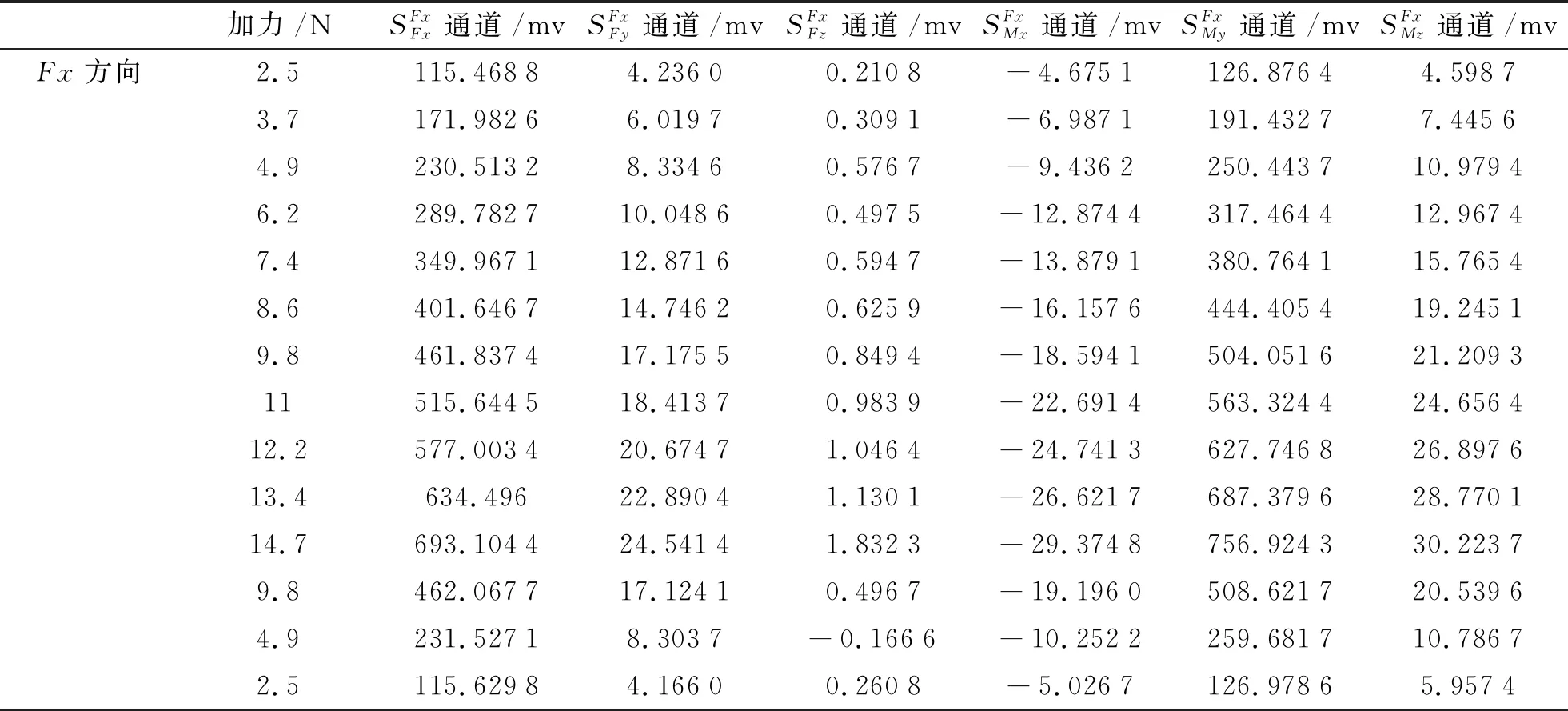
表1 Fx方向载荷电压表

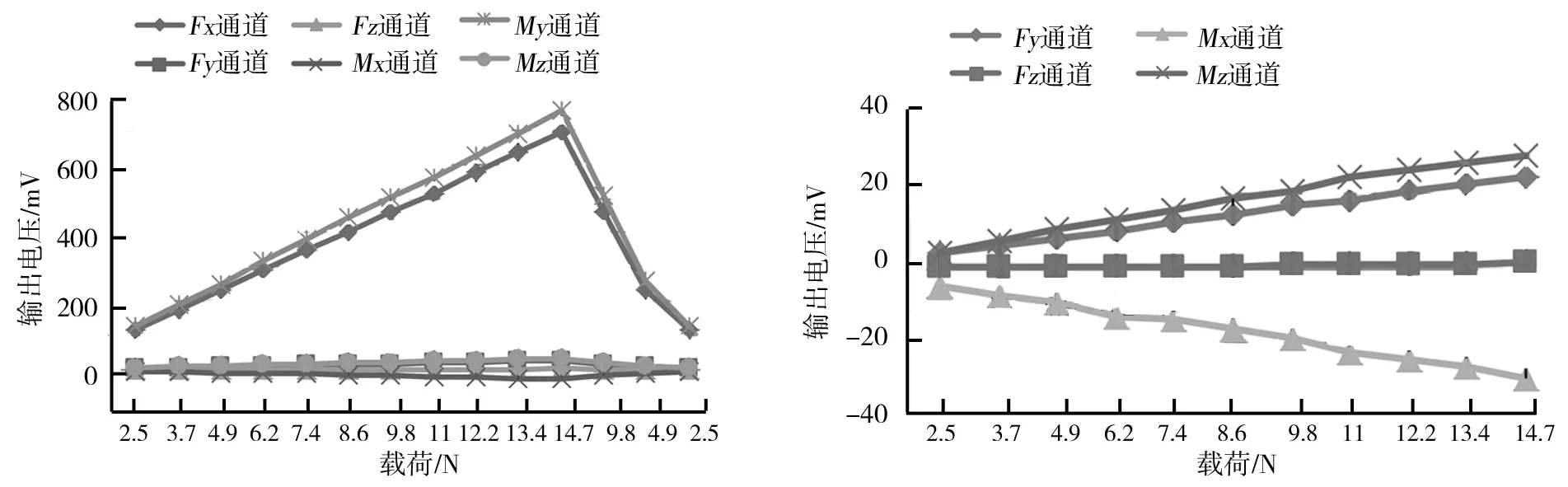
图3 Fx载荷图 图4 Fy、Fz、Mx和Mz方向输出放大图

2.4 数据处理

在一个单一方向施加载荷，6个方向都有电压输出信号，在Fx+方向依次施加4.9 N、9.8 N、14.7 N、9.8 N、4.9 N、9.8 N、14.7 N载荷，各通道输出电压如表2所示。

选择适当标定点，完成Fy、Fz、Mx、My和Mz方向加载，得到与表2类似的输出关系。依据前文所述的传感器标定原理，对输出电压矩阵做归一化处理，得到表3。

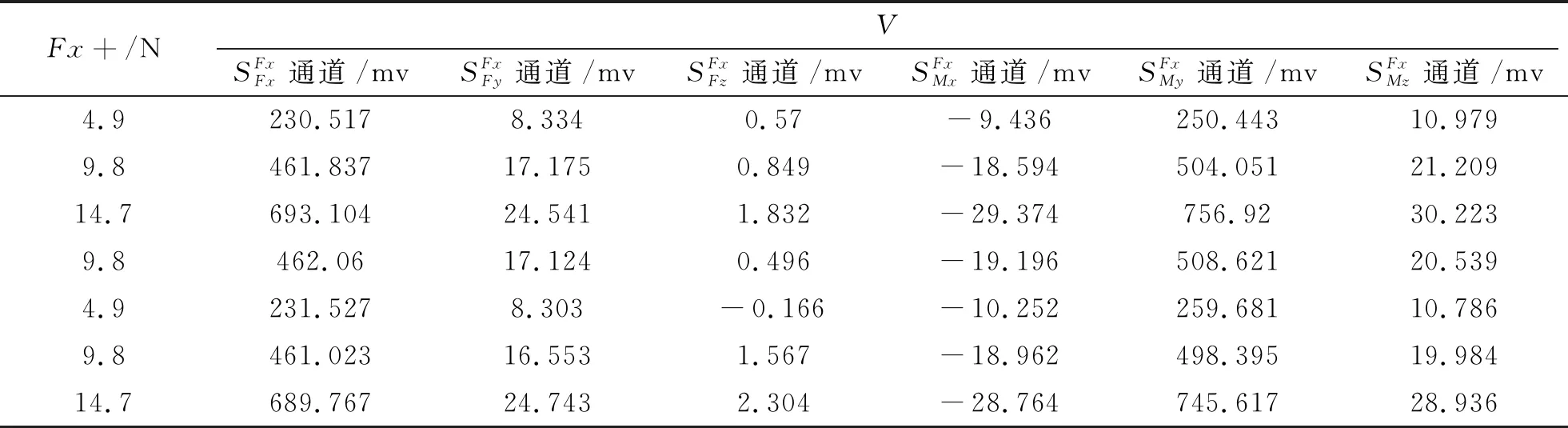
表2 Fx+方向载荷与输出电压的对应关系

Mx和My在标定过程伴随偏载力矩，依据关系式(6)消除偏载力矩后，表3的数据转换成表4。此时，各通道施加的力或力矩等效为单一载荷。

表4 等效单一载荷归一化结果

结合表3和表4，针对6个加载方向的正、负标定点做平均化处理，获得的结果如表5所示。表5的数据与关系式(7)中的W6×6矩阵内各元素对应。求W6×6的逆矩阵，得到标定矩阵[C]。标定矩阵[C]各元素具体如表6所示。

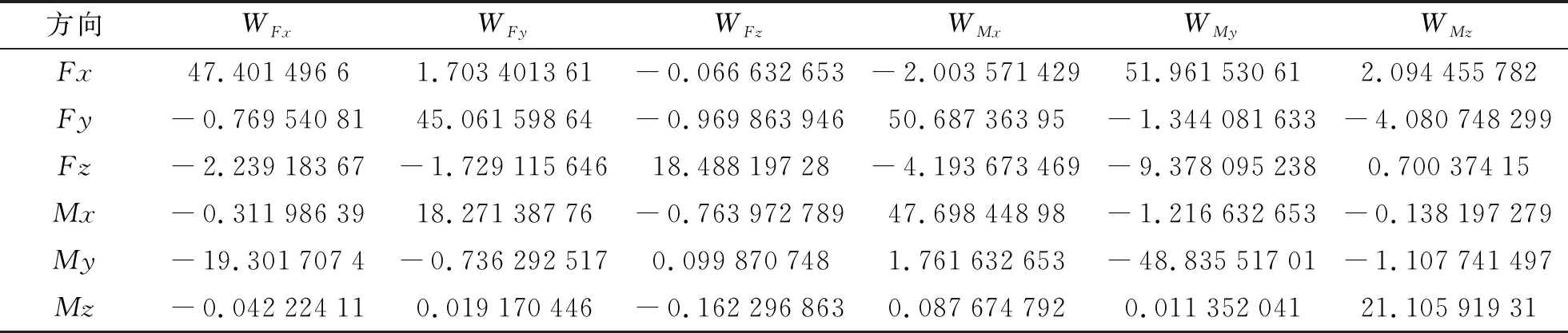
表5 平均化结果

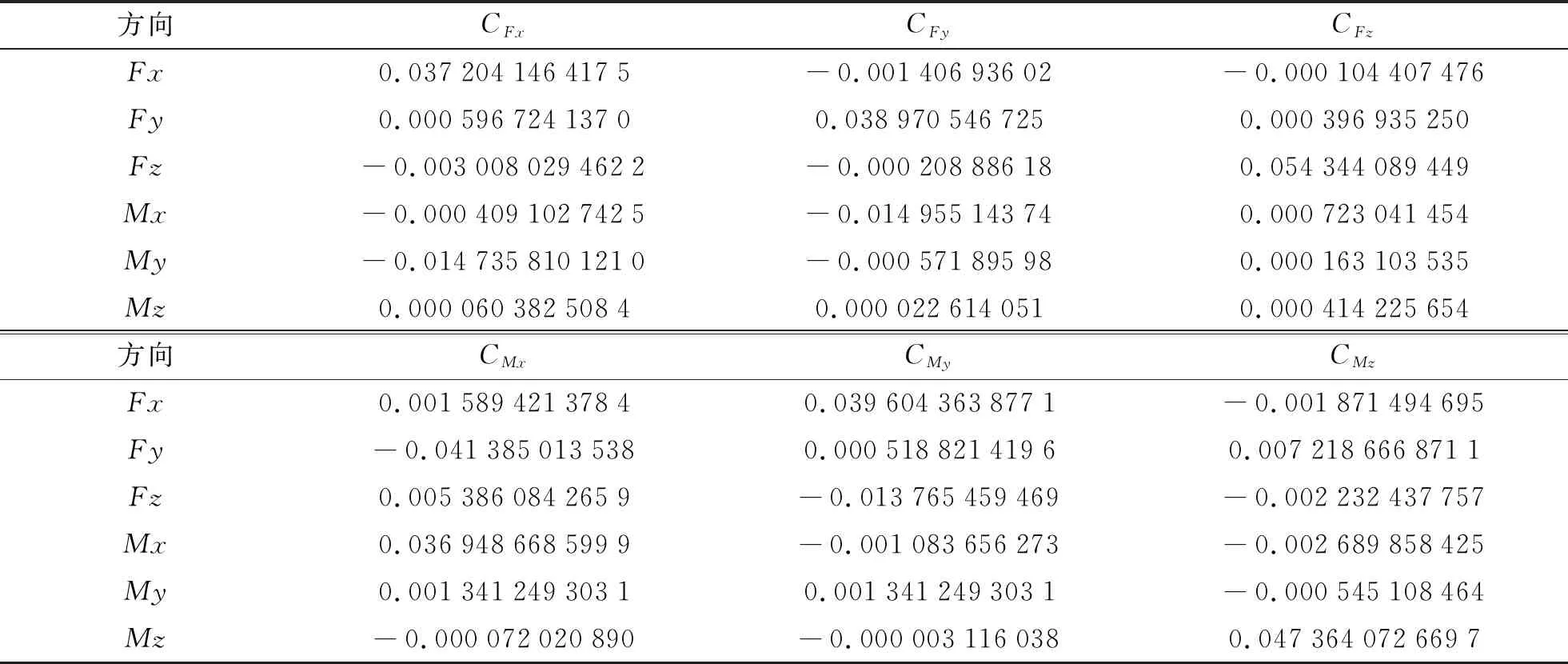
表6 逆矩证

3 结论

研究以穿刺力检测传感器为对象，采取单方向逐次加载的方法，针对力矩加载过程中的附加线性力，采取了附加线性力消除措施，推导出六维传感器的解耦矩阵。选用精密分度刀架，构建了可单方向逐次加载的标定装置。针对小量程多维力传感器标定过程中存在耦合性强、线性度差等困难，采取优化标定点，选用六位半精密电压表，直接测量传感器放大电路输出信号的电压值等措施，有效地提高了传感器的标定精度。预标定曲线表明，传感器的输入和输出呈现良好的线性关系，求解的耦合矩阵有效地消除了各维间的耦合关系。