压电微动平台的极点配置PID控制

2019-12-17周鹏飞崔玉国惠相君汪家乐孙靖康

压电与声光 2019年6期

周鹏飞，崔玉国，惠相君，汪家乐，孙靖康

(宁波大学机械工程与力学学院，浙江宁波 315211)

0 引言

微动平台是一种能够实现亚毫米级运动行程、纳米级分辨率的微位移机构。在精密与超精密测量中，它可用于对传感器进行精密位置调节[1-2]；在微机电系统(MEMS)装配中，它可实现微零件的装配[3-4]。压电微动平台通过压电执行器驱动其弹性机构来产生微位移及传递力，其具有体积小，输出力大和定位精度高等优点，比采用其他驱动形式的微动平台更具优势。

由于压电微动平台系统具有迟滞非线性，需要对其进行控制以提高位移输出精度，目前常用的控制方法有前馈控制，比例、积分、微分(PID)控制，鲁棒控制，自适应控制及复合控制等。Ming等[5]采用基于改进Bouc-Wen模型的前馈控制，对压电微动平台进行正弦波轨迹跟踪，跟踪误差达到0.68%。Lee等[6]采用PID对压电微动平台进行控制，在跟踪幅值为10 μm的正弦轨迹时，跟踪误差为50 nm。Edardar[7]采用模型参考自适应控制对压电微动平台进行轨迹跟踪，使平台在跟踪幅值为25 μm的三角波时，最大跟踪误差为0.55 μm。张栋等[8]采用基于自适应神经网络的PID控制，使平台在跟踪幅值为25 μm的正弦波时，平均误差为0.80 μm。周淼磊等[9]采用神经网络控制与专家模糊控制的复合控制方法，在对平台进行任意输入跟踪时，最大跟踪误差达到0.26%。于志亮等[10]采用PI模型与增量式PID控制算法结合的复合控制，使压电微动平台跟踪在 100 Hz正弦曲线时，跟踪误差≤0.59%。

在上述控制方法中，作为开环控制的前馈控制算法简单，成本低，但其控制效果过于依赖模型精度；作为闭环控制的PID控制、最优控制、鲁棒控制、自适应控制可使压电微动平台的迟滞误差接近于0，但需要精密的传感器。复合控制是结合前馈控制和闭环控制的控制方法，可进一步提高平台的定位控制精度，但比单一的控制算法复杂。其中，PID控制在工程实际中工作可靠，便于调整，且不依赖被控对象精确的数学模型，但现有的PID参数整定方法都是基于经验或试凑设计，这些设计方法参数选择耗时且较粗略。

基于极点配置的PID控制器参数整定方法，可使PID参数与系统性能指标相联系，具有快捷、准确的优点。本文采用该方法设计压电微动平台的PID控制器，对平台进行控制，以提高其定位精度。

1 平台系统动力学建模

平台系统包括压电执行器和微动平台。首先通过对压电执行器建立并辨识其数学模型，进而在对平台进行受力分析、运动分析的基础上，建立并辨识平台系统的动力学模型。

1.1 压电执行器建模

压电执行器主要在静态或低频情况下工作，在电学上可以等效为电容和绝缘电阻的并联。图1为压电执行器的等效电路。在考虑驱动电源内阻Ro远小于压电执行器内阻Rp的情况下，可得

(1)

式中：τ=RoCp为时间常数；U(s)、Uo(s)分别为电源控制电压u(t)、驱动电压uo(t)的拉式变换；a为驱动电源放大倍数。

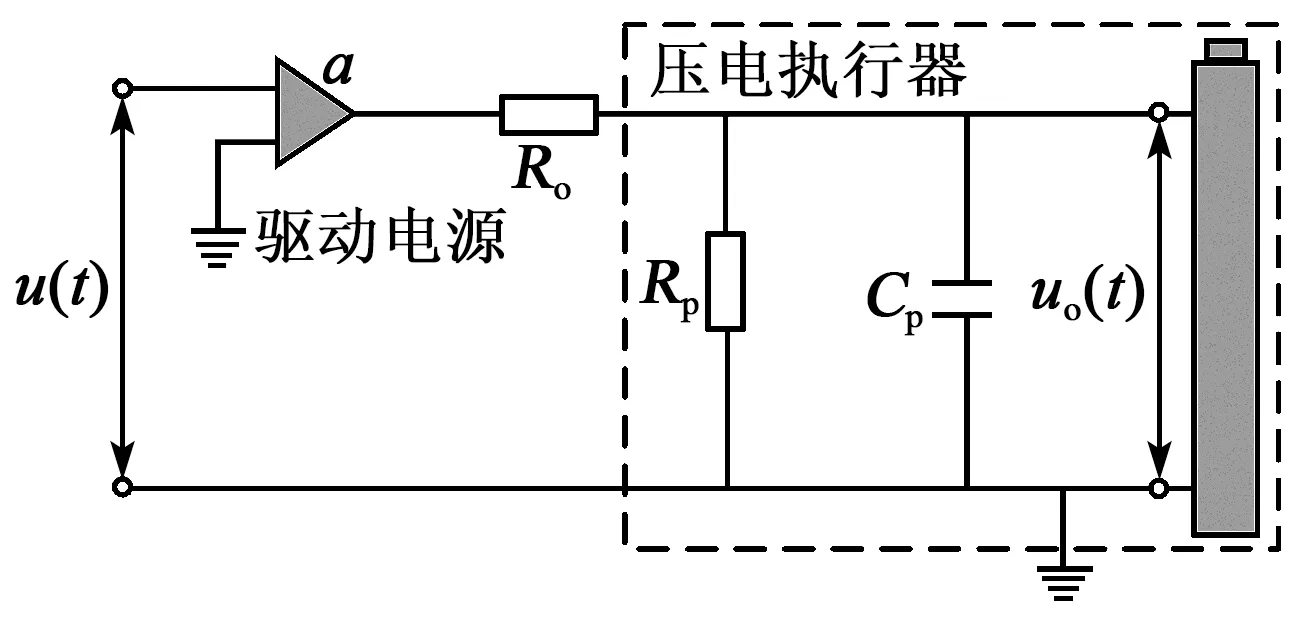
图1 压电执行器的等效电路

在uo(t)作用下，当压电执行器两端被完全固定时，其输出位移将全部转化为压电执行器输出力fp(t)，故可得

(2)

式中：n为压电执行器层数；d33为压电应变常数；kp为压电执行器的刚度；Fp(s)为fp(t)的拉式变换。

由式(1)、(2)可得压电执行器的传递函数为

(3)

给空载压电执行器施加阶跃电压，便可辨识出nd33a及τ。已知式(3)中kp=60 N/μm，故u(t)到fp(t)的传递函数为

(4)

1.2 平台建模

压电执行器对平台的作用力f(t)与压电执行器的空载位移δ0(t)、压电执行器驱动平台时的输出位移δ(t)之间的关系为

f(t)=kp[δ0(t)-δ(t)]=fp(t)-kpδ(t)

(5)

根据式(5)，同时考虑压电执行器的阻尼，可得平台沿x(或y)方向的质量-弹簧-阻尼模型(见图2)。

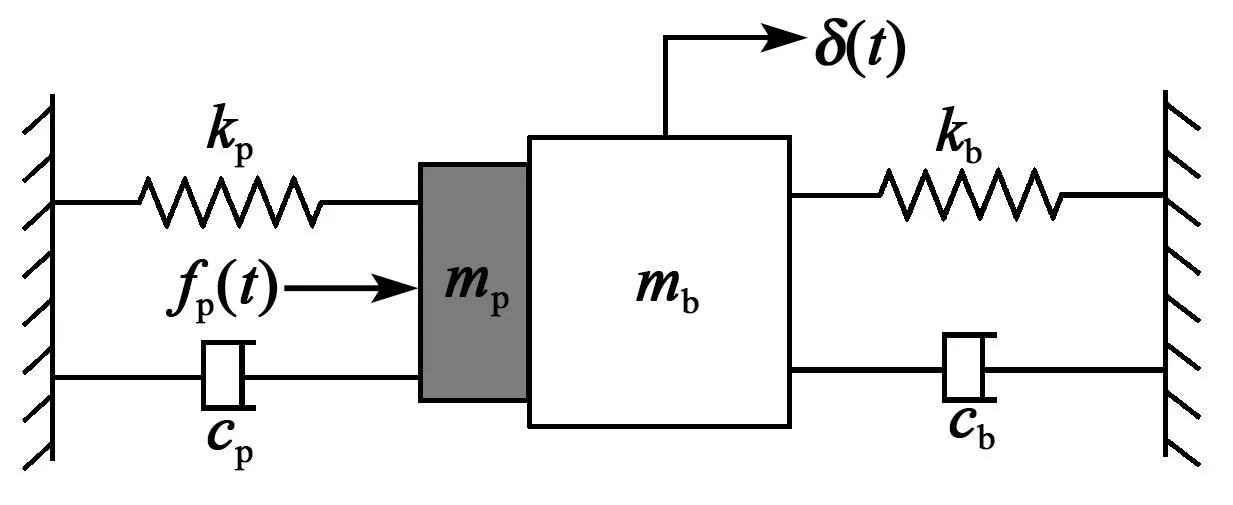
图2 平台的等效模型

根据图2可得δ(t)与fp(t)之间的传递函数为

(6)

其中

(7)

(8)

式中：Δ(s)为δ(t)的拉式变换；ωn,ξ分别为平台的固有频率、阻尼比;mb、cb、kb分别为平台的运动质量、阻尼、刚度;mp、cp、kp分别为压电执行器的质量、阻尼、刚度。

在通过给平台施加力测得其kb，通过脉冲响应法测得平台的ωn，通过半功率法测得ξ的情况下，可得微动平台的作用力与输出位移之间的传递函数为

(9)

1.3 平台系统动力学模型

由式(4)、(9)可得平台系统的传递函数为

(10)

2 平台PID反馈控制

2.1 PID控制原理

PID控制通过对偏差的PID的线性组合实现对被控对象的控制。离散PID控制律为

(11)

式中：KP为比例增益；TI为积分时间常数；TD为微分时间常数；k、k-1分别为采样时刻kT、(k-1)T的简写；T为采样周期；u(k)为k时刻PID控制器的输出；e(k)、e(k-1)分别为k、k-1时刻的偏差。

为使PID控制过程占用内存小，耗时短，将式(11)中的k换成k-1，然后再同式(11)相减，可得具有递推关系的PID表达式为

u(k)=u(k-1)+g0e(k)+g1e(k-1)+

g2e(k-2)

(12)

其中

g0=KP(1+T/TI+TD/T)

(13)

g1=-KP(1+2TD/T)

(14)

g2=KPTD/T

(15)

对式(12)进行z变换，得到有递推关系的PID控制器的z传递函数为

(16)

2.2 平台PID控制器设计

由式(10)可求得平台模型的3个开环极点，如图3所示。图中，P01为压电执行器模型的实数极点，P02、P03为平台模型的两个共轭极点。这3个极点都处于虚轴左侧，由此可知系统稳定。平台为二阶振荡环节，其模型的两个共轭极点离虚轴较近，使得系统的开环阻尼效应较弱，导致可动部分振动持续时间较长。由此可见，需对平台模型的两个共轭极点进行重新配置。

图3 平台模型的极点分布图

式(10)可进一步可表示为

A(z-1)δ(k)=z-2B(z-1)u(k)

(17)

其中

A(z-1)=1+a1z-1+a2z-2

(18)

B(z-1)=b0

(19)

a1=2ξωn-2

(20)

(21)

(22)

式(16)可进一步表示为

P(z-1)u(k)=G(z-1)δr(k)-G(z-1)δ(k)

(23)

其中

P(z-1)=1-z-1

(24)

G(z-1)=g0+g1z-1+g2z-2

(25)

式(23)是极点配置控制器方程，其结构框图如图4所示。

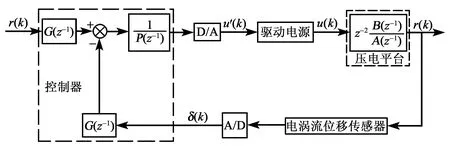
图4 平台控制系统的构成框图

将式(23)代入式(17)，可得：

[A(z-1)P(z-1)+z-2B(z-1)G(z-1)]δ(k)=

z-2B(z-1)G(z-1)δr(k)

(26)

设闭环特征多项式为Q(z-1)，Q(z-1)的零点就是理想的闭环极点，于是：

A(z-1)P(z-1)+z-2B(z-1)G(z-1)=Q(z-1)

(27)

根据极点的配置原理，式(27)中的P(z-1)必须满足P(1)=0，G(z-1)必须是z-1的二次多项式。因此，G(z-1)可由式(25)确定，而P(z-1)为

P(z-1)=(1-z-1)(1+p1z-1)

(28)

式中：(1+p1z-1)可看作是滤波器；p1为待定滤波器系数。

将式(18)、(19)、(25)、(28)代入式(27)，可得：

(1+a1z-1+a2z-2)(1-z-1)(1+p1z-1)+

z-2b0(g0+g1z-1+g2z-2)=

q0+q1z-1+…+qnz-n

(29)

因为平台为二阶振荡环节，故本文选择n=2。式(29)中，q0=1，通过极点配置可确定q1、q2。如图5所示，如果保持平台极点的虚部不变，将其实部沿着实轴方向平移，就能将所期望的闭环系统极点以最短的距离最大程度地远离虚轴。本文将系统闭环阻尼比取为1，根据图5所示的极点配置法，平台的闭环极点如表1所示。