复合材料结构与表面压电材料动态布局优化
2019-12-17单尧,余兵,牛斌
单 尧,余 兵,牛 斌
(1.大连理工大学 机械工程学院,辽宁 大连 116024;2.上海宇航系统工程研究所,上海 201109)
0 引言
工程结构大多处在动态载荷环境中,结构受动态载荷产生的振动会影响结构的性能与使用寿命,所以抑制结构的振动具有重要意义。压电材料是一种可实现机械能与电能相互转化的智能材料。压电材料的逆压电效应可以将电能转换为机械能,利用该特性,压电材料被广泛用于主动或被动控制结构振动[1]。通过优化结构本身材料的分布实现最小化结构振动响应的研究已得到广泛研究[2]。近年来,学者们通过引入压电材料来改善结构的动态性能,如Kang和Zhang通过优化结构表面压电材料的分布研究了结构振动的主动控制[3]。由于脆性压电陶瓷材料的可加工性差,所以难以实现加工任意拓扑的压电片,因此,一些学者提出了通过优化指定规格压电片的布局代替寻找最优的压电材料拓扑,如Quek等[4]利用直接搜索法得到了抑制结构指定模态自由振动的压电片的最优分布;Gao等[5]利用遗传算法研究了抑制振动板噪声传递的压电传感器与致动器的位置优化问题。文献[2-5]的研究工作主要通过单独优化支撑结构的拓扑或结构表面的压电材料分布实现结构的振动抑制。本文将优化复合材料支撑结构的铺层与材料选择,同时优化结构表面给定尺寸的矩形压电片布局,实现最小化结构振动响应。数值算例表明,使用该优化方法可提高结构振动抑制的效果及优化设计的制造性。
1 压电结构振动分析
压电材料的压电效应可分为正压电效应(机械能转化成电能)与逆压电效应(电能转化成机械能)[6],分别表示为
D=eε+κE
(1)
σ=Cε-eE
(2)
式中:ε,σ分别为应变向量与应力向量;C为弹性矩阵;e,κ分别为压电应力常数矩阵和介电常数矩阵;E,D分别为电场强度向量与电位移向量。

图1 复合材料层合板示意图与横截面图
本文采用压电材料作为致动器,与外加电压相比,由压电材料正压电效应产生的电荷量非常小,对压电材料的作用可忽略不计。因此,我们只考虑压电材料的逆压电效应。针对图1所示复合材料层合结构,只考虑压电材料的逆压电效应[7],利用有限元法得到的压电感应力向量fin为
fin=-Kuφφ
(3)
式中Kuφ,φ分别为压电矩阵和电势。
不考虑阻尼,引入压电材料后振动结构的控制方程为
(4)

2 振动作用下压电结构优化列式
2.1 离散材料优化(DMO)法材料模型
与各向同性材料不同,复合材料具有方向性。所以,复合材料结构的性能与每一层的纤维分布与铺设角度有关。在这里对于复合材料结构的建模我们参考DMO法[8],这种方法通过选择预先设定的备选材料来实现复合材料结构的铺层材料、铺设角度及铺层顺序的优化;其中备选材料可以是不同种类的材料,也可以是铺设角度不同的同一种纤维增强复合材料。本文通过将备选材料设置为泡沫材料和不同铺设角度的纤维复合材料,实现各层不同纤维角度的分析与优化,以及纤维材料和泡沫材料的拓扑设计。应用DMO法后每层的本构关系矩阵Ql与质量密度ml分别为

(5)
(6)
式中:ξi,Qi和mi分别为第i种备选材料的权函数,本构关系矩阵和质量密度;nl为第l层备选材料总数。
本文中使用的压电材料为各向同性材料,基于DMO法我们将压电层备选材料设置为压电材料与人为定义的孔隙材料,并引入区域(Patch)设计变量[8],从而得到给定尺寸的矩形压电片的分布。第l层的压电应力矩阵el为
el=ξ1e1+ξ2e2
(7)
式中:ξ1,ξ2分别为压电材料和人为定义孔隙材料的DMO权函数;e1,e2分别为压电材料和人为定义孔隙材料的压电应力矩阵。
2.2 目标函数与压电结构优化列式
衡量结构振动的优化指标很多[9],选取结构局部位移作为描述结构振动响应的指标为
g=UTLU
(8)
式中:U为结构位移幅值向量;L为索引矩阵,表示需要优化响应节点的位置;上标T为转置运算。
引入式(8)与式(4),可得优化列式如下:
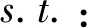
0 (9) 利用伴随法求得目标函数对设计变量的灵敏度为 (10) (11) 本节以图1所示结构作为算例来说明该方法的有效性。该结构(见图1)为左侧固定的层合悬臂板结构,共5层(每层厚为0.2 mm)。该悬臂板长为1 m,宽为0.5 m。将结构划分为40×20的有限元网格。第一层全为碳纤维复合材料,备选铺设角度为[0°,±45°,90°],第二层到第五层除了碳纤维材料,还有各向同性泡沫材料,第六层为各向同性的压电材料与人为定义的材料属性很小的孔隙材料。初始设计结构为各备选材料均匀分布。在悬臂板右端中心位置(A点)施加一个垂直板面的f=Feiωpt,F为外加机械载荷的幅值向量,其中幅值为10 N。根据初始结构的自由振动频率,选取激励频率为35 Hz(在第二、三阶的自由振动频率之间)。第六层的压电片厚为0.2 mm,长和宽均为50 mm。外加电压的频率和机械载荷的频率相同且幅值为1 V。选取全部节点的响应作为优化目标,即L为单位矩阵。压电材料的性能参数如表 1所示,η=40%。使用移动渐近线法(MMA)[10]求解式中的优化问题。压电材料、碳纤维复合材料和各向同性泡沫材料的弹性模量E、质量密度ρ、剪切模量G、泊松比υ及压电应力系数e分别如表1~3所示。 表1 压电材料性能参数表 表2 碳纤维复合材料性能参数表 表3 泡沫材料性能参数表 此模型在外激励频率35 Hz时得到的优化设计如图 2所示,其中第一层到第五层里的黑色短线代表碳纤维的铺设角度;第二层和第五层空白处为泡沫材料。第六层中黑色部分代表压电材料。灰色部分表示未粘附压电材料。 图2 35 Hz激励频率下优化设计结果 图3为优化前、后的结构在外激励频率35 Hz下的位移幅值分布对比图,为了使对比结果明显,图中显示的位移幅值为放大5倍后的结果。对比图3(a)、(b)可知,优化后的结构位移幅值明显小于初始结构。目标函数(g)由初始的20.84下降到0.046。对比图3(a)、(c)发现,压电材料的机械性能可以在一定程度上减小结构的振动响应。观察图2可看出,纤维材料和第六层压电材料片的分布具有较好的对称性;泡沫材料主要分布在中间层,即第二层到第四层;对比图3中的位移幅值分布图,图2中第五层的纤维材料与第六层压电层的材料主要分布在位移幅值较大的区域。该结果充分说明了该抑振方法的有效性。 图3 位移幅值分布图 在本文中,压电材料作为压电致动器使用,其正压电效应对结构振动产生的影响忽略不计。数值算例表明经过优化,结构的振动响应明显减小。同时优化压电材料的分布与结构本身可有效地实现结构振动最小化,其中压电材料的分布说明,由压电材料的逆压电效应产生的力不仅可以有效地抑制结构振动,且压电材料本身具有的刚度与质量也可以增强结构本身的机械性能。

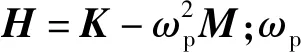

3 数值算例





4 结束语
