冻融循环条件下石灰改良土路基回弹模量研究

2019-12-17宋金华林园皓

重庆交通大学学报(自然科学版) 2019年12期

宋金华，林园皓

(河北工业大学土木与交通学院，天津 300401)

0 引言

石灰改良土在本质上属于重塑土，与施工期间相比，运营期间的路基路用性能会发生改变，同时其物理力学性质也不完全一样。季冻地区路基的力学性能受路基土体含水量、压实度、冻融循环次数和应力状况等的影响很大。作为表征路基刚度的重要指标，路基回弹模量可反映在重复的车辆荷载下路面结构的应力-应变关系，它也是国际上用来评估路面厚度设计的主要参数之一。有研究者提出：在修正路基回弹模量受干湿循环或冻融循环次数变化影响时可借用干湿循环或冻融循环强度折减系数[1-2]。受该观点启发，通过室内模拟试验，笔者参考折减强度的概念，对石灰改良土路基动回弹模量冻融循环折减系数进行了详细分析计算，深入研究了经历冻融循环后的石灰改良土路基回弹模量变化规律，对更深入地研究路基结构长期性能演变规律提供一定基础，同时对我国公路路基设计方法完善具有一定借鉴意义。

1 试验材料与方案

1.1 土样基本物理性质

试验土体取自于天津津北公路。津北公路修建在由吹填形成的海相沉积软土地基上，其主要由黏性土和淤泥质土组成，有机质含量丰富，含水量较高，多呈灰色，具有高压缩性和灵敏度、低渗透性、低强度等特点。为全面了解海相沉积软土的工程特性，笔者通过一系列常规试验得到了其基本物理指标，见表1。

表1 试验土体基本物理指标Table 1 Basic physical index of test soil

通过比重计法测定土样颗粒组成可知，粒径为0.05～2 mm砂粒占总质量的12%左右；粒径为0.002～0.05 mm粉粒占总质量的55%左右；粒径小于0.002 mm黏粒占总质量的33%左右。因此，土样呈现砂粒很少、黏粒较多、粉粒最多的规律，同时在砂粒组中基本上不存在大于0.2 mm的粗颗粒，故该土样属于不良级配土。这是其通透性差的重要原因之一。

1.2 土样准备

笔者按2%、4%、6%和8%这4种掺灰比将石灰(采用唐山新启建材有限公司的土壤改良CaO，其中CaO含量大于85%)与土进行初拌，再加适量蒸馏水，搅拌均匀并密封，浸润24 h。按照平衡含水率(equilibrium moisture content, EMC)、最佳含水率(optimal moisture content, OMC)与介于EMC及OMC之间的过渡含水率(transition moisture content, TMC)分别制作素土和石灰改良土试样，素土与改良土试样均按90%与96%的压实度压实。试样直径D=39.1 mm，高H=80 mm，采用三瓣饱和器分层击实后放在保湿缸中进行常温养护7 d[3]。

1.3 动回弹模量实验

根据沥青路面的应力状况与结构特点(表2)，制定路基土动回弹模量动态三轴试验加载顺序[4]。

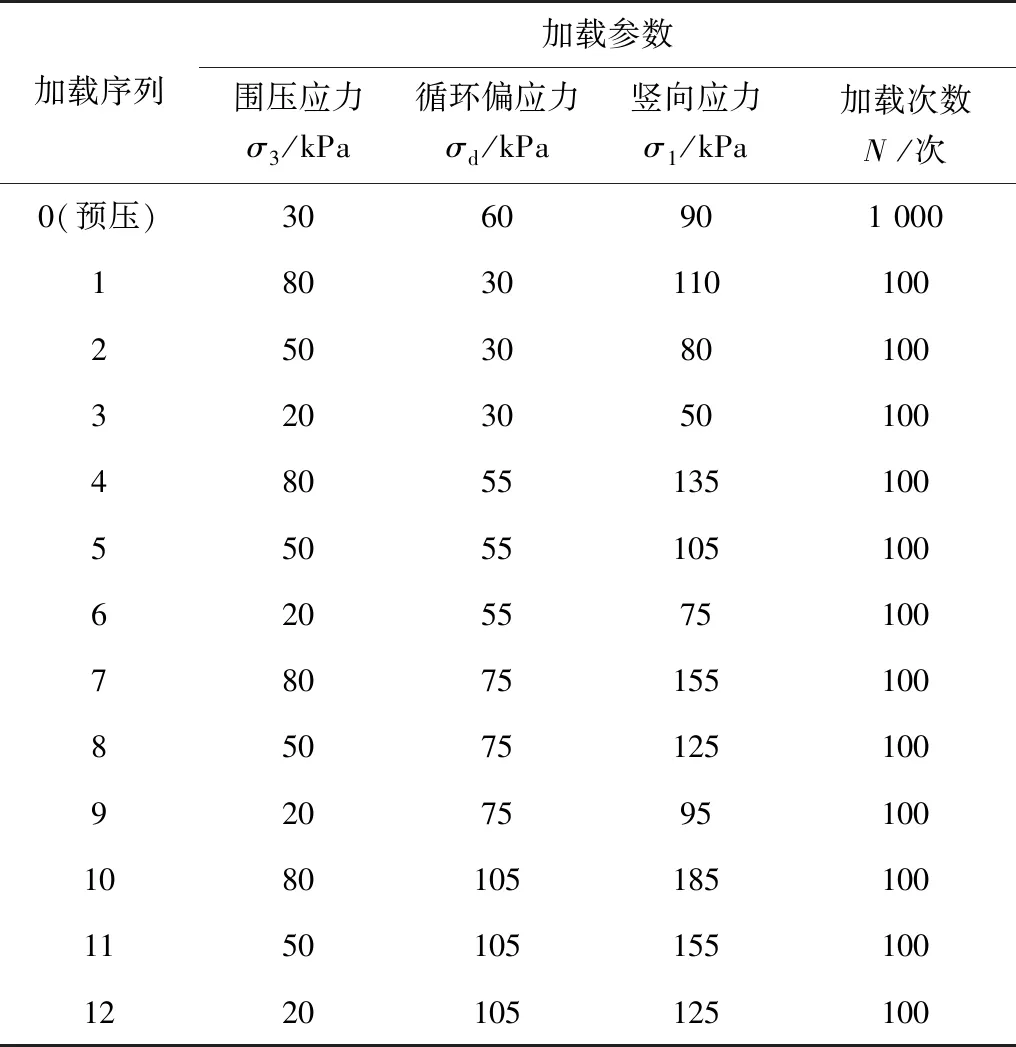
表2 加载序列Table 2 Loading sequence

为与季冻地区温度的变化状况接近，冻融温度设置为-15～5 ℃。冻融时，先将未冻融试样放入冻箱中，在-15 ℃下冻结12 h，再升温度至5 ℃，持续12 h，此过程为一次冻融循环。冻融次数设置为1、3、6、8、10，对冻融后的土体试样进行动三轴试验。此外，为深入了解冻融对路基土体回弹模量的影响，设置在相同条件下未冻融试样的动三轴对照试验。本试验输入振动频率为f=5 Hz的正弦波。

为便于分析临界动应力，并考虑到石灰改良土与素土的动力特性等因素，本试验设置动应力由30 kPa到50 kPa逐步提高，直至试样发生破坏。路基应力实际测量结果表明：基床表层的侧向压力较低，为20～60 kPa，因此施加的试验围压设置20、50、80 kPa这3级。剪切速率为0.5%/min，采用应变控制模式。按照SL237—1999《土工试验规程》[5]要求，将轴向累计应变达到5%时作为破坏标准。取100作为每级加载的循环次数，取应变水平稳定后的最后8次均值作为回弹变形。动回弹模量大小如式(1)：

(1)

式中：MR为动回弹模量；σd为轴向重复偏应力峰值，σd=σ1-σ3，σ1为最大主应力，σ3为最小主应力，分别对应着实验中的竖向应力和围压应力；εR为轴向回弹应变均值。

2 实验结果与分析

2.1 动回弹模量与应力状态关系

当黏质土试件在冻融循环次数N=1，掺灰比为4%(质量比，下同)，ωOMC=15%，ωTMC=17%，ωEMC=20%，压实度K=96%的条件下，回弹模量与应力状态的关系，如表3。

表3 4%石灰土动回弹模量与应力状态的关系Table 3 Relationship between dynamic resilience modulus and stress state of 4% lime soil kPa

在影响回弹模量的众多因素中，偏应力只是其中之一。通过分析可知：石灰改良土回弹模量受围压影响敏感程度要高于偏应力，随着围压应力增大、含水量减小而逐渐增大，随着重复荷载偏应力增加而有所降低。在OMC状态下，重复荷载偏应力对回弹模量影响并不显著；在TMC和EMC状态下，随重复荷载偏应力增加回弹模量出现降低趋势[5-6]。含水率从OMC状态转变为TMC状态时，回弹模量降低了35%～65%。从TMC状态转变为EMC状态时，回弹模量降低趋势并不明显。

2.2 随掺灰比、冻融次数和含水率变化规律

不同掺灰比的石灰土在围压σ=80 kPa，偏应力σd=30 kPa，压实度K=96%，OMC下，回弹模量随冻融循环次数与掺灰比变化关系如表4。

表4 不同掺灰比的路基土经过冻融后的动回弹模量Table 4 Dynamic resilience modulus of subgrade soil with different ash ratio after freezing and thawing

由表4可知：当试件掺灰比从0%增加到8%时，MR提高显著，掺灰比每增加1%，MR增加35%，当掺灰比达到6%时，回弹模量对掺灰比增加量的敏感程度降低。随着冻融次数增加，不同掺灰比下的动回弹模量均呈现下降趋势，经过6次冻融循环后，逐渐趋于稳定。掺入石灰对回弹模量的增大效果非常明显。在其他应力状态下的变化规律与此类似[7]。

当冻融次数不大于6时，试件每经历一次冻融循环，MR就会有一定程度降低。故定义石灰土路基经历冻融循环后的MR上、下限冻融次数分别为N=1、6时的MR值，即试件MR分别经历1～6次冻融循环后都还在该范围之内。

当N=1、6，掺灰比为6%时，试件在不同平衡含水率下MR分布如图1。由实验结果可知：当ωEMC=20%，ωTMC=±3%时，试件的MR在经历6次冻融循环之后有所降低，但大于20 MPa，其集中分布于20～40 MPa；当ωEMC=25%，ωTMC=±3%时，试件经历6次冻融循环后，MR降低幅度大，而且分布范围较广，其分布区域主要集中在0～30 MPa，试件在循环偏应力达到105 MPa时被破坏，认为此时MR=0[8]，因为不能得到合理有效的动回弹模量值。随着平衡含水率值增大，石灰路基土回弹模量受冻融循环影响程度不断增加。当平衡含水率值较小时，回弹模量受影响程度较小；当平衡含水率较大时，动回弹模量变化较为明显，而且趋于不稳定状态。

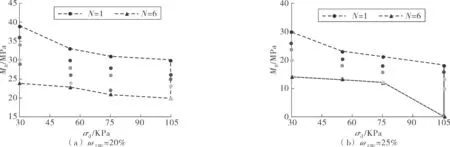
图1 不同平衡含水率下MR的分布区域Fig. 1 Distribution area of MR under different equilibrium moisture contents

2.3 石灰改良路基土冻融循环折减系数

鉴于季冻地区路基力学性能受冻融循环影响，随季节变化波动较大，目前研究动回弹模量湿度循环调整系数文献较多，而研究冻融循环变化对动回弹模量影响文献非常少，因此笔者在此基础上并结合强度折减系数概念提出了路基动回弹模量冻融循环折减系数。

笔者定义路基土冻融循环折减系数η为：在EMC状态下，经历冻融循环次数N后的路基回弹模量MR与初次达到EMC时的路基回弹模量MR1之比，如式(2)：

(2)

此处η仅反映路基动回弹模量取值受冻融循环次数影响。冻融循环对路基回弹模量影响的大小与η大小成反比。为得到受冻融周期性波动影响的MR，首先应确定相应周期的η，然后乘以初次达到平衡含水率状态时的路基动回弹模量MR1。

通过分析室内动回弹模量实验结果，比对实验数据发现：进行曲线拟合时用幂函数的效果较佳，所有的R2>0.95，在接受范围之内。表5为回归分析结果。因此，不同状态下动回弹模量相对稳定值可通过回归分析而得到，同时基于此拟合曲线可计算出石灰改良土路基动回弹模量η值[9-13]。

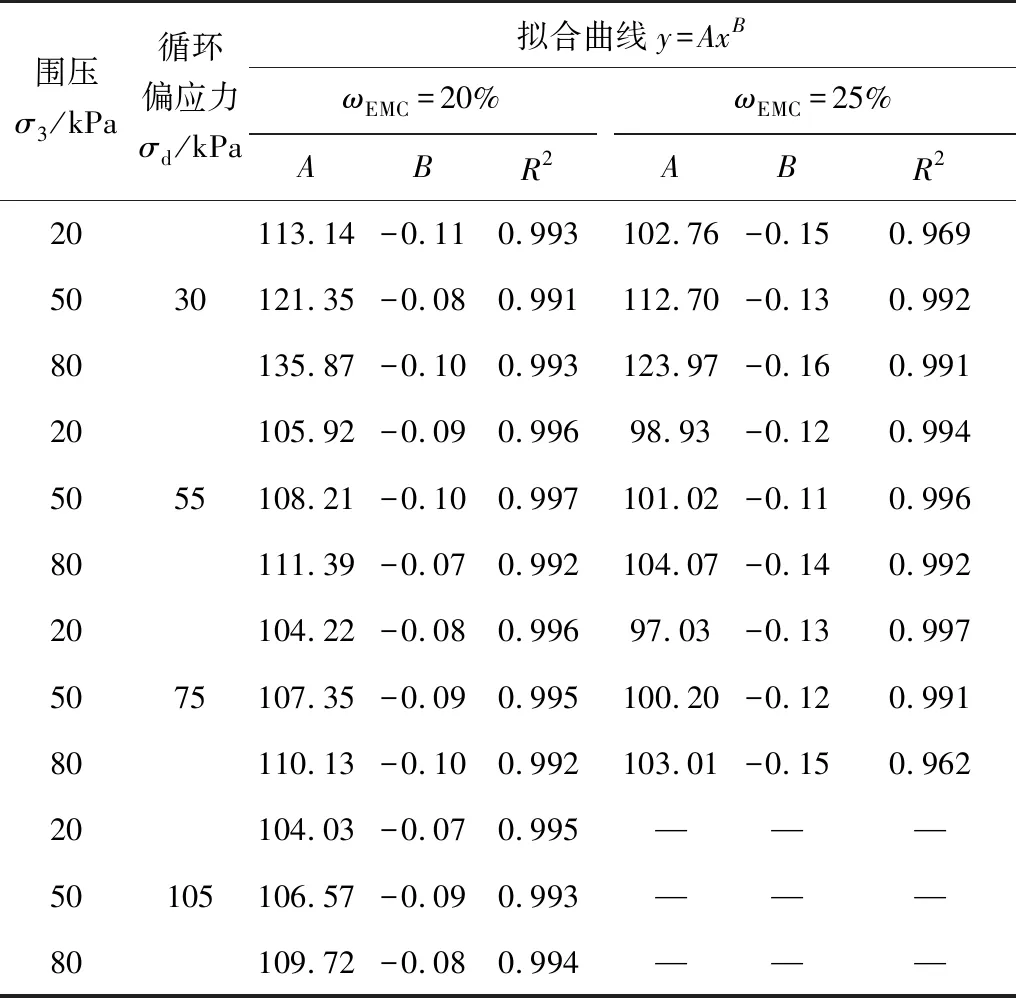
表5 动回弹模量实验结果拟合数据Table 5 Fitting data of dynamic resilient modulus test results

表6为石灰改良土路基动回弹模量冻融循环折减系数的计算结果。其中：MR1取N=1时的对应值，MR取N=8时的对应值。

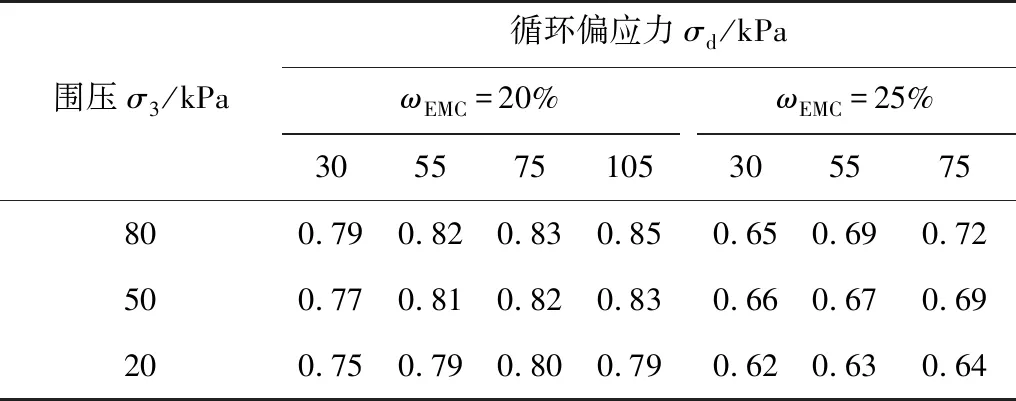
表6 动回弹模量冻融循环折减系数Table 6 Reduction coefficients of dynamic resilient modulus of freezing-thawing cycle

通过计算结果可知：在一般情况下，随着围压增大，冻融循环折减系数不断增大，说明可通过增大围压来降低冻融循环对石灰改良路基土动回弹模量影响；但对于较大EMC，当偏应力较低时出现了随围压增大折减系数η逐渐减小现象，即此状态下围压增大会产生负面影响。故此时应同时增大围压与偏应力才能有效降低冻融循环对石灰改良路基土动回弹模量影响。