基于试验的徐变模型修正及桥梁线型分析方法

2019-12-17毛江鸿曾甲华言建标

重庆交通大学学报(自然科学版) 2019年12期

毛江鸿，陆飞，张奕，曾甲华，言建标

(1. 重庆交通大学土木工程学院，重庆400074； 2. 浙江大学宁波理工学院，浙江宁波 315100； 3. 浙江省交通投资集团有限公司，浙江杭州 310014； 4. 中铁第四勘察设计院集团有限公司，湖北武汉 430000)

0 引言

徐变是混凝土材料本身固有的一种重要时变特性，是指混凝土在持续荷载作用下，结构的变形随时间不断增加的现象。徐变对混凝土结构的作用贯穿于结构施工至整个服役期，常导致大跨度预应力混凝土桥梁在长期运营后产生预应力损失、长期变形和内力重分布显著增加等问题[1-4]。随着混凝土结构向高强高性能化、结构形式多样化发展，工程界对于高强高性能混凝土材料徐变特性越来越重视。特别是对大跨径桥梁而言，对桥梁线形、下挠等方面具有严格控制要求，因此准确预测混凝土收缩徐变发展规律，对保障结构的长期性能至关重要。

目前国内外得到广泛认可并被实际工程普遍采用的模型主要有CEB-FIP系列模型、ACI 209R模型、B3/B4模型和JTG D62—2004模型等[5-8]。上述模型均是基于大量试验结果的回归拟合推导而出，不可避免地与实际情况存在差异，存在的差异即为收缩徐变模型的不确定性。准确预测徐变对桥梁施工阶段的线形控制以及运营阶段的维护极其重要，因此应对预测模型进行修正。Z. P. BAZANT等[9]指出通过混凝土收缩徐变试验，修正现行预测模型中的部分参数，可更真实反映结构收缩徐变长期效应；潘钻峰等[10-11]通过苏通大桥所用高强高性能混凝土的收缩徐变试验指出，CEB-FIP90模型不能准确预测其收缩徐变效应，提出修正模型并用于苏通大桥计算分析，结果表明预测值与实测值吻合；雷自学等[12]研究认为，对于重大桥梁工程的收缩徐变效应分析，需要开展混凝土收缩徐变试验和模型修正；B.DELSAUTE等[13]指出，精确的混凝土徐变预测模型必须基于早期的试验数据，并通过经典混凝土受压徐变试验来获取这一数据；韩伟威等[1]通过在恒温恒湿环境中，对5个圆柱形素混凝土柱进行受压徐变试验，将试验结果与常用模型进行对比分析，发现试验值和常用模型预测值会随着计算龄期增加其差异也逐渐增大。由此可见，常用的徐变预测模型并不能准确预测结果[14]，对于特定的桥梁，依据工程配合比进行专门的徐变试验，更能准确的预测实际结构的徐变发展情况。

笔者依托浙江温州乐清湾港区铁路支线瓯江特大桥，该桥为桥跨(52+90+300+90+52)m的大跨度铁路混凝土斜拉桥，其大跨度的特征使其更有必要开展徐变研究。为精确的预测徐变发展规律，在实验室试验的基础上，对桥梁整体建模分析其变形性能。

1 混凝土徐变试验及预测模型修正

1.1 混凝土徐变试验

1.1.1 试验概况

在前期理论分析及试验研究的基础上[15]，确定高性能混凝土的配合比，参数如表1，其中水胶比为0.318，矿粉与粉煤灰掺入均为11%，聚羧酸减水剂的掺量为1%，塌落度为200～220 mm。为验证该配合比下混凝土的力学性能指标是否符合铁路桥梁规范要求，测得混凝土抗压强度及弹性模量，如表2。

表1 C55混凝土基准配合比Table 1 Base mix ratio of C55 concrete kg/m3

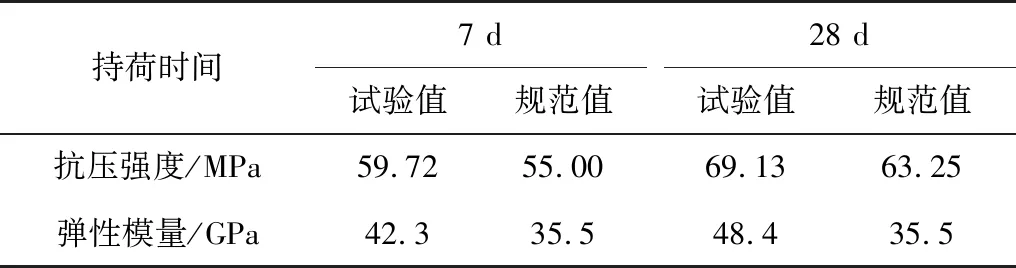
表2 C55混凝土力学性能Table 2 Mechanical properties of C55 concrete

笔者共制3组高性能混凝土试件，尺寸为150 mm×150 mm×550 mm棱柱体，编号C1～C3。其中C1、C2组用于受压徐变试验，每组制作2个；C3组用于自然收缩试验，制作3个，试验结果均为每组数据的平均值。试件采用外装式千分表变形测量装置，测量装置的两测头间距均为200 mm，千分表采用量程为0～5 mm的机械式千分表。根据GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》[16]，养护结束后移至恒温恒湿环境中。试件达到28 d龄期时放置于弹簧徐变仪装置上进行加载，持荷应力为所测得的棱柱体抗压强度的40%。

1.1.2 试验结果

对C1～C3组进行收缩徐变试验后，依据规范中的收缩徐变公式进行计算，分别计算收缩值与徐变值。

依据实际桥梁施工情况，同时为了方便与现有徐变预测模型进行对比。养护28 d后进行加载试验，并在实验室连续测量270 d的试验数据，其混凝土的收缩应变随时间发展曲线如图1。

图1 C55混凝土收缩应变曲线Fig. 1 Shrinkage strain curve of C55 concrete

混凝土的收缩应变在整个加载时程中存在一定波动，但从整体曲线来看，混凝土收缩应变随时间增加而增大。在收缩前期(约30 d内)收缩应变增加显著，该阶段混凝土收缩应变发展了全过程的46%，达到了90 με，大致呈幂函数增长。之后增加速率明显减缓，从第30 d到180 d增加了100 με，收缩应变呈低斜率的线性增长。在龄期180 d后，曲线发展极为缓慢，经历90 d时，收缩应变仅变化了10 με左右。

经公式计算，在考虑收缩应变的影响后，得到C55混凝土徐变应变，C1与C2组的徐变应变曲线与C3组的收缩应变曲线走势基本保持一致，如图2。虽两条曲线之间存在一定差异，但整体上吻合度较高。

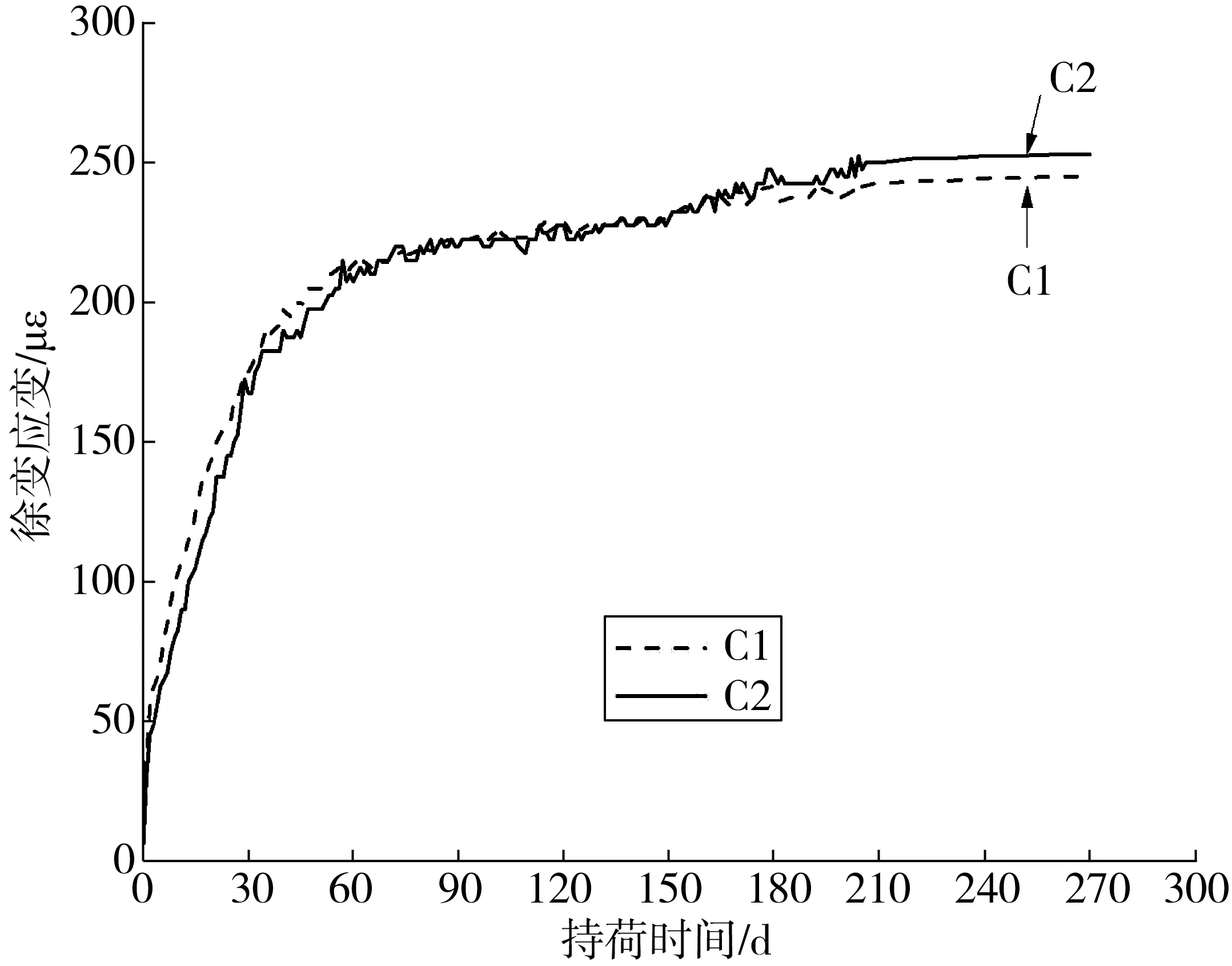
图2 C55混凝土徐变应变曲线Fig. 2 Creep strain curve of C55 concrete

对图2中两条曲线进行拟合，将拟合结果作为最终的试验数据，并通过计算可得到C55混凝土徐变度随时间发展曲线，将之与文献[17]和[18]中的试验数据进行对比，如图3。发现即使高性能混凝土的强度相似，但混凝土徐变与其配合比密切相关[19]。总体来看，笔者数据与其他学者试验结果相近。

图3 各文献中高性能混凝土徐变度对比Fig. 3 Comparison of creep degree of high performance concrete in each literature

1.2 徐变预测模型对比

将图3中拟合的试验数据(实测值)与各国规范中徐变预测模型生成的预测值(规范值)进行对比分析，如图4。

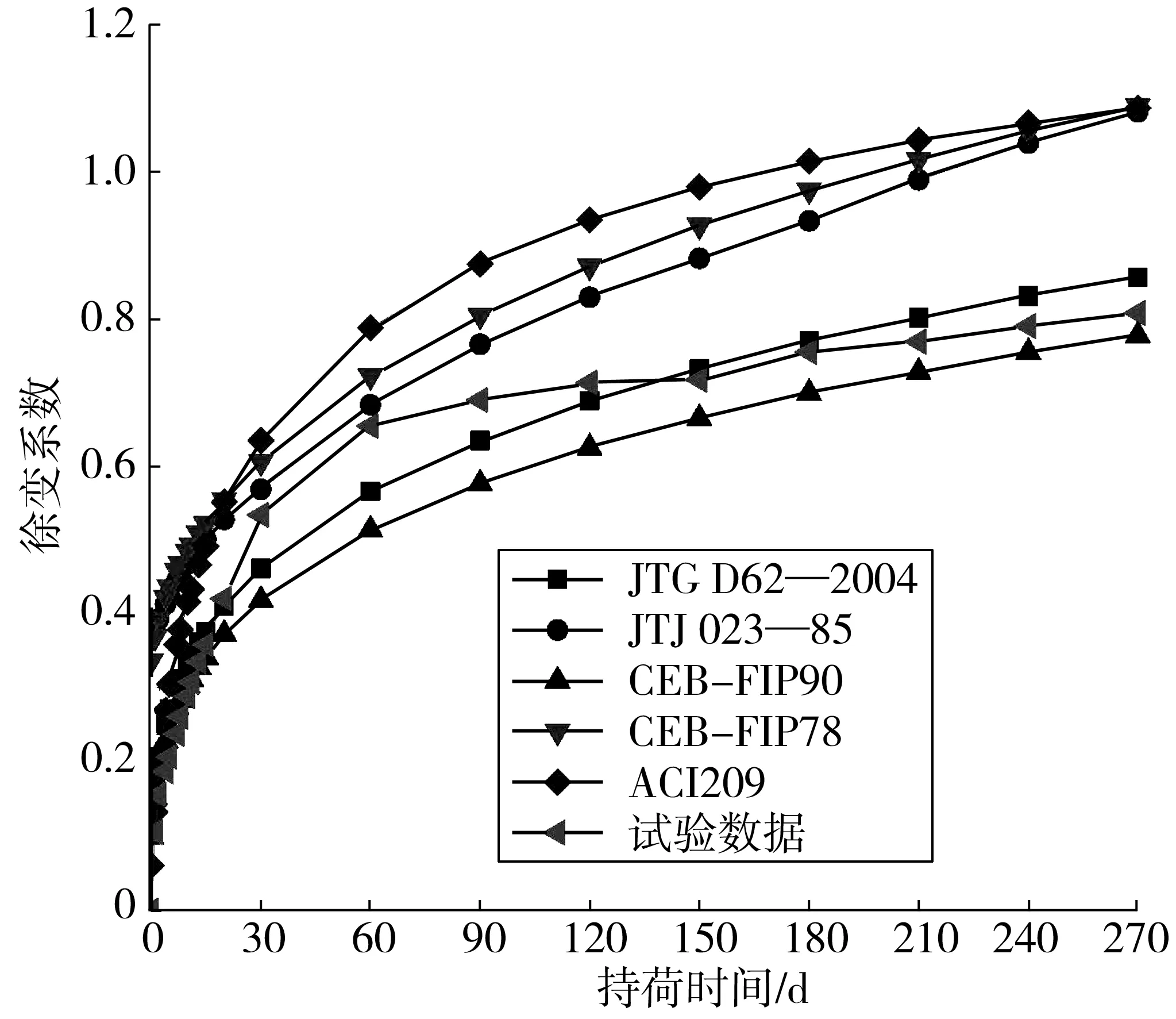
图4 C55混凝土徐变系数实测值与规范值对比Fig. 4 Comparison of the measured and the speculated values of C55 concrete creep coefficients

由图4分析可知，试验数据与各规范值存在较大差异，这是由于各规范值是基于其他试验结果的回归拟合推导出，与本次试验实际情况存在差异，即为收缩徐变模型的不确定性。同时发现，早期的徐变预测模型如JTJ 023—85和CEB-FIP78模型，因未能精确的考虑徐变影响因素，导致规范值明显高估了混凝土的收缩徐变。当前常用的JTG D62—2004和CEB-FIP90模型的规范值与实测值较为接近，但在120d前低估了徐变发展。ACI209模型则是在整个时程中均高估混凝土的收缩作用，导致其预测值远大于实测值。在文献[11]中也得到笔者相似结论，由此表明选用不同的徐变预测模型存在差异。

1.3 基于试验的徐变预测模型修正

混凝土在长期常荷载作用下徐变可延续30年以上，而室内徐变试验因条件限制无法长时间测量，一般持续荷载时间为1～2年，有些试验持荷时间仅有几个月。由于试验场地的限制，笔者持荷时间为270 d。此情况下须从短期试验资料预测长期徐变，为实际工程提供指导。基于文献[20]的徐变预测经验式(B&N经验式)，如式(1)。结合笔者试验数据进行拟合修正，得到适用于笔者C55混凝土的长期徐变预测模型(下简称修正式)，如式(2)。

B&N经验式：

CTt=CT28(2.15lnt-6.19)1/2.64

(1)

修正式：

CTt=CT28(1.71lnt-5.31)1/3.36

(2)

式中：CTt为加荷td的混凝土总徐变预测值，CT28为加荷28 d的混凝土总徐变试验值。

文献[19]指出，若持荷时间少于120 d，则误差系数超过10%；若持荷时间大于1年，则误差系数小于5%，增加短期试验时间，可以提高预报精度。笔者的持荷时间选为270 d，其误差系数较为合理。

将修正式曲线与原始试验数据、B & N经验式、直接拟合曲线进行对比分析，如图5。

图5 混凝土徐变预测模型修正及对比Fig. 5 Correction and comparison of concrete creep prediction model

由图5可知，若直接采用B & N经验式，因配合比原因预测结果与实际情况误差较大；若直接对试验数据进行曲线拟合，其表达式见式(3)：

CTt=3.741 5ln(t)-0.163 7

(3)

该曲线为对数函数，与实际的幂指数函数不符，预测结果误差会随持荷时间的增加而增大。此外，修正式在29～120 d内误差较大，但在120 d后曲线拟合度较高，可用于后期的徐变预测。通过计算可知10年内的徐变度随时间发展曲线如图6，其中，270 d内的数据为实测值。

图6 10年内徐变度随时间发展曲线Fig. 6 Curve of creep degree changing with time within 10 years

为验证持荷时间对预测精度的影响，笔者分别对持荷时间为60、90、120、150、180、210、240 d的试验数据进行分析，将对应上述持荷时间的预测曲线与270 d的试验数据进行对比，结果如图7。

图7 基于不同时间区间的预测精度对比Fig. 7 Comparison of prediction accuracy based on different time intervals

图7中曲线由上至下分别表示在持荷时间60～240 d后，基于该时间区间来预测混凝土的长期徐变曲线，可以看出若采用较短持荷时间数据进行预测，后期的误差会更明显。

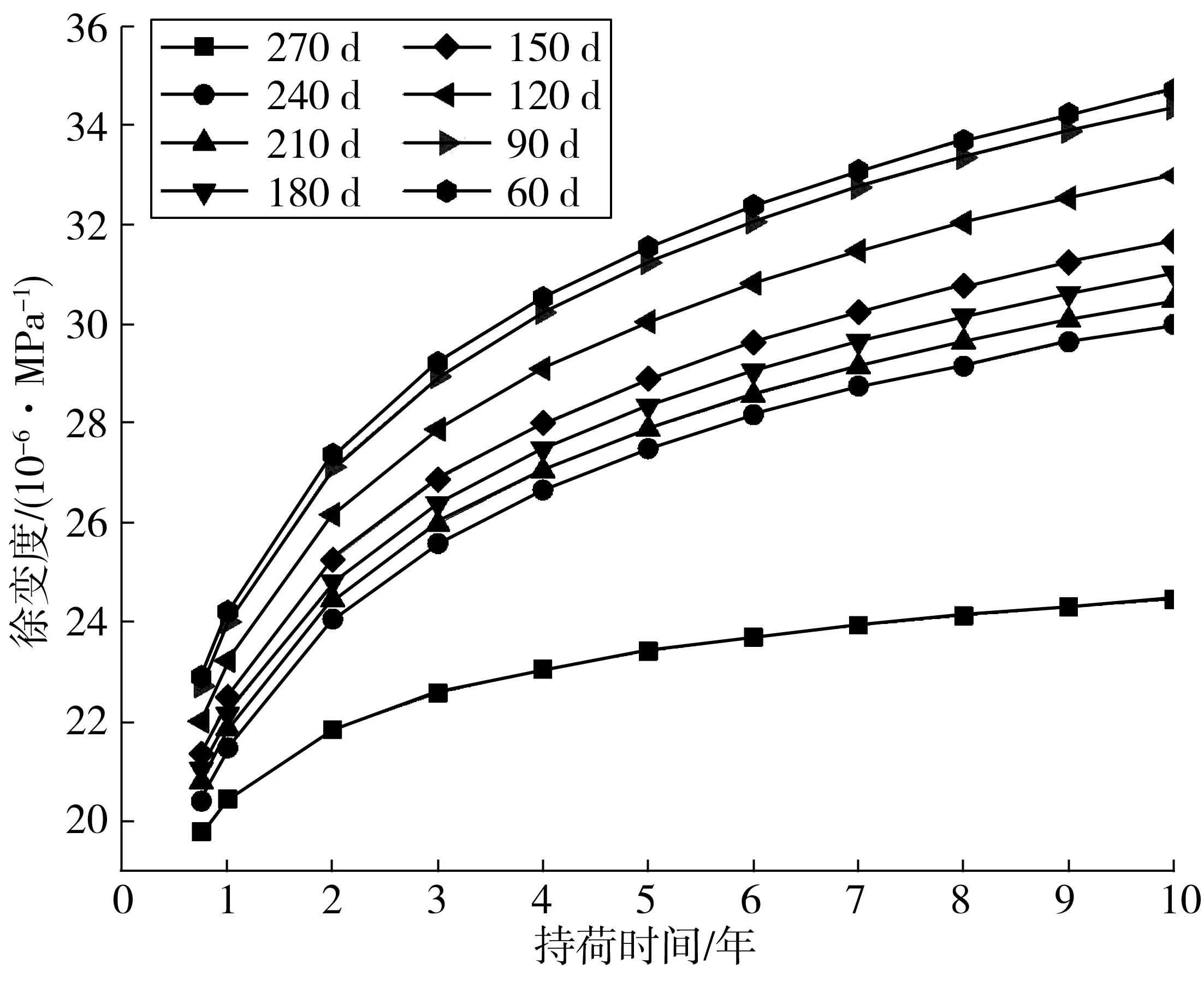
图8 10年内各预测曲线徐变度对比Fig. 8 Comparison of creep degree of prediction curves within 10 years

为观察较长时间内的差异，将上述预测曲线发展10年内的徐变度终值进行对比，如图8。在第270 d，各曲线徐变度预测值最大偏差(最大值与最小值的差值所占百分百)为26%；在第10年，各曲线徐变度最大偏差达到了42%。结果表明：基于不同持荷时间内的实验室数据进行长期的徐变预测，预测差异会随着时间的增加而不断增大。

研究发现混凝土徐变预测模型会由于试验设计的配合比、持荷时间等影响会导致预测结果产生差异，通过室内试验并依据实验室数据进行预测模型修正可提高预测精度。

2 短期及长期变形分析

依据瓯江特大桥的相关设计图纸，使用Midascivil对其建立全仿真模型，如图9。软件中考虑混凝土徐变，通过在“材料”属性界面添加一种随时间变化的特性，而不是常规意义上的荷载作用。笔者仅考虑混凝土徐变作用，分析该桥在徐变作用下主梁的变形。为了直观观察主梁的变形，仅对两索塔之间的主跨进行数据分析。

图9 瓯江特大桥模拟模型Fig. 9 Simulation model of Oujiang uper-long Bridge

2.1 短期变形性能分析

笔者依据270 d内的实验室数据来预测实际桥梁在短时间的变形性能，并将其与采用规范值计算得到的主跨竖向位移进行对比，如图10、表3。

图10 不同规范下主跨竖向位移Fig. 10 Vertical displacement of main span under different specifications

表3 采用不同规范下主跨竖向位移具体数值Table 3 Specific numerical values of vertical displacement of main span under different specifications

从图10可以看到，选用不同规范中的徐变预测模型均导致其计算结果高估了桥梁的变形性能，但整体趋势基本一致。采用实验室数据模拟的结果与采用JTG D62—2004规范和CEB-FIP90规范模拟计算的结果较为接近。由表3可知，采用实验室数据模拟得到主跨跨中最大竖向位移为15.362 cm，与采用CEB-FIP90规范偏差值最小为6.4%，即竖向位移最大偏差0.984 cm；采用CEB-FIP78规范偏差值最大为69.9%，即竖向位移最大偏差达到10.738 cm。

2.2 实桥长期变形性能分析

将采用试验修正模型预测值计算后桥梁在不同运营阶段其主跨竖向位移作对比，结果如图11。

图11 主跨竖向位移的长期变化趋势Fig. 11 Long-term change trend of vertical displacement of main span

由图11可知，随持荷时间的增加，主跨跨中变形不断增大，但增长的趋势显著变缓。成桥后第1年里，其跨中竖向位移从16.574 cm增长到19.623 cm，变化了3.049 cm；但在第7～10年间，从26.989 cm增长到27.785 cm，仅变化了0.796 cm。

将不同运营阶段内的试验修正模型的预测值与规范值计算得到的主跨跨中竖向位移进行对比，如图12。

图12 不同规范长期主跨跨中竖向位移对比Fig. 12 Comparison of mid-span vertical displacement of long-term main span in different specifications

由图12可知，经试验修正模型预测值与规范值计算后的主跨跨中变形值会随着运营阶段时间的增加而不断增大。在第5年时，修正模型与CEB-FIP模型模拟后差值为1.373 cm，到第10年差值则增大到1.909 cm；若采用我国旧规范JTJ 023—85对实际桥梁进行模拟预测，其10年后的预测值与采用笔者方法计算后的数值差异达到19.501 cm。由此可发现采用不同徐变预测模型对计算结果的差异性较大，对于实际工程应用，若使用笔者方法进行模拟计算，这对新建桥梁设置预拱度有较大的指导意义。