基于自适应控制的非线性多智能体系统一致性
2019-12-17唐朝君
唐朝君
(重庆理工大学 理学院, 重庆 400054)
由于当前多智能体系统在分布式传感器网络、编队控制、信息融合和蜂拥等问题中的广泛应用,对多智能体系统的研究吸引了不同领域研究学者的广泛关注。一致性是多智能体系统协调控制研究的基础,也是多智能体系统研究中最重要和最基本的一个问题。一致性是指通过设计恰当的分布式控制协议,使系统中的智能体就某些关键的量趋于一致。根据系统中是否有领导智能体,可以将一致性分为两类,即无领导的一致性和领导跟随一致性。
1995年,Vicsek等[1]提出了一个简单却十分有趣的离散时间多智能体系统模型,通过仿真演示了系统中所有的智能体最终以共同的方向前进。2003年,Jadbabaie等[2]利用矩阵理论和代数图论的方法首次给出了Vicsek模型的理论解释。Olfati-Saber和Murray[3]对连续时间多智能体系统的一致性研究做了开创性的工作,分别研究了固定和切换网络拓扑下的一致性问题,以及带有单一时滞的一致性问题。随后,Ren等[4]研究了更为一般的网络拓扑,给出了系统解决一致性所需的最弱的拓扑条件。随着一致性问题研究的不断深入,发展了一系列的重要的子课题,主要包括具有通信时滞的一致性、带有测量噪声的一致性、有限时间一致性、基于时间触发机制的一致性和随机网络拓扑下的一致性问题等,具体参见文献[5]。
在实际应用中,绝大多数的物理系统本质上都是非线性系统。因此,对非线性多智能体系统一致性的研究具有重要意义。近年来,对非线性多智能体系统一致性的研究得到了一些有趣的结果。受同步理论的启发,文献[6-7]在一致性协议中引入了非线性函数来描述智能体内在的非线性动态。针对有向网络拓扑,提出了广义代数连通度的概念,并用其得到了一致性的充分条件。文献[8-9]利用牵制控制(pinning control)研究了二阶非线性多智能体系统的领导-跟随一致性问题。文献[10]研究了非线性多智能体系统的有限时间一致性问题。文献[11]研究了非线性多智能体系统的包含控制问题。
在现有大多数对一致性问题研究的文献中, 所给出的一致性协议中都需要用到网络拓扑所对应的Laplacian 矩阵特征值的信息, 这是一个全局的信息,因此这些控制协议并非严格意义的分布式控制协议。为了解决这个问题,一些研究学者提出了基于自适应的控制协议。目前,对基于自适应控制协议的一致性的研究已经得到了一些有趣结果[12-15]。另外,文献[6-11]中都是假设系统中的智能体具有相同的非线性动态,而对具有不同本质非线性动态多智能体系统一致性的研究还鲜有报道。基于非线性动态的参数化分解,Yu等[16]对具有不同本质非线性动态多智能体系统提出了一种基于自适应的控制协议来追踪同样具有未知非线性动态的领导智能体。受文献[16]的启发,本文研究具有不同本质非线性动态多智能体系统的一致性问题。与文献[16]相比,本文的创新之处主要体现在两个方面:① 本文研究的是无领导的一致性问题,适用于更为一般的多智能体系统;② 文献[16]只研究了无向网络拓扑,本文分别研究了无向和有向网络拓扑。值得注意的是,有向网络拓扑更加符合实际应用,而无向网络拓扑可视为有向网络拓扑的特例。
1 问题描述
考虑由n个智能体构成的多智能体系统。智能体i的动力学模型为
(1)
式中:xi∈R是智能体i的状态;ui(t)∈R是智能体i的控制输入;fi(xi,t)∈R是智能体i自身动力学的非线性函数。
假设非线性函数fi(xi,t)满足如下Lipschitz条件:
|fi(xi,t)-fi(xj,t)|≤l|xi-xj|
(2)
式中:xi,xj∈R;l>0为正常数。上述条件用于保证系统(1)解的存在性和唯一性。本文研究具有不同非线性动态的多智能体系统一致性问题,即对每个智能体设计分布式的控制协议ui,使所有智能体的状态趋于一致。具体问题由如下定义给出:
定义1若系统(1)的解在任意初始条件下满足
则称多智能体系统(1)解决一致性问题。
本文利用有向图来描述系统中智能体之间的拓扑结构。有向图G由一个顶点集V和边集E组成,其中V={1,2,…,n},顶点i表示智能体i,E={(i,j)|i,j∈V}。若智能体i能接收到智能体j的信息,则(j,i)∈E,否则(j,i)∉E。若(j,i)∈E, 则称顶点j是顶点i的邻居或者智能体j是智能体i的邻居。从vi1到vik的一条路径是由一系列不同的顶点vi1,vi2,…,vik构成,并且这些顶点满足(vij,vij+1)∈E,j=1,2,…,k-1。如果从G中任一顶点到另外一顶点都有路径存在,则称G是强连通的;如果G中至少有一个顶点到其他顶点都有路径存在,则称G包含生成树。对于有向图G,如果(i,j)∈E蕴含着(j,i)∈E,那么称G是无向图;若无向图G包含生成树,则称G是连通的。

图G的Laplacian矩阵L=[lij]∈Rn×n定义为

Laplacian矩阵在一致性问题的研究中具有非常重要的作用, 它具有下面的性质[4]:
引理1 0是L的特征值, 1n=(1,1,…,1)T∈Rn是对应的特征向量,其他非零特征值的实部全部大于0;0是L代数简单的特征值当且仅当图G包含生成树。
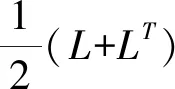
2 主要结果
本节给出分布式的控制协议,使系统(1)能解决一致性问题。假设非线性动态fi(xi,t)可进行线性参数化:
式中:φi(xi,t)∈Rm为已知的基函数向量,θi∈Rm为未知的常数参数向量。
注1本文假设智能体的非线性动态可以进行线性参数化。线性参数化的模型在经典的自适应控制中已经被广泛研究[17-18]。文献[16,19-21]对线性参数化的多智能体系统进行了研究。
使用如下的分布式控制协议:
(3)
首先研究固定拓扑的情形,此时系统的通信拓扑保持不变。利用协议(3),系统(1)可以写成下面的向量形式:
(4)
定理1假设系统的通信拓扑G连通。利用协议(3), 系统(1)解决一致性问题。
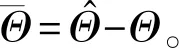
则


G是连通的无向图,则L是对称阵,而且存在正交阵U=(u1,u2,…,un)∈Rn×n,使得
UTLU=diag{λ1,λ2,…,λn}

eTLe=eTUdiag{λ1,λ2,…,λn}UTe=

对于有向网络拓扑, 容易得到下面的结论:
定理2假设系统的通信拓扑G是平衡图且包含生成树。利用协议(3),系统(1)解决一致性问题。
证明使用定理1证明中的记号。注意到
由于G是平衡图且包含生成树, 由引理2可得
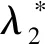
在实际应用中,由于障碍物的存在或者个体之间的相互影响,系统中的通信拓扑往往是时变的,因此研究时变拓扑下的一致性问题更具有实际意义。设P={G1,G2,…,Gs}为系统所有可能通信拓扑的集合, 其中m<+∞。为了描述时变拓扑, 定义分段定常切换信号:σ(t):[0,+∞)→J={1,2,…,s}。因此, 时刻t时系统的通信拓扑为Gσ(t),简记为Gσ。此时,系统(4)变为
(5)
定理3假设系统的通信拓扑Gi,∀i∈J连通。利用协议(3),系统(1)解决一致性问题。
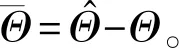
与定理1的证明方法相同,可得
注意到Gσ为连通的无向图,可得
eTLσe≥λ2(Lσ)eTe

3 数值模拟
本小节给出2个实例来验证本文理论结果的正确性。考虑1个含有5个智能体的多智能体系统,智能体i的非线性动态可以参数化为
fi(xi,t)=[xisint,xicost]θi,i=1,2,…,5


例1设系统的通信拓扑如图1所示。为方便起见, 设图中每条边的权值均为1。智能体的初始位置随机地选取为x(0)=(2,1,3,5,8)T和x(0)=(1,5,2,4,3)T,在协议(3)的作用下,智能体的状态随时间的变化曲线如图2、3所示。显然,智能体的状态随着时间的变化趋于一致,与定理1的结论相符。

图1 系统的通信拓扑G1

图2 智能体的状态曲线1
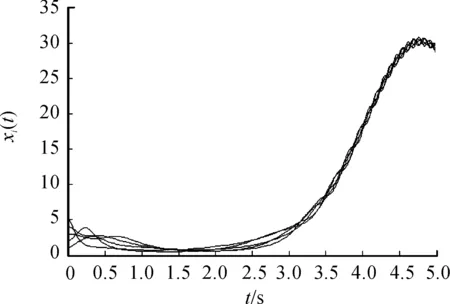
图3 智能体的状态曲线2
例2设系统的通信拓扑如图4所示。为方便起见, 设图中每条边的权值均为1。显然G2是平衡图且包含生成树。智能体的初始位置随机地选取为x(0)=(2,1,3,5,8)T和x(0)=(1,5,2,4,3)T。在协议(3)的作用下,智能体的状态随时间的变化曲线如图5、6所示。显然,智能体的状态随着时间的变化趋于一致,与定理2的结论相符。

图4 系统的通信拓扑G2
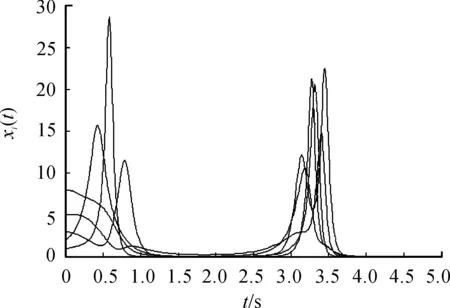
图5 智能体的状态曲线3
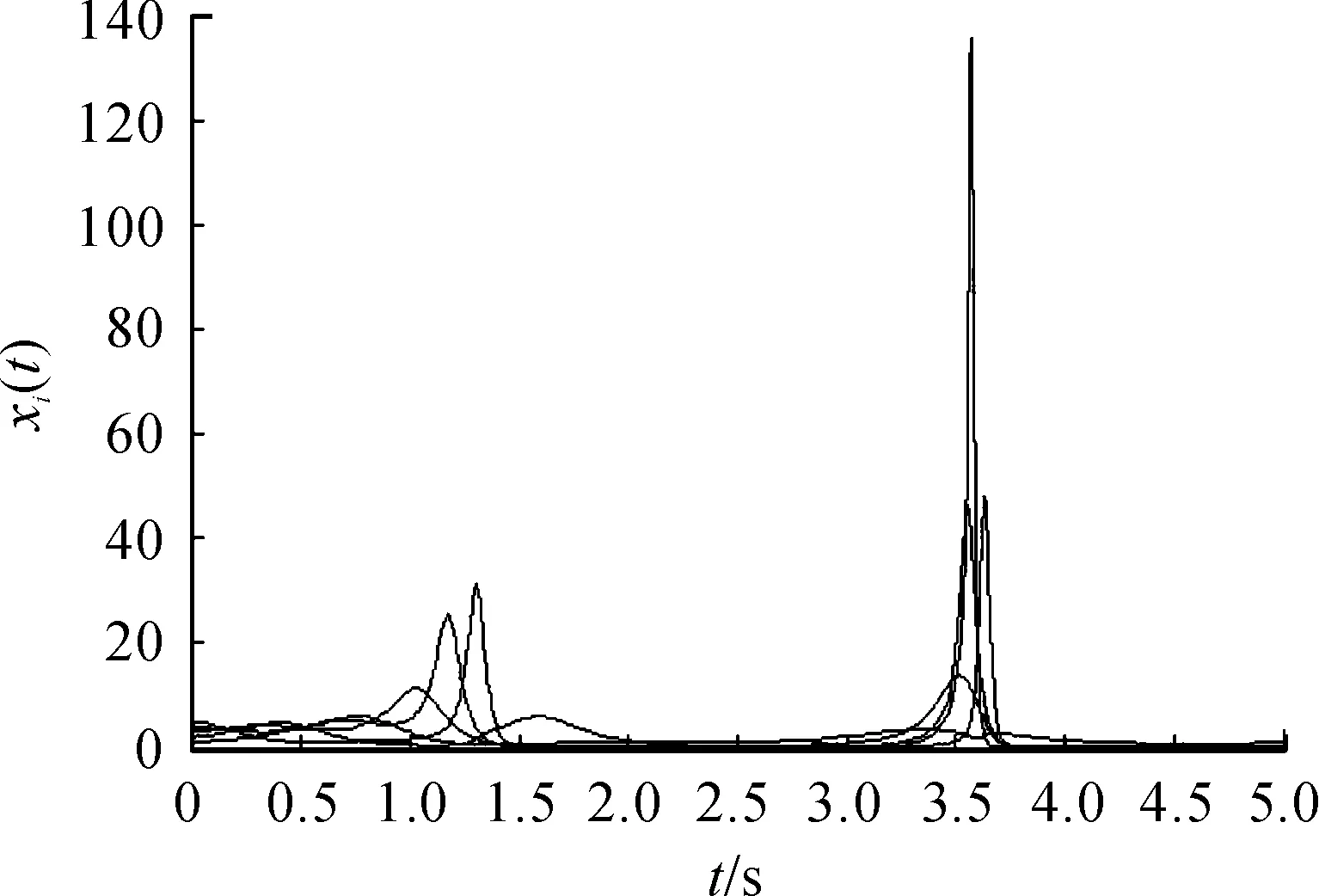
图6 智能体的状态曲线4
4 结束语
针对具有未知和不同非线性动态的多智能体系统,基于非线性动态的线性参数化分解的方法,给出了基于自适应的一致性控制协议。利用代数图论、矩阵理论和Lyapunov的方法进行稳定性分析。对于无向拓扑,当通信拓扑连通时,所给的协议解决一致性问题;对于有向拓扑,当系统的通信拓扑是平衡图且包含生成树时,所给的协议解决一致性问题;对于切换网络拓扑,当系统所有可能的通信拓扑连通时,所给的协议解决一致性问题。最后通过仿真实例验证了理论结果的正确性和有效性。
