智能车队跟车纵向控制算法设计及仿真验证

叶 心,魏劲鹏,杨杰星, 叶 明, 吕 强

(1.重庆理工大学 a.车辆工程学院；b.汽车零部件先进制造技术教育部重点实验室，重庆 400054；2.重庆美万新能源汽车科技有限公司，重庆 401121)

智能汽车是一个集外部环境感知、行驶路径决策、车辆辅助控制等功能于一体的综合系统，车辆的纵向控制技术是智能汽车最终“落地”的关键技术之一，目前已成为汽车领域研究的热点及重点。将车辆纵向控制技术应用到智能车队自动驾驶上，在缓解道路拥堵、保证交通安全以及驾驶节能等方面有重要意义[1]。

车辆纵向控制算法是连接上层跟车决策层和下层车辆执行机构的桥梁。上层控制器以车路相对位置为参照，规划车辆的期望运动状态，如驾驶人模型[2-3]和人工势场法[4-5]；下层控制器利用上层控制器的输出设计车辆控制器，如LEE等[6]应用参数自整定模糊PID控制，通过模糊规则对PID的3个参数进行调节，实现汽车纵向控制。Hedrick等[7]提出三状态模型，忽略发动机动态特性、液力变矩器特性、轮胎滑移，以进气量、发动机转速和制动力矩3个状态进行车辆控制。部分学者采用直接式控制方式[8]和分层式控制方式[9-10]，建立并开发了参数自适应型速度控制策略,适用于强鲁棒性控制系统，但未考虑车辆队列行驶时的应用。在车辆队列控制方面，张向南等[11-13]研究了车辆队列纵向控制的基本理论、控制方法和实验手段，未考虑领航车模型，但为车辆队列系统控制提供理论基础和技术支撑。

本文将车辆纵向动力学建模方法、模糊智能控制应用在车队纵向跟车控制中，建立包括领航车模型、车队纵向动力学模型、跟车模型等，为达到提高车队通行效率以及安全行驶的目的，保证车队车辆速度差小于5 km/h，车车间距差值波动率在靠近时小于20%，远离时小于30%，最后通过仿真分析，验证模型和控制器的性能和可行性。

1 领航车纵向动力学模型及仿真分析

领航车是车队中位于首位的车辆，并按照给定的城市循环工况ECE中规定的车速、加速度以及减速度的指令行驶。本节首先建立领航车纵向动力学建模，包括驾驶员模型、发动机模型、变速器模型、换挡模型、制动系统模型以及整车驱动模型，这些模型在建立过程中进行了如下假设：

1) 假设在路况良好的平路上行驶，无坡度；

2) 汽车轮胎与地面有良好的接触，并且地面有充足的附着力，不存在轮胎相对地面滑移之类的非线性因数；

3) 发动机的工作状态为理想工作状态下的瞬态修正。

与真实的道路情况相比，ECE只对道路车速、加减速、红绿灯等因素进行了理想的模拟，考虑真实的道路存在打滑、弯道以及通讯延迟等实际情况，为了避免车辆队列行驶时出现安全隐患，在车间距保持方面引入安全系数ζ。

1.1 研究对象

车队中的车辆全部为国产某车厂的同一款前置前驱AMT轿车，其整车及动力系统参数如表1所示。

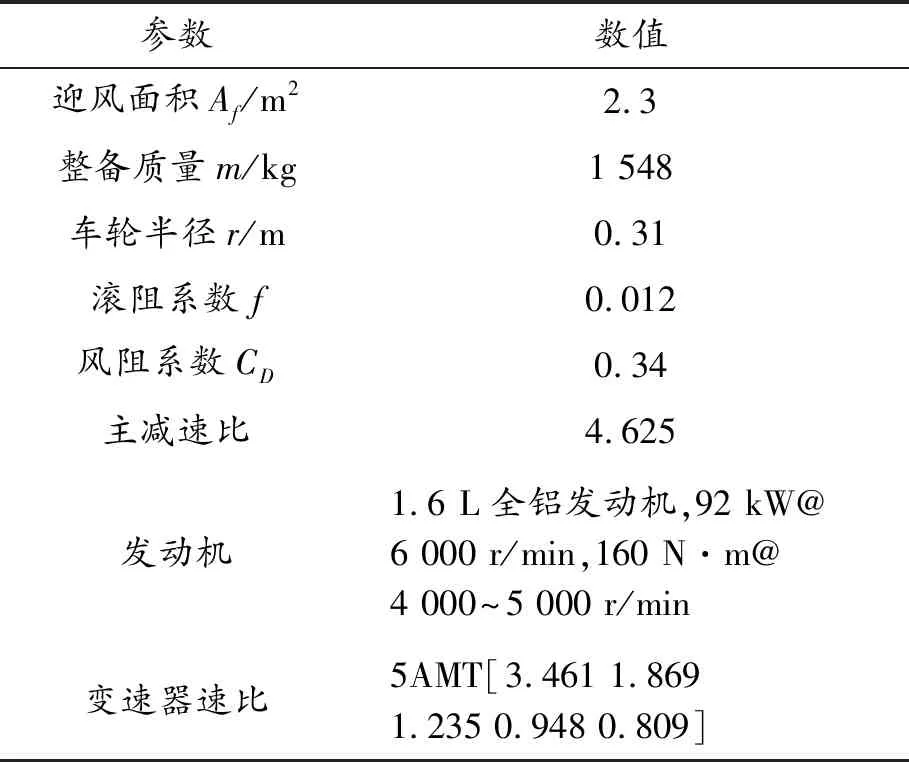
表1 整车及动力系统参数

1.2 领航车纵向动力学模型

领航车的纵向动力学模型，包括驾驶员模型、发动机模型、变速器模型、驱动桥模型(主减速器、差速器)以及制动系统模型5个部分，基于车辆动力学领域的研究成果以及经验数据，各个部分通过力矩、转速的传递关系连接，建立单个车辆整车纵向动力学模型，如图1所示。

1) 驾驶员模型

驾驶员模型提供整车模型的输入信号，包括油门踏板开度以及制动踏板开度。为了使驾驶员模型接近真实的情况，采用具有强鲁棒性的模糊逻辑智能算法，通过对比实际车速与期望车速的差值，以及该差值的变化率，将车速需求转化为油门踏板或者制动踏板的开度，建立驾驶员模型，如图2所示。

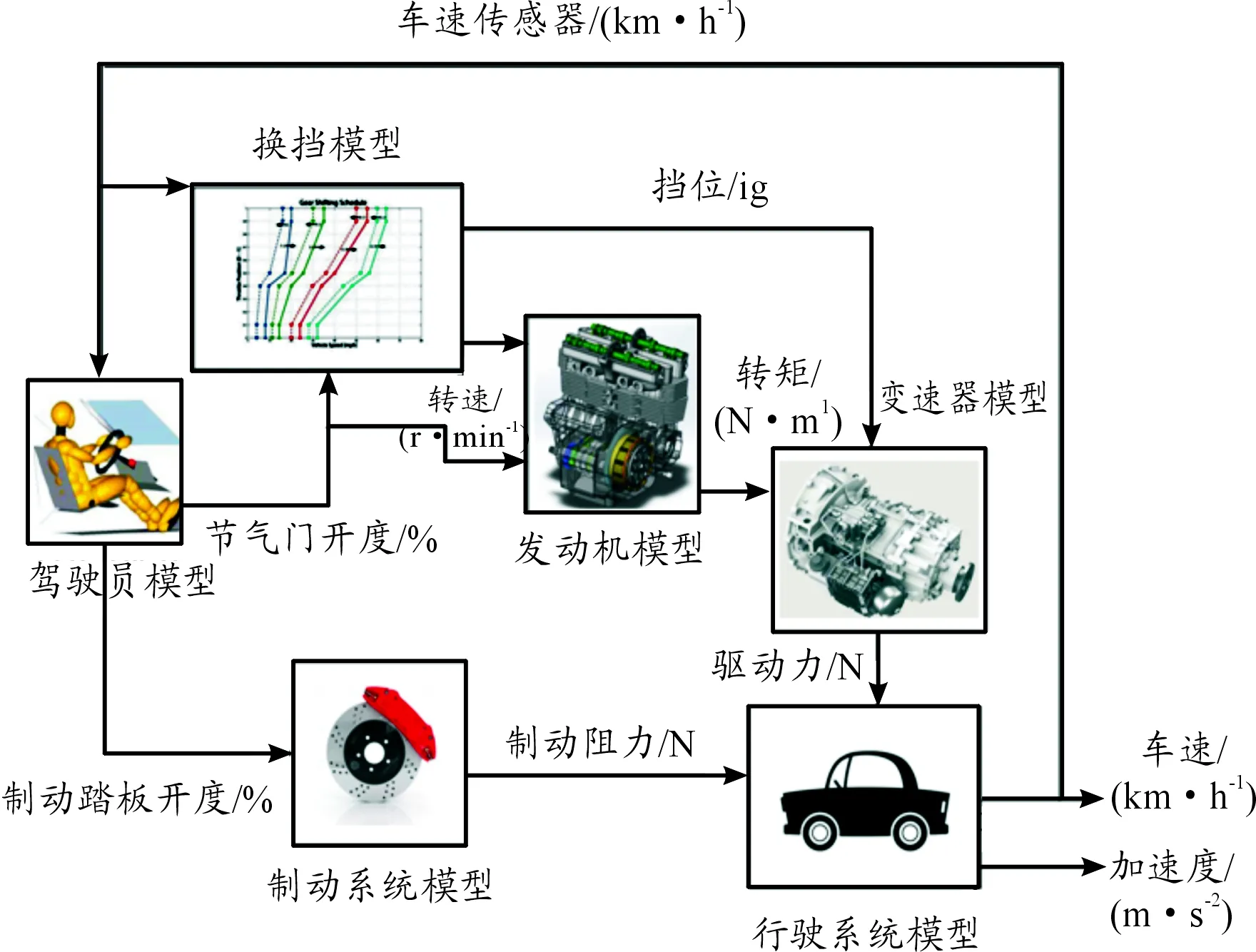
图1 领航车纵向动力学系统模型

2) 发动机模型

由于发动机有动态工作负载，导致其常处于一种不稳定的运行工况中。本文采用发动机稳态数据拟合并动态修正的方法来建立发动机模型。根据内燃机的工作原理可知，发动机所输出的转矩与曲轴的转角、进入汽缸的混合气体质量、空燃比以及其他因素有关，在进行发动机系统动态建模过程中，基于发动机稳态实验数据，通过动态修正，搭建1阶惰性发动机模型来补偿动态误差，如式(1)所示。

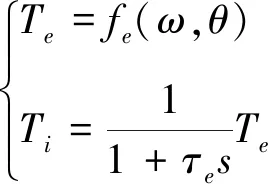
(1)

式中:Te为理想的发动机输出转矩(N·m)；θ为油门的开度；ω为发动曲轴转速(r/min)；τe为发动机扭矩阶跃响应时间常数；Ti为发动机实际输出扭矩(N·m)。

3) 变速器模型

本文研究对象为5挡AMT自动变速器，可根据当前车速和节气门开度选择合适挡位。变速器输入轴与发动机输出轴通过离合器连接起来，起到减速增矩的作用，因此自动变速器的输出轴扭矩Tg及转速ng计算如式(2)所示。

(2)

式中ig为当前挡位传动比。

基于式(2)及AMT综合性换挡规律，在Matlab/Simulink/Stateflow仿真平台搭建变速器换挡模型，如图3所示。

图2 领航车驾驶员模型

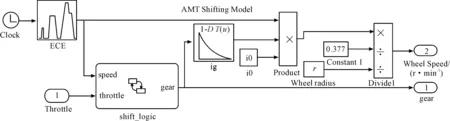
图3 AMT换挡模型

4) 制动系统模型

制动系统模型是确保车辆按照预期的车速行驶，以及与前车保持安全距离的重要手段。驾驶员制动意图可通过制动踏板力与期望制动减速度关系来表示，制动踏板力与期望制动减速度之间的关系如式(3)所示。

(3)

式中：Fb为估算出的制动踏板力(N);Pm、Am分别为人力制动主缸的压力(Pa)及活塞有效面积(m2)；Ks为弹簧刚度(N·m-1);Rpedal为制动踏板杠杆比;Pb为制动踏板位移(m)，一般可以通过实车场地实验的数据拟合等获得。

5) 车辆行驶系统模型

假定车辆在良好路面行驶，且只考虑汽车的纵向受力情况，汽车行驶系统承受来自传动系统输出的转矩转化的驱动力Fx、空气阻力Fw、滚动阻力Ff、加速阻力Fj以及制动阻力Fb，汽车受力平衡如图4所示。

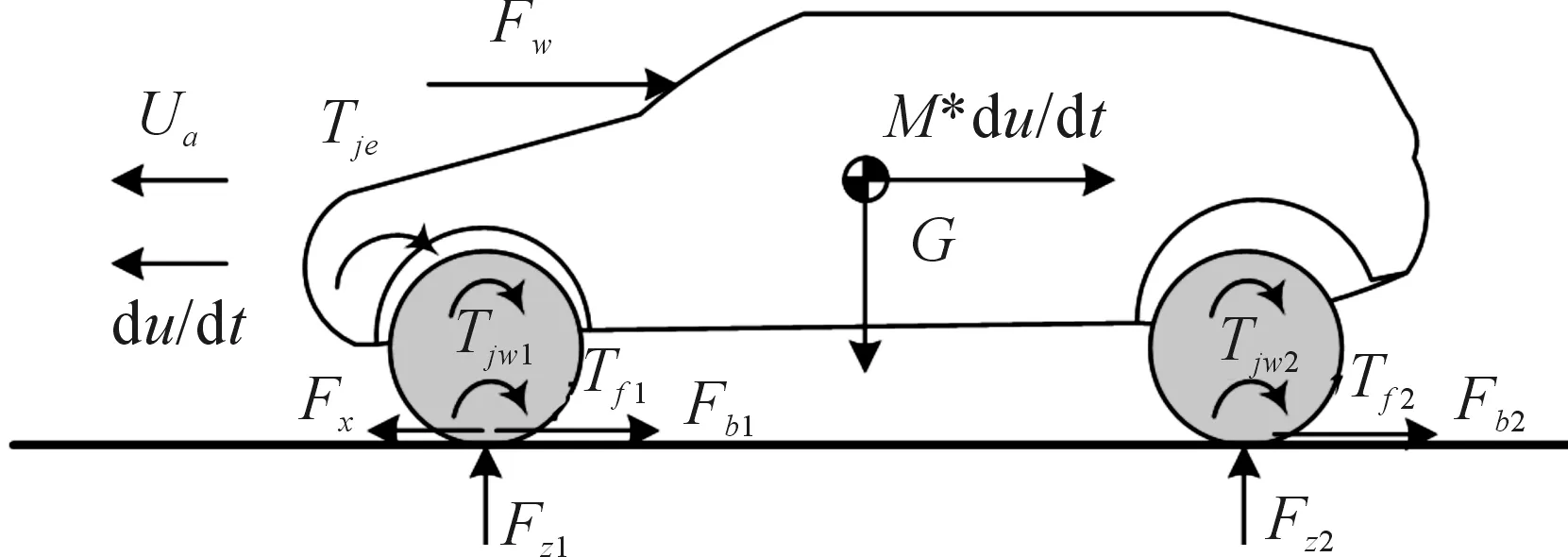
图4 汽车受力平衡图

根据图4，得到汽车在行进过程中的受力平衡方程式：

Fx=Fw+Ff+Fb+Fj

(4)

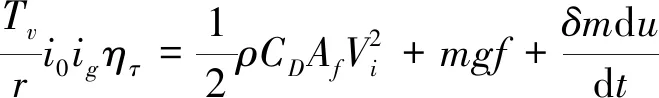
(5)

式中：δ为汽车的旋转质量转换系数(根据经验数据δ>1，且在1.1～1.4之间，本文研究对象为C级轿车，故δ=1.3)；ρ为空气密度(g/cm3)；CD为空气阻力系数；Af为迎风面积(m2)；Vi为第i辆车的纵向速度(km/h)，忽略风速；Td为车轮处驱动转矩(N·m)；Te为发动机飞轮处输出转矩(N·m)；m为汽车质量(kg)；f为道路摩擦因数；du/dt为车辆纵向加速度(m/s2)；r为车轮半径(m)；i0为主减速器传动比；ig为变速器当前工作档位速比；ητ为传动系传动效率。

1.3 领航车驾驶模型仿真分析

基于Matlab/Simulink/Stateflow仿真平台，对上述小节中的领航车模型进行仿真分析，以ECE道路循环工况为目标车速，仿真结果如图5所示。

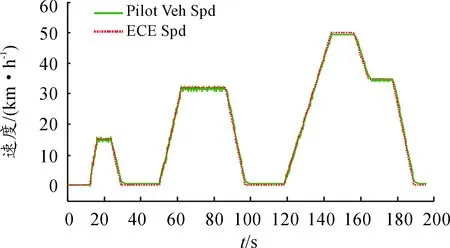
图5 领航车行驶车速与ECE车速对比

图5中，虚线为ECE道路循环工况目标车速，实线为领航车的实际车速。通过仿真结果可知，领航车行驶车速与ECE循环工况的车速最大差值不超过2 km/h，较好地实现了领航车按照预定的车速，加速、减速行驶要求的目的。

2 智能车队跟随控制器设计及仿真分析

车辆的队列行驶是指2辆以上的汽车，在以相同的车速行驶的基础上，两两车辆之间按相近的车间距离保持有序行进的方式，可以确保交通安全，提高交通通行率。

传统车队间车距控制取决于驾驶员丰富的经验以及熟练的车辆控制技能，以确保车辆间的相对距离以及行驶的车速，而智能车车队通过先进的传感器(机器视觉、磁、雷达)来感知和获取前方车辆的距离以及速度。本文根据该信号建立车队跟随控制器，确保车辆与车辆之间的安全距离，使其构成一个不可分割的整体，如图6所示。

假设车身长度均为L，Sdk为第k-1辆车与第k辆车之间的允许安全车距，Sdk+1为第k辆车与第k+1辆车之间的允许安全车距。ua和α为领航车车速和加速度，uak和αk为第k辆车的车速与加速度，uak+1和αk+1为第k+1辆车的车速和加速度。

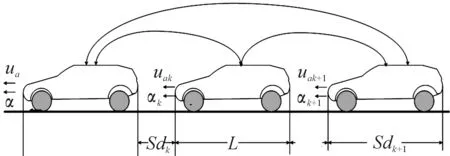
图6 车辆队列行驶简易模型图

2.1 车间间距的控制策略

合理控制车车间距是车队按一定通行率安全行驶的保障。目前，车距算法可分为固定间距算法和可变间距算法，后者又可分为固定车头时距算法和可变车头时距算法[14-15]。本文从安全角度出发采用可变车头时距法，考虑以下几种影响因素：① 所确定的车车间距必须考虑车队当前车速、最大制动减速度等因素；② 兼顾车辆队列行驶的稳定性和交通的通畅性，密度合理，不会造成交通拥堵。

领航车按照给定的ECE城市工况为目标车速行驶，跟随车辆则根据前车的车速以及车辆间的相对距离来控制本车的车速，使得前后车辆车速相近，为了保持车辆队列行驶时的稳定性，要求车车间距的波动率在远离时不超过30%。由于汽车的纵向动力学模型存在很多的不确定性以及非线性因素，本文基于强鲁棒性的智能模糊控制方法，建立车队中各个车辆的跟随控制算法，以实现车辆队列行驶中车车间距的保持，详见2.2节。

另外，车车间距控制策略中被控对象车距的确定对车队稳定性有重要影响，考虑到智能车队车车之间有通讯，因此车车之间的安全距离与当前车速和加/减速度有关系，上述三者之间关系如式(6)所示。车速越大，安全距离越大；加速度越大，安全距离越大；减速度越大，安全距离越小。

Sdk=f(uak，αk)=tuak+ξdbk

(6)

考虑到道路模型的复杂性，队列中第k辆车与前车的实际距离可定义为：

di=Sdk+L

(7)

2.2 基于模糊智能控制的智能汽车跟随模型

针对非线性控制系统，模糊控制策略有良好的鲁棒性，因此根据上述智能汽车车队的车车间距以及车速控制策略，建立智能车队跟随模型。把车速差(Δu)以及距离差(Δd)作为跟随控制器的输入，油门踏板开度以及制动踏板开度作为该控制器的输出。

1) 模糊智能控制器输入输出量以及隶属度函数的选择

根据输入量的特性，其隶属函数选择的是控制效率高、变化快的三角形隶属函数。经过多次调试模型，最终确定了车速差Δu(前一辆车的车速与后一辆车的车速的差值)最佳的论域范围[-1 1]，其模糊子集分为7级，分别为：正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NM)、负大(NP)。同理，经过调试，距离差Δd(前一辆车的车头到后一辆车车头的距离)的论域为[0 1]，模糊子集分为4级，分别是：危险(N)、小(S)、中(M)、大(B)。该控制器的输出分别为油门踏板开度和制动踏板开度，论域为[-1 1]，它们的模糊子集分为7级，分别是：正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NM)、负大(NP)。当输出值范围为(0.1，1]，表明油门踏板信号输出，当输出值范围为[-1，-0.1)，则表明制动踏板信号接入。考虑到减小油门和制动之间的切换次数，当输出值为[-0.1，0.1]时，则表明踏板维持原来的状态。考虑到输入输出量的特点，在模糊子集范围内，无明显峰值，因此选择正态分布型隶属函数。

2) 模糊智能控制器控制规则

根据本文2.1节对跟车控制策略的描述，采用Mamdani’S(min-max)决策法，建立跟随模型的控制规则，如表2所示。

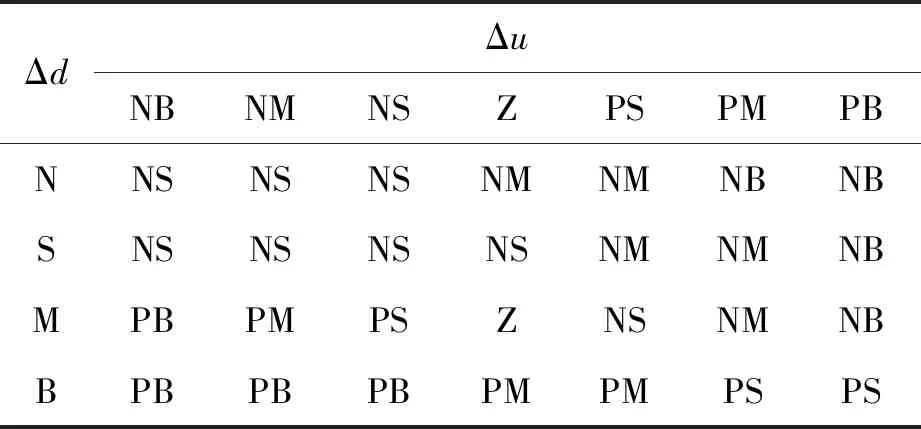
表2 规则变化

3 基于Matlab/Simulink/Stateflow建模以及仿真分析

3.1 智能车队跟随模型

基于上述对领航车的模型和跟车模型的分析，基于Matlab/Simulink仿真平台下，搭建了有3辆车所组成的队列行驶模型，如图7所示。

本研究是由3辆同一款式的汽车构成的车队，其中领航车的驾驶员模型是根据自身的车速与目标车速的差值，以及差值的变化率，通过智能模糊控制方法(详见第1节的结论)来判断领航车的加速程度或者制动大小。1号跟随车的驾驶员模型则需根据和领航车的速度差值以及和领航车的位移差值来判断1号跟随车的油门和制动踏板开度，1号跟随车跟车模型如图8所示。同理，2号跟随车则是根据和1号跟随车的相对速度以及相对距离来控制2号跟随车的油门以及制动踏板的开度。

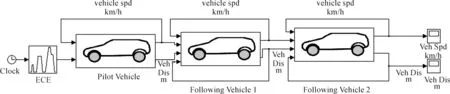
图7 智能车队跟随模型

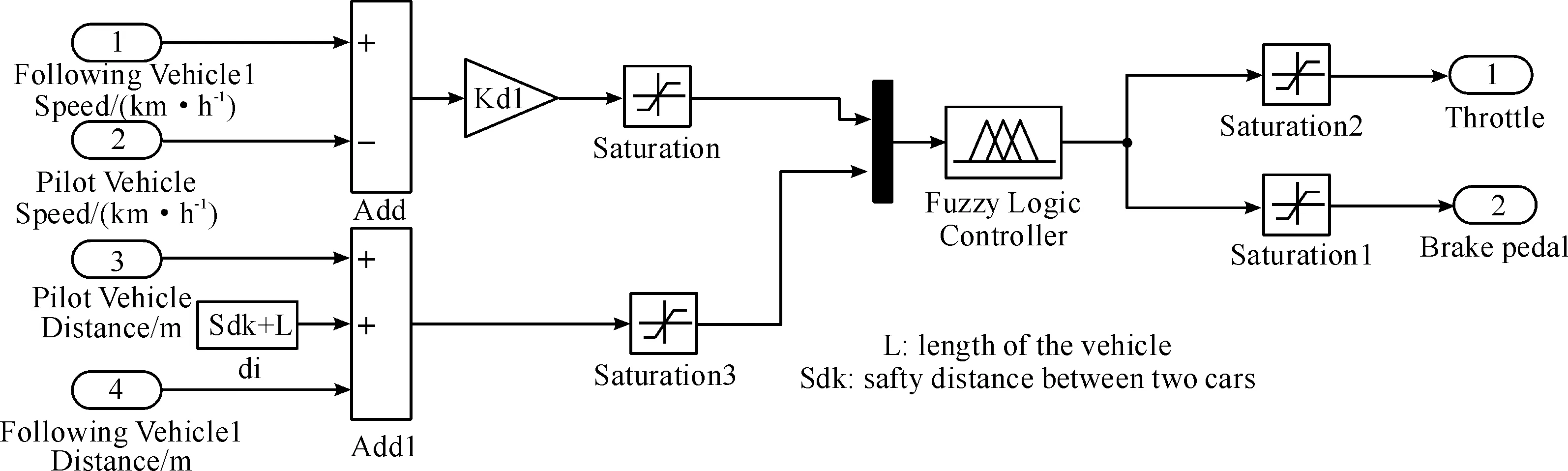
图8 跟随车驾驶员模型

3.2 仿真结果分析

在Matlab/Simulink搭建好模型后，车队各个车辆之间车头与车头之间的初始间距为15 m，根据式(6)可知，车队之间的安全距离随着车速的增加而增加。领航车以ECE城市道路巡航工况的目标车速起步，ECE循环工况仿真时长为196 s。

车队中各个车辆行驶速度随时间的变化如图9所示，图中实线为领航车车速变化趋势，点线为1号跟随车车速变化情况，虚线为2号跟随车车速变化情况。

分析图9可知，车辆行驶速度变化曲线相似，2号跟随车在某些时间节点出现了速度差异，分别是30、90、161.32和181.96 s，将该时间节点的车速进行对比，如表3所示。

图9 队列行驶车辆的速度变化

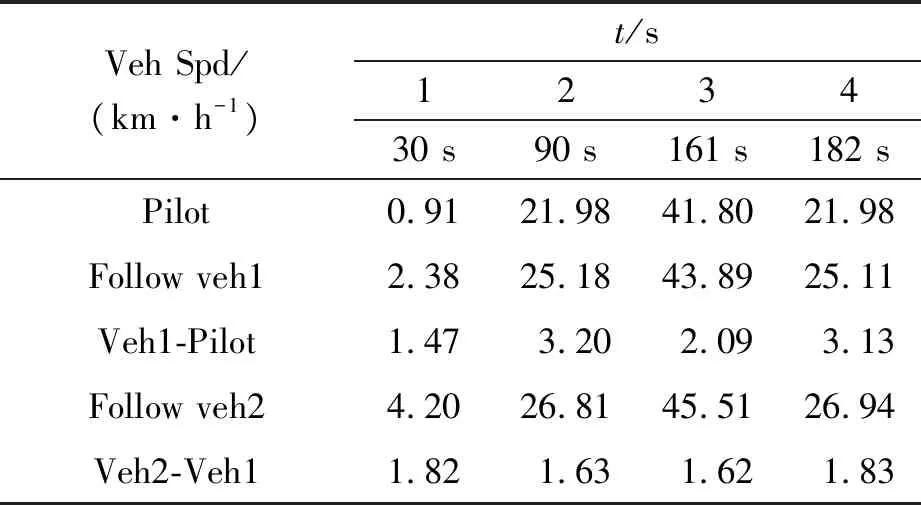
表3 车队行驶特殊节点速度对比

通过表3的数据分析可知，在ECE城市道路循环工况下，最大车速差为3.2 km/h，小于车队行驶车速差的要求，符合车辆队列行驶的跟车车速目标范围。

智能车队在t=0时刻，各个车车头间距以15 m为安全距离，在经过ECE城市道路循环工况后，每辆车行驶距离随时间的变化如图10所示，图中实线、点线和虚线分别为领航车、1号跟随车、2号跟随车的行驶距离变化曲线，可知在ECE城市道路工况下，车队中的各个车辆间距保持较为一致，满足了车队通行效率的要求，其中在98.2、100、118、144.7 、190.2和191 s时间节点车车间距值较大。

图10 队列行驶车辆的距离变化

记录3辆车在上述6个节点所对应的行驶距离，详细变化如表4所示。

表4 队列行驶车辆的距离(d)变化

表4中，ΔDis1代表领航车与1号跟随车之间的距离差，ΔDis2代表1、2号跟随车之间的距离差值。在ECE道路循环过程中，在98、100、190 s时刻，车队两两车头间距均有所减小，最近的情况保持在12 m。在118 s和114.7 s时刻，车车间距有所增加，最大车距保持在19.5 m。为了更好地描述车队间距保持情况，计算了车车间距波动率，如表5所示。

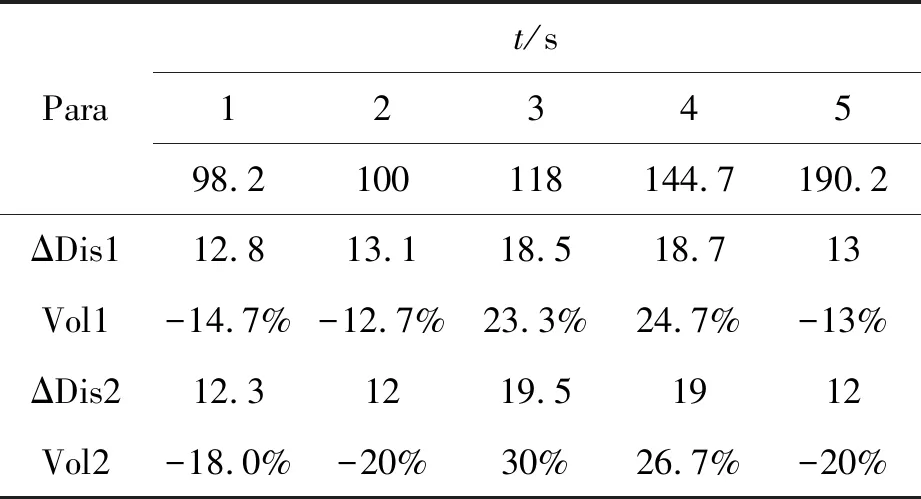
表5 队列行驶车辆的距离(d)波动率

表5中，Vol1代表的是领航车与1号跟随车间距的波动情况，Vol2代表的是1、2号跟随车间距的波动情况，负值代表车车间距在靠近程度，正值代表车车间距在增加程度。

由表5可知，在ECE循环工况下，车车间距在靠近时的最大波动率为20%，在远离时的最大波动率为30%，均小于或等于目标值，满足车队行驶时车车间距的要求。

4 结论

为了提高车队行驶过程的安全和通行率，本文建立了车队车辆跟随模糊控制器、领航车驾驶模糊控制模型以及换挡模型模糊控制模型，并完成车队纵向动力学建模，在给定的ECE城市道路循环工况下，基于Matlab/Simulink/Stateflow仿真平台，对其进行了仿真分析，结果可知，车队中的车辆行驶速度与领航车车速误差值为3.2 km/h，行驶中各车间的距离保持在安全距离，在12～19.5 m。从仿真结果来看，2号跟随车车速与1号跟随车存在差值的原因有以下几点：① 道路模型、车辆各系统模型的建立是采用的理想化的模型；② 模糊逻辑控制策略依赖大量的经验数据进行决策判断，因此会导致结果误差；③ 系统响应滞后，造成跟车反应迟滞；④ 未控制油门变化率，未考虑车辆队列行驶时的能耗优化。

基于以上分析，后续研究工作开展方向为：① 本次设计中未考虑复杂的实际环境以及非线性的动态特性，未来可以考虑。② 未来可以考虑深度学习等控制方法。③ 下一步针对混合动力汽车车队能耗、通过率以及安全性综合研究。