从相对论看在教学中引入物理学史的作用

(天津南开区职工大学，天津 300102)

爱因斯坦的相对论应当是普通物理教学中的内容之一。这也许在普通物理学中并非最重要的内容，但会有学生对此很感兴趣。而且，狭义相对论从数学上来讲并不复杂。而在介绍广义相对论时也不必展示其复杂的数学过程。从物理知识体系的完整性而言，没有狭义相对论，作为电磁学基础的麦克斯韦方程组就不能成立。因此，这部分知识不应被回避。

一、狭义相对论的建立是物理学发展过程中必须的选择

相对论的难点在于观念。牛顿认为：空间和时间是独立于物质世界的运动的特殊存在，与物质世界的任何运动和变化毫无关系。空间和时间也是分别独立存在，彼此毫无关系。总之，时空就是一个容器，与运动无关。并且，时间与空间是分离的。其实，牛顿的时空观也是很抽象的，但他和人们的日常经验相吻合，因此易于被人们所接受。况且，这一时空观在低速宏观条件下也是严格合乎事实的。但是，我们需要从历史的眼光来看一看，为什么人们要修正牛顿时空观，这不仅有悖于人们的“常识”，并且这一时空观在相当广的范围内还是正确的，显然这里面有不得已的理由。

在19世纪末，英国物理学家汤姆逊(Thomson，Joseph John;1856年-1940年)认为物理学作为一个知识体系已经基本完成。当然他也承认Michelson-Morley 实验和黑体辐射所带来的问题。而上述两个问题的解决导致了相对论和量子力学的创立。

现在的人们并不关心“以太”是否存在，当然我们后面还要谈到迈克尔逊——莫雷实验。我们要从历史的角度看待狭义相对论的诞生，还原人们思想的发展脉络，这与学生理解相对论的心路历程应当是一致的。大家都知道，如果说相对论更多的还是满足人们的精神需求的话，那么电磁学就与人们的日常生活及工业生产息息相关了。但电磁学的基础是麦克斯韦方程组。

(1)

但是，一切物理过程都要在一定的时间和地点发生，如果按照以牛顿时空观为基础的伽利略变换

(2)

(3)

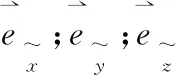
(4)

(5)

而通过(4)所展示的关系来看，如果依据伽利略变换，很难在两个惯性参照系之间形成电磁场麦克斯韦方程组的协变关系。大家知道，电磁学对于我们的生产生活都是至关重要的，我们不可一日无电。但电磁学大厦如果地基不稳固，其后果将是难以预料的。这就把人们逼到了尽头，狭义相对论的出现是一件必须要发生的事情了。

这里不想去详述迈克尔逊莫雷实验的具体内容以及麦克斯韦方程组对于洛伦兹变换的协变性。任何一本电动力学教科书对此的叙述都不厌其烦且千篇一律。人们观察不到在不同的参考系中光速的不同，于是就认定有一种特殊的介质——以太充斥于空间中，而光速是相对于以太而言的，这样既可以解释为什么麦克斯韦方程组中以光速c为常数，又可以找到那个若隐若现的“绝对参考系”，从而做实牛顿的“绝对时空”理论。但迈克尔逊——莫雷实验否定了有这种特殊作用的以太，类似的实验一直做到上世纪80年代(见郭硕鸿《电动力学》)。但一切事实都说明光速不依赖于任何参考系。

进一步理解，对于众所周知的洛伦兹变换

(6)

这一变换使得麦克斯韦方程组在不同参照系下是协变的。与之相对应的不变距离公式就是

ds2=-c2dt2+dx2+dy2+dz2=-c2dt+dl2

(7)

在这里把时间与空间平权了。推广勾股定理，任意两点距离的平方等于其在直角坐标系中各坐标参数的平方的和。这里将时间列为这一“直角”坐标的一维，因时间是无形的，故将相关项前加上虚数符号i，而i2=-1，所以广义的“距离”，即间隔，变成了这个样子。

此时如果引入固有时dτ，固有时是与某运动体系同步的“静止”坐标系测出来的时间，可以引入广义速度，即

基于ds2=-dxμdxμ

(8)

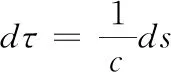
(9)

(10)

(11)

(12)

则4维速度的分量是Uμ=γu(u1,u2,u3,ic)

(13)

上述速度的定义还构成了相对论协变的力学形式，这里不再详述。

二、以历史发展的角度讲解狭义相对论的建立有助于学生的理解

人们为什么要放弃十分熟悉的绝对时空观，转而去建立相对论的时空观？这本身就需要足够的理由。将物理学史引入相对论教学，就向学生揭示了这一理由。为什么讲狭义相对论总是要和迈克尔逊——莫雷实验绑定？这是因为迈克尔逊——莫雷实验否定了“以太”的存在。而在绝对时空观之下，以太是作为“绝对参照系”存在的，所谓的光速就是光线针对这种“绝对参照系”的速度，这就给麦克斯韦方程组中光速为常数的原因以一个勉强的解释，给绝对时空观圆了场。但可惜的是：事实上“以太”是不存在的。

在相对论教学中，教材里都自觉或不自觉地引入了相关的物理学发展史。课程的设计者和讲解者看来都感到面对艰难的相对论(可惜不是难在数学上)，不引入物理学史是不行了。我们可以从大量的普通物理教材中得到映证，这里就不一一详述了。但是，各种教材在引入物理学史方面的力度是不够的。问题在于，面对着“浓缩”的物理教材，学生的理解产生了困难。近年来出现的一些普通物理教材，如潘传芳编著的《人文物理》(2010年8月由科学出版社出版)在这些方面有较大的改观。

三、广义相对论

某些普通物理教材，如赵凯华、罗蔚茵的《新概念物理教程——力学》(高教社1995年出版)已经引入了广义相对论的内容。这是由于广义相对论是公众极为感兴趣的物理学理论，作为物理教材的撰写者不能不考虑到如何增加物理这门课程的吸引力。况且，广义相对论也没有那么神秘，其艰深的数学部分并不需要都讲出来。因此，广义相对论出现在普通物理教材和科普书籍中就不可避免了。

从历史的角度看，怎么出现的广义相对论？这里我们要谈到牛顿的万有引力定律，其表达式为

(14)

我们也可以将万有引力定律方程变成引力势的形式：

(15)

但无论如何在万有引力定律中找不到时间变量，在这一点上万有引力定律不同于电磁场，它仍然奉行“超距”作用。并且(14)式也无法满足洛伦兹变换。现在一切都颠倒过来了，经典时空观能解释万有引力定律，不能解释麦克斯韦方程组。而狭义相对论时空观能解释麦克斯韦方程组，又不能解释万有引力定律了。鉴于物理规律的统一性。总不能在力学部分建立一个时空观，在电磁学部分又建立一个时空观。所以我们要讲到历史，使学生理解理论的发展有其内在逻辑。降低学生理解问题的难度。

爱因斯坦得出的结论是，引力来源于空间的弯曲，这是由于空间的构造造成的，不是因为物体受了任何的力。地球围绕着太阳转，从牛顿引力观来看，是由于两者之间的引力，从广义相对论的观点来看，是由于太阳周围的空间弯曲了，地球是在这一弯曲的时空中做“直线”运动，这是由于地球没有受到任何其它力的影响所产生的必然结果。

我们平时如果在光滑的地板上推出一个小球，小球就会做直线运动，当然最后由于摩擦力的作用它会慢慢停下来。但没有人去思考小球为什么是做直线运动，除非有人以外力去干扰它。广义相对论的回答就是，小球是在平直的空间里沿着空间的构造作直线运动。而在弯曲的时空里，相应的曲线——测地线——就是那里的“直线”。这种思维方式就是将引力几何化，这是很高明的。但一旦这种思维方式被泛化，就不一定合理了。

那么，是什么因素造成了时空的明显弯曲呢？是太阳这样的物体，因为具有天文数量级的质量，造成了时空的明显弯曲。反映这种弯曲的参量是能量—动量四维张量

Tαβ=ρuαuβ

(19)

Tμν=gμαgνβTαβ

(20)

爱因斯坦在1915年提出的引力场方程为

(21)

处于场源物质以外的时空区域，由于只有引力场存在，被称之为“真空”(现代物理学研究证明，其实根本就没有什么真正意义上的真空，这里指的是没有可观测到的物质存在的区域)，在真空中由于Tμν=0,T=0，因此有场方程

Rμν=0

(22)

场为真空，并且引力场状态为静态。在这种边条件极度简化的前提下，Schwarzschild得出了爱因斯坦方程的第一个解：就是Rμν=0的解，其形式为

(23)

(24)

引力场的存在会带来时空状态的一系列变化，所引起的时钟变化为

(25)

在无引力场区域时空的时间用dt表示，引力场区域的时间用dτ表示。根据(25)式，引力的强度与时间的流逝速度成反比。这对于我们所处的环境中来看，当然是匪夷所思。但在弱场条件被破坏的中子星和黑洞的近处这就是现实。

引力场中径向相邻两点间的线元为

(26)

在引力场中，以dr表示引力方向两点的距离。以dl表示引力作用导致此两点距离改变后的距离。根据(26)，引力越大，这两点间的距离就越长。这是时空弯曲的结果。这在我们可以生存的常态星球附近当然是难以见到的情况。其实，正是在广义相对论提出后陆续发现的中子星、黑洞等等天文现象使得人们不得不承认和使用广义相对论，因为万有引力定律此时已经无能为力了。

根据Schwarzschild解的数学表达式，只有当

(27)

一般星体的实际半径都远远大于其引力半径。太阳的引力半径不足三公里，地球的引力半径不足一厘米。如果物体的体积全部收缩到引力半径之内，这个物体外部时间就看不到它了，连光线都跑不出来，就形成了被人们称之为黑洞的星体，尽管如此，在2019年北京时间4月10日晚上9点7分，人类首次拍摄到的黑洞照片在全球六地还是同时发布了。

对于黑洞的探索目前所带来的文化效应远大于其在科学技术的上的意义。当前解决黑洞问题的主要依据是爱因斯坦引力场方程，以及对此方程的两个精确解，即Schwarzschild解(1916年)和K. P. Kerr解(1963年)，后者是真空中场方程动态的轴对称解。这两个解其数学推演当然是很繁杂的，但其解并不复杂。这些解说明时空的结构确实是很复杂的。

首先我们应当注意到Schwarzschild解

g00=0,g00=,g11=,g11=0，为了尽量减少直至消除时空奇点，物理学家尽量选取合理的坐标系。到了1960年，M·D·Kruskal和G·Szekeres建立了Kruskal坐标系，这个坐标系是根据实际需要设计出来，由实际效果来检验的，它不需要数学证明。关于Kruskal度规给广义相对论理论带来的进展，作者在《天津职业院校联合学报》2013年第11期发表的《浅谈广义相对论》中有详细阐述，在此不拟重复。

实际上任何一个物理模型再加上其数学表达式，都不可能反映出客体的全部规律。因为任何物理模型，都必须对研究对象进行简化，都不可能反映出被研究对象的全部物理性质。如果面面俱到，不去抓主要矛盾，就不可能建立起任何物理模型。但一旦情况发生了变化，原先被忽略的物理要素就会变得无法忽视，因而原先确立的物理模型就不再真实，就无法作为被研究对象。这时物理模型就应当修改。我们实际上并没有找到“黑洞”运作的规律，使用Kruskal度规，也无法消除Scharzchild解的内禀奇点，此处就是物理规律失效的地方。这与目前相对论与量子力学的不相容有关。就是说如果能证明在物理学范畴内R不可能无止境地趋于零，因为自然界也是量子化的，这一奇点的问题就可以解决。

四、在相对论教学中引入相对论发展史的意义

上述依照物理学史发展的脉络对狭义相对论和广义相对论进行叙述，挂一漏万，比较粗糙。但由此也可以看出，物理学史实际上也是物理学的一部分，不宜人为分开。否则让人如何理解为何会出现相对论，人们为什么要抛弃与人们日常经验相符，并且在相当大的科学技术范围内仍然是相当正确的牛顿时空观？大家可以看到，相对论，尤其是狭义相对论，其数学手段相当简单，但人们容易理解吗？但相对论已经深深地融入了现代文化当中，成为公众感兴趣的话题。而不是局限于物理学之内，不是只有少数人才需要知道的知识。物理教师无论如何也是物理学的“业内人士”，有责任和义务普及这一知识。而将相对论与相对论发展史融为一体是讲解相对论这一理论的最好方法。