空间非合作目标自旋速率测量方法与实验

王 立，顾营迎，郭绍刚，李 涛，储 怡

(1.北京控制工程研究所 光电事业部，北京100190;2.佳木斯大学 理学院基础物理部，黑龙江 佳木斯 154002)

引言

实现对空间非合作目标运动状态的测量是当前的热点研究领域[1-2]。常用的测量方案有主动激光雷达、被动双目相机、被动单目相机和结构光相机等[3-4]。在实际的应用中，由于对非合作目标运动状态的测量有一个由远及近、由粗略估计到精确测量、由目标快速自旋到消旋降速的过程，同时整个过程中的光照环境条件各异，所以很难有一种测量方案可以应对全过程的测量需求，大多的研究方案都有其应用的针对性和适应性[5-8]。

单目相机具有体积小、功耗低、成像信息丰富、配置应用方便等特点，利用单目相机实现部分非合作目标运动状态的测量、估计，可以很好地实现与其他测量手段的数据融合，增加系统测量数据的可靠性。Nassir实现一种基于单目相机的近距离、有光照反射条件下的非合作目标位姿测量方法，该方法运用了矢量量化和单词树检索技术[9]；Sharma 系统比较了3种基于单目相机的空间目标位姿估计方法，考虑了空间环境应用的特殊性，如计算资源有限、图像信噪比低和对比度高等，并给出了算法比较结果和改进建议[10]；Particular 提出一种非合作目标相对位置、速度、姿态和形状的滤波估计方法，利用了单目相机和距离敏感器的原始数据[11]；Tzschichholz 提出一种利用3D-TOF相机和高分辨率单目相机相结合的非合作目标相对位姿测量方法，可以实现60 Hz的测量实时性[12]；Mingfeng提出一种准最优化的单目图像特征点提取方法，运用该方法可以实现单目图像特征点的散布选取，从而提高基于特征点的相对位姿测量的精度[13]。

本文主要研究利用单目相机图像，在中、远距离段，实现高速自旋的非合作目标自旋速率的测量。该方法主要有如下几个特点：作用距离远，目标在图像上具有可见的几何形态特征即可实现测量；测量精度高，本方法提取的自旋周期性特征稳定、可靠，不易受到光照环境变化的影响；对单目相机的成像帧频要求不高，可以实现基于低帧频图像的高速自旋目标的测量。

1 测量原理及方法

1.1 测量系统坐标系定义

空间非合作目标相对运动状态的测量，涉及到追踪卫星和目标卫星两个实体，为了描述他们之间的关系，需要定义追踪卫星本体坐标系、目标卫星本体坐标系、传感器坐标系、图像坐标系等几个坐标系。

如图1所示，在追踪卫星质心处的坐标系C，定义为追踪卫星本体坐标系；在目标卫星质心处的坐标系{A}，定义为目标卫星本体坐标系；坐标系{S}定义为单目相机坐标系；图2中的坐标系{M}定义为单目相机的图像坐标系。

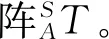
1.2 自旋目标与像面投影的周期性关系

如图1、图2所示，对于目标卫星帆板上的一点p，通过单目相机成像在图像坐标系{M}上，其与坐标系原点oM的连线与坐标轴oMxM成一夹角θ′。当目标卫星发生快速稳定自旋时，由于目标卫星上的点与卫星是刚性固连的，也就相当于射线oAp绕旋转轴旋转，因此射线oAp的自旋速率等效于目标卫星的自旋速率，如果获得了oAp自旋周期与其在单目相机像面上的投影角θ′变化的关系，就可以通过测量投影角θ′的变化来获得目标卫星的自旋速率。

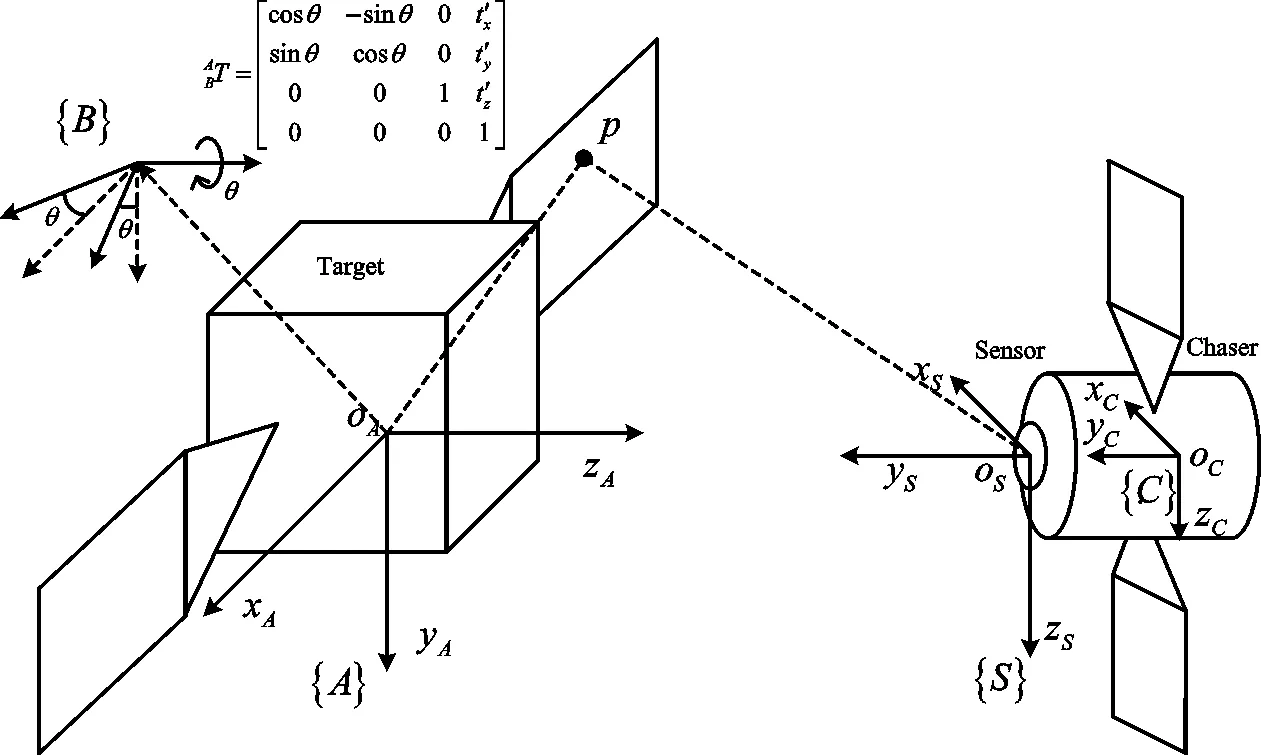
图1 测量系统坐标系Fig.1 Measuring system coordinate system

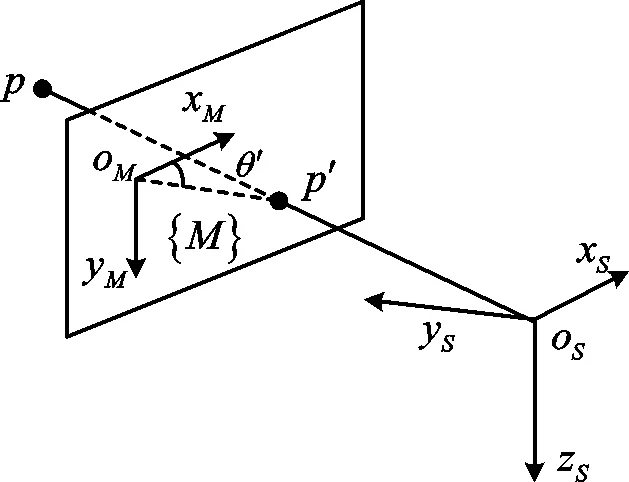
图2 图像坐标系与投影点Fig.2 Image coordinate system and projection

空间非合作目标的姿态，都是相对于追踪卫星的，因此为了描述方便，将世界坐标系{W}设定在单目相机坐标系{S}处。如图2所示，根据小孔成像原理，对于坐标系{A}下的一点p来说，该点在坐标系{M}下可用下式表达：

(1)

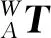
因此有：

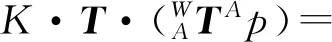
(2)

如图1所示，当目标卫星发生自旋运动后，坐标系{A}变动到了坐标系{B}后，点p在单目相机图像坐标系{M}下的表达为

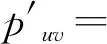
(3)

(4)

所以，根据(3)式有：

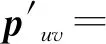
(5)

根据(5)式，可以得到坐标系{M}下投影点p′的坐标{u′,v′}：

(6)

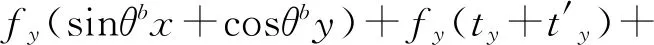
(7)

观察(6)式、(7)式，在远距离观测高速自旋的卫星目标时，短时间内坐标系{A}相对于世界坐标系{W}的平移矩阵和坐标系{B}相对于坐标系{A}的平移矩阵都可以近似为零，因此可以得到目标卫星自旋角度θ与其到单目相机图像坐标系的投影角度θ′之间的关系：

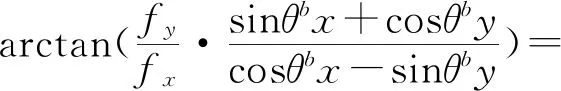
arcan(tan(θ+φ))

(8)

通过上式，可以看到如图3所示，当目标卫星自旋角度θ以2π为周期时，投影到单目相机图像上的角度θ′以π为周期变化，同时二者在相位上相差了φ。因此通过对目标的单目观测成像，可以测量其自旋周期。

图3 sin(θ)与θ′的序列曲线Fig.3 Sequence curve of sin(θ) and θ′

1.3 目标投影稳定区域处理方案

根据上节的分析证明可知，理论上目标卫星上任意点到本体坐标原点连线的投影夹角变化都可以表征目标卫星自旋的信息。但是在卫星自旋的过程中，这种点会被遮挡或者由于光照条件的影响造成点跟踪的失效，从而导致算法失效。

为了实现目标卫星自旋信息的测量，通过实验发现，在目标卫星自旋过程中，由于卫星主体和太阳帆板的包覆材料反射特性的差异，导致中、远距离对目标卫星成像后，目标卫星的外轮廓具有稳定的特征。因此本文选择卫星的稳定外轮廓特征来代替易失效的点特征，并将外轮廓特征线性化，求其与图像坐标系x轴的夹角θ′，进而实现目标卫星自旋信息的测量。

在具体的实现方法上如图4所示，首先获得原始的图像，接着提取图像目标的MSER特征区域，对MSER特征区域进行椭圆拟合，并求得椭圆的长轴，最后求得椭圆长轴与图像坐标系x轴的夹角，以此来实现目标卫星自旋速率的估计。

图4 卫星投影角θ′图像处理步骤Fig.4 Image processing steps of satellite projection angle θ′

1.4 自旋速率估计方法

根据上节的证明可知，自旋目标卫星的自旋周期为其在像面投影夹角变化周期的两倍。因此获得自旋目标卫星自旋速率、自旋周期的方法，就是根据序列θ′值，估计出其变化周期。

估计一组序列值周期的方法有很多，常见的有频谱分析法、最大最小值计数法等等。实际工程应用中获得的θ′值序列会受到各种噪声和其他误差的影响，导致序列每周期的极大值和极小值不尽相同，过零点的偏置值也不相同。

为了解决如上问题，本文应用正弦多项式来拟合序列曲线θ′值。通过单目相机对中、远距离目标卫星成像后，获得的θ′值序列，主要由短周期和长周期两种成份组成。短周期成份是我们要求的θ′变化周期，而长周期成份主要是由于光照角度变化或追踪卫星与目标卫星相对位置关系微小变化等因素所导致的。因此设定周期序列拟合的模型公式为

y=a1sin(b1x+c1)+a2sin(b2x+c2)

(9)

式中：a1、a2分别代表长、短周期的幅值；b1、b2分别代表长、短周期的角速度；c1、c2分别代表长、短周期的相移。

当依照上述模型公式对序列值θ′进行多项式拟合后，可以求出公式(9)中的各项系数。

因此，根据单目相机的成像帧频f，就可以得到目标卫星自旋的速率ω：

ω=b2f/2

(10)

1.5 方法的适用性分析

在测旋方法的适用条件方面，要求在短时间的序列图像观测过程中，相机、非合作目标卫星、太阳三者间构成的空间相角的变化不能过大。主要原因是：一方面因为本方法推导的过程中假设了观测相机与观测目标间的位置关系是固定的，只有姿态关系发生变化；另一方面在空间相角变化的条件下，目标表面对光照的反射特性会发生较大变化，使目标的光照特性不稳定。对于远距离目标的短时观测，尤其是对快旋目标的短时观测，以上空间相角不变的前提约束，在实际的工程应用中是可以满足的。

在测量范围方面，根据(8)式自旋速率估计原理和采样定理可知，只要相机在目标的一个自旋周期内至少采样3次以上，在已知相机帧频的情况下就可以实现目标自旋速率的精确测量。为了获得较高的测旋精度，实际应用中需要缓存10帧以上的观测数据，再进行(9)式所示的周期拟合。

在应用限制方面，主要有对目标的观测方位限制和几何外形限制。由于测旋方法中应用了自旋目标的特征投影角进行计算，因此要求单目相机的光轴不能在目标自旋所形成的平面内，否则算法将无法有效提取目标自旋的特征投影角。另一方面，要求单目相机所观测目标的几何外形不能为球体等无显著长、宽、高比的目标。

2 实验与结果

为了验证本文提出算法的有效性，开展了基于高速自旋卫星在轨真实图像的自旋速率解算试验。

试验中，通过建立与目标卫星的通讯联系，可知目标卫星的实际自旋速率为60°/s。试验中，单目相机的拍摄帧频为1 Hz，如图5所示为从单目序列图像中获取的卫星投影角序列曲线。

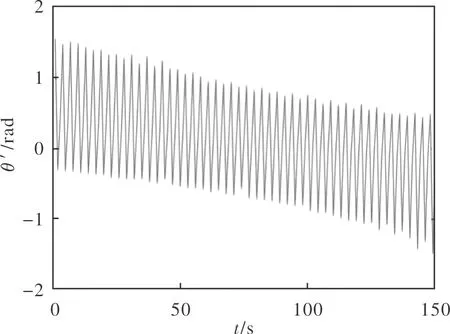
图5 在轨图像实测θ′序列曲线Fig.5 Curve of θ′ from on-orbit images

为了实现卫星自旋速率的连续测量，试验中采用缓存的模式，当卫星投影角θ′的序列值缓存到一定数值n时，开始进行卫星自旋速率的计算。本试验中缓存的数值n设定为19，在150 s的时间内对目标卫星自旋速率连续测量，获得的连续测量结果如图6所示，试验中测量得到的卫星速率的均值为60.07°/s，标准差为0.05°/s。

3 结论

本文提出了一种基于单目相机的快旋空间非合作目标自旋速率测量方法。通过测量原理的数学证明、在轨图像数据的测试，证明了本文提出的目标自旋速率测量方法的可行性和有效性。以在轨图像数据为输入的实验结果表明：对于60°/s的快旋非合作目标，本方法的测量均值为60.07°，标准偏差为0.05°/s。在中、远距离目标图像细节退化严重、自旋速度快的情况下，本文给出的方法为空间目标运动状态的精确测量提供了一种新的思路和工程化方法。