基于最小二乘法和卡尔曼滤波算法的平面电子罗盘误差补偿方法研究

2019-12-13张一帆杨薇薇

宿州学院学报 2019年11期

李蓉，张一帆,杨薇薇

1.淮南职业技术学院信息与电气工程系，安徽淮南,232001；2.安徽理工大学电气与信息工程学院，安徽淮南,232001

相较于传统指针式罗盘和平衡架结构罗盘，电子罗盘(又称数字指南针)具有能耗低、体积小、重量轻、精度高、可微型化等优点，被广泛运用于汽车、航海、无人机导航等领域[1]。电子罗盘在使用时，易受外界硬、软磁干扰产生测量误差，硬磁干扰通常会导致电子罗盘产生零点漂移；软磁干扰则会导致随机误差的产生，硬磁干扰与软磁干扰产生的误差互相独立。

目前对电子罗盘受到的硬、软磁干扰产生的误差进行补偿的方法有很多。李智、秦涛等人提出基于椭圆假设的误差补偿方法[2-4]，可同时对电子罗盘的硬、软磁干扰进行补偿，其特点是精度较高，但计算量过大导致应用场景有限。胡超等人提出的罗差补偿系数法[5]只能对电子罗盘的软磁干扰进行补偿，无法补偿电子罗盘受到的硬磁干扰，应用场景单一。Fang J提出的基于最小二乘法(Least squares,LS)的椭圆拟合的误差补偿方法[6]，对应用场景的要求较为苛刻，不具有广泛性。Bonnet S提出了标定传感器采集数据，利用椭球拟合对误差进行补偿的方法[7]，但该方法忽略了传感器自身噪声的影响，从而导致精度较低。

针对现有电子罗盘误差补偿方法中存在计算量过大、应用场景有限、补偿精度较低等问题，提出了一种基于最小二乘法和卡尔曼滤波算法(LS-KF)的误差补偿方法，分别对电子罗盘的硬、软磁干扰误差进行补偿，并结合Allan方差分析法对实验结果进行定量分析。该方法可有效补偿电子罗盘测量误差，同时具有计算量小，应用场景丰富的特点。

1 电子罗盘LS-KF误差补偿方法

1.1 电子罗盘的LS硬磁干扰误差补偿

电子罗盘在实际使用过程中会受到外部环境的硬磁干扰产生零点漂移，从而导致测量误差的产生。可使用最小二乘法对硬磁干扰导致的误差进行补偿。

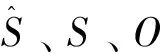
(1)

(2)

式(2)中，Sx，Sy分别表示电子罗盘真实值S的X轴方向和Y轴方向的向量。

(3)

式(3)中，Ox，Oy分别表示电子罗盘零点漂移量O的X轴方向和Y轴方向的数值，三个变量之间的关系可由一个数学模型来表示：

(4)

在理想状态下，电子罗盘实测数据即为真实值，没有测量误差存在,Ox，Oy的值为零。STS为一常数U2，是为本地磁场强度平方

(5)

在实际测量环境中，Ox，Oy的值不为零，因此，实测电子罗盘第i个测量值误差

(6)

可将式(6)简写为：

(7)

式(7)中

(8)

式(8)中,D2为电子罗盘任意一点真实值Sx(i)和Sy(i)平方的和。

假设电子罗盘任意一点测量值的坐标到以电子罗盘零点漂移量Ox、Oy的数值为坐标点的距离都相等。

由式(8)可知实测电子罗盘轨迹形如以电子罗盘零点漂移量Ox、Oy的数值为圆心的，半径为D的标准圆。

将测量所得n组样本带入(6)式中并写成矩阵形式有

r=Y-Fβ

(9)

式(9)中:

(10)

(11)

(12)

根据最小二乘法理论有

rTr=(Y-Fβ)T(Y-Fβ)

(13)

令J=rTr，设存在β，使得J=min对β求偏导，则有

(14)

可得

β=(FTF)-1(FTY)

(15)

将测量数据代入式(10)(11)中，可得矩阵Y、F的值；将Y、F代入式(15)中，可进一步求得矩阵β的值，从而可得电子罗盘零点漂移量Ox、Oy。

1.2 电子罗盘的KF软磁干扰误差补偿

电子罗盘在实际使用过程中，受外部环境的软磁干扰会产生随机噪声，随机噪声是导致测量误差存在的主要原因。电子罗盘受软磁干扰产生的随机噪声属于高斯白噪声。

卡尔曼滤波算法可对带有高斯白噪声的线性系统进行估计[8-10]，该滤波算法是目前应用最为广泛的一种滤波方法，在通信、导航、制导与控制等领域都得到了较好的应用。其基本思想是以最小均方误差准则作为最佳估计准则，通过递推理论实现对系统未来状态量的估计，使得估计值尽可能接近真实值。卡尔曼滤波算法的数学模型如下：

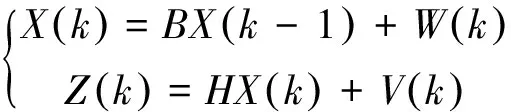
(16)

式中，X(k)为k时刻电子罗盘状态量；Z(k)为k时刻电子罗盘的测量值；假设W(k)、V(k)是互相独立的高斯白噪声；其协方差分别为Q、R，W(k)为输入噪声；V(k)为观测噪声；B为状态转移矩阵。H是系统测量矩阵。

卡尔曼滤波具体递推过程如下：

(1)利用系统k-1时刻的状态预测系统k时刻的状态：

X(k|k-1)=BX(k-1|k-1)

(17)

式(17)中，X(k|k-1)是利用系统k-1时刻的状态预测得到的系统k时刻的状态，X(k-1|k-1)是系统k-1时刻状态的最优结果。

(2)更新系统的协方差矩阵：

P(k|k-1)=BP(k-1|k-1)BT+Q

(18)

式中,P(k|k-1)是X(k|k-1)对应的协方差，P(k-1|k-1)是X(k-1|k-1)对应的协方差。

(3)计算系统k时刻状态的最优估算

X(k|k)=X(k|k-1)+Kg(k)(Z(K)-HX(k|k-1))

(19)

式中，Kg为系统的卡尔曼增益

(20)

(4)更新系统k时刻下系统状态的协方差

P(k|k)=(1-Kg(k)H)P(k|k-1)

(21)

当系统进入k+1状态时，P(k|k)就是式(18)的P(k-1|k-1)。这样，系统就可以通过不断迭代的计算，更新各时刻的系统状态量，从而得到系统状态的最优估计值。

在该研究模型中，将系统的状态转移矩阵B和系统的测量矩阵H设置为1，同样，将系统的卡尔曼增益Kg以及系统的协方差P的初始值也设置为1，即可进行卡尔曼滤波。

2 基于Allan方差的误差分析

Allan方差分析法是由David Allan[11]提出的一种基于时域的误差分析方法，具有便于计算、易于分离等优点，能够定量地对传感器各项不同的误差进行细致的表征和辨识[12-14]。因此本文采用Allan方差分析法对经过LS-KF误差补偿前后的电子罗盘随机误差进行分析，并将其作为LS-KF误差补偿方法的性能评价指标。

2.1 Allan方差基本定义

样本信号长度为N的电子罗盘采集数据，其采样周期为T。将样本分成L组，每组含M(MN-1/2)个样本点,则每组的相关时间τ=M·T，计算每一组的平均值[15]：

(22)

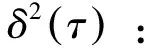
(23)

其中，Allan方差的平方根即为Allan标准差。

2.2 电子罗盘随机噪声的Allan方差

电子罗盘在受到外部磁场干扰的情况下，所产生的随机噪声主要有量化噪声QN、零偏不稳定性噪声BI;可用Allan方差分析法对这两项噪声进行辨识分析[16-18]，各噪声源互相独立。量化噪声的Allan方差为:

(24)

零偏不稳定性噪声的Allan方差为:

(25)

鉴于电子罗盘的量化噪声和零偏不稳定性噪声互相独立，所以电子罗盘噪声的Allan方差分析结果如式(26)所示

(26)

(27)

(28)

由式可以求得各Allan方差的估计值

3 实验数据及结果分析

3.1 数据采集

实验使用HMC5883L电子罗盘采集数据，采样时间为0.1 s，通过Arduino UNO的I2C通信总线读取测量数据。通过串口转接模块将所得数据发送至笔记本，笔记本使用MATLAB接收数据并保存。数据采集环境如图1所示。

图1 电子罗盘数据采集环境

3.2 实验结果分析

3.2.1 硬磁干扰误差补偿结果分析

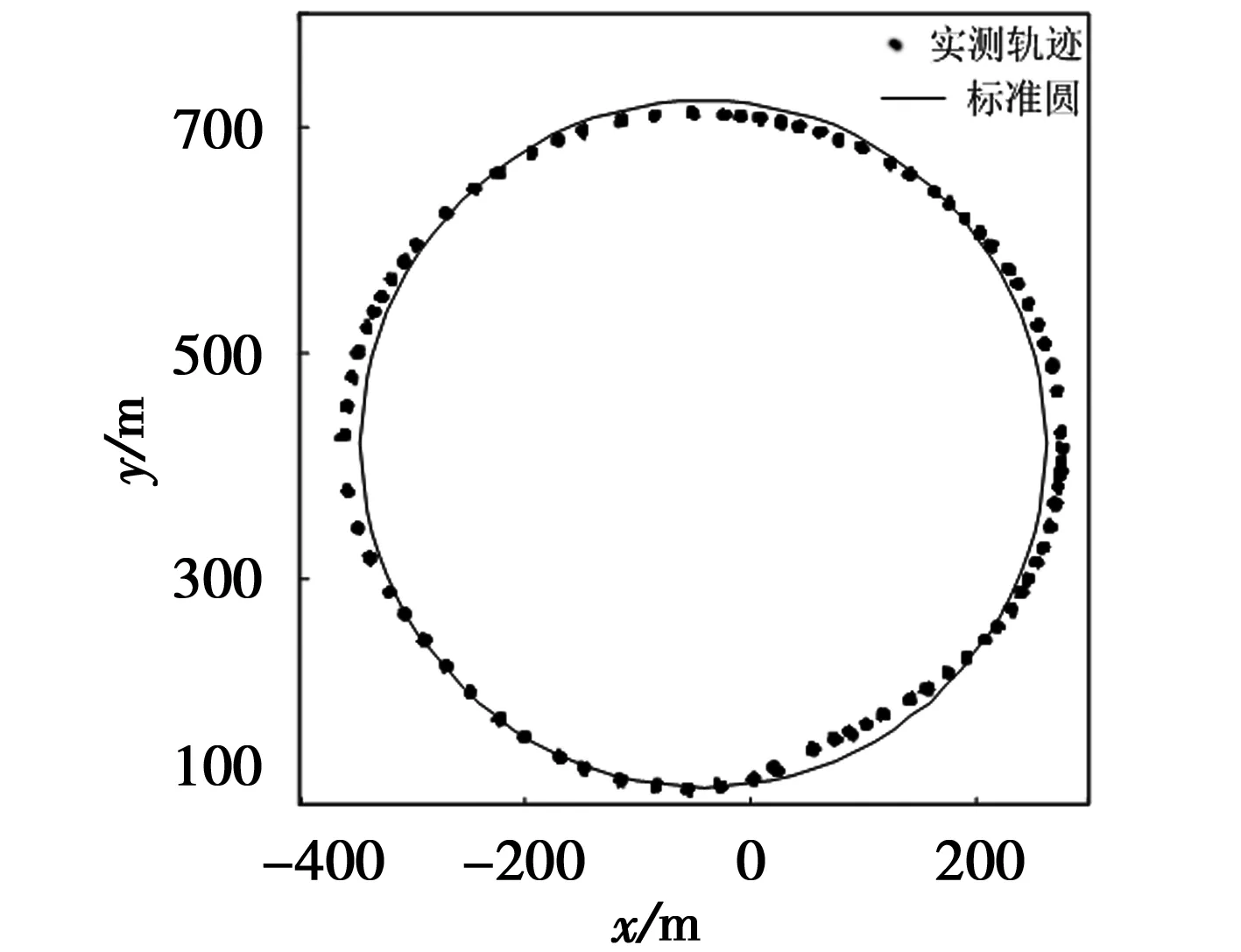
图2 实测数据轨迹与标准圆对比

假设实测电子罗盘轨迹为标准圆是基于最小二乘法对电子罗盘硬磁干扰误差进行补偿的前提，因此需要将实测电子罗盘轨迹与标准圆对比。

实测电子罗盘数据轨迹与标准圆的对比如图2所示，测算后可得，实测电子罗盘数据轨迹与标准圆最大相对误差为4%，在误差允许的范围内；因此，可使用最小二乘法对电子罗盘硬磁干扰误差进行补偿。

由图3、图4可知，补偿后的电子罗盘数据轨迹的圆心从(-42.092 8,419.273)处转移到了(0,0)处。结果显示，最小二乘法可对电子罗盘硬磁干扰误差进行有效补偿。

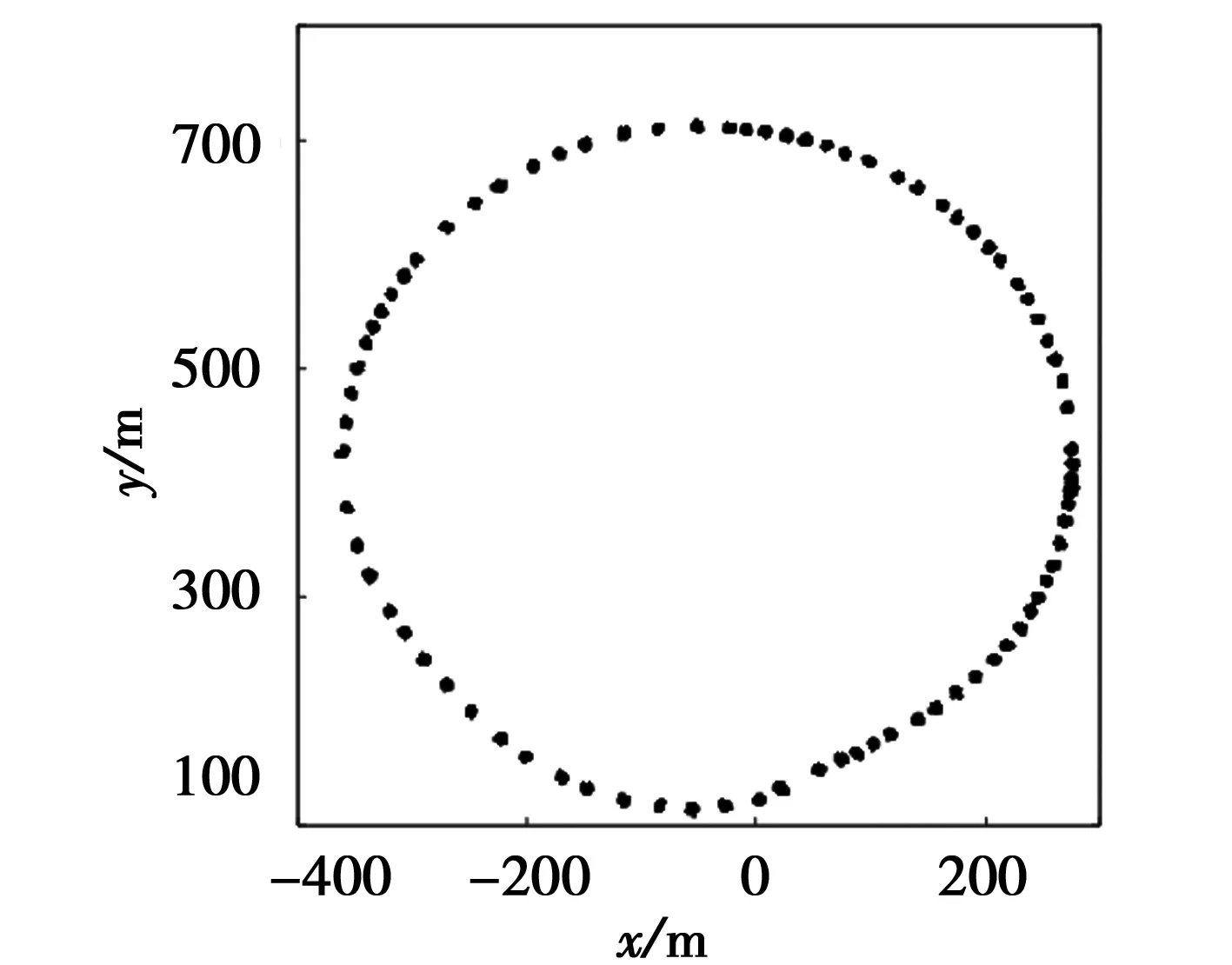
图3 对硬磁干扰补偿前电子罗盘数据轨迹

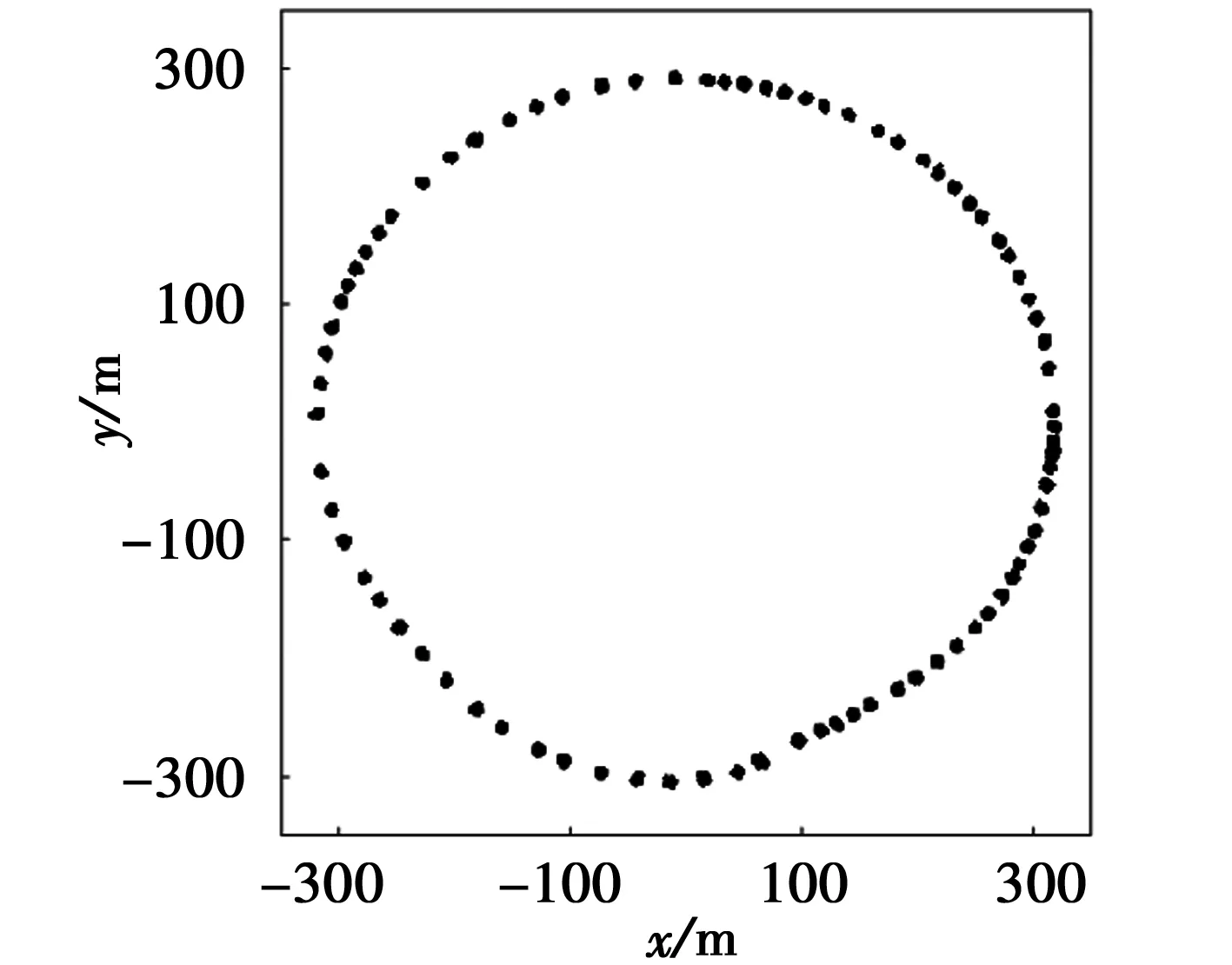
图4 对硬磁干扰补偿后电子罗盘轨迹

3.2.2 软磁干扰补偿结果分析

在对电子罗盘进行硬磁干扰补偿后，进一步利用卡尔曼滤波对电子罗盘实测数据进行软磁干扰误差补偿。

电子罗盘x轴原始数据如图5所示，对原始数据进行测算，其均值为0.002 2，方差为1.371 7。

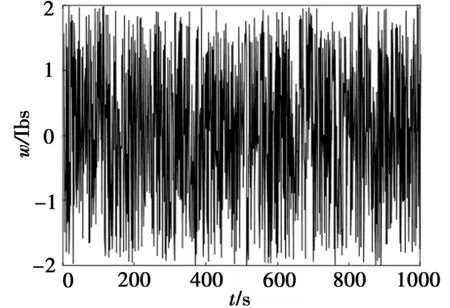
图5 卡尔曼滤波前电子罗盘X轴数据

对电子罗盘x轴原始数据进行卡尔曼滤波误差补偿，结果如图6所示。对补偿后的数据进行测算，其均值为-0.007 5，方差为0.012 9。相较于原始数据，经由卡尔曼滤波补偿后，电子罗盘x轴数据的均值和方差均有明显下降。

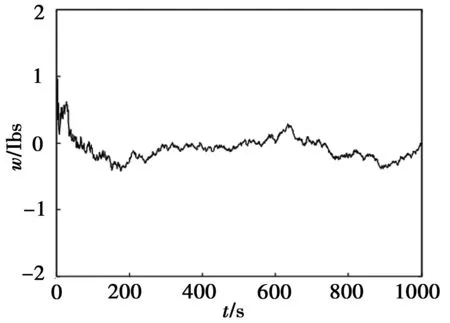
图6 卡尔曼滤波后电子罗盘x轴数据

使用Allan方差分析法对实验结果进行分析计算，并绘制Allan方差曲线，Allan方差曲线对比如图7所示。

由图7可以看出，经由卡尔曼滤波补偿后，电子罗盘x轴数据随机误差的Allan方差值有明显的下降；与图5、图6的表现相符。

图7 卡尔曼滤波前后Allan方差对比

使用最小二乘法对实验所得的Allan方差曲线进行拟合，可得到各误差项的值。滤波后的量化噪声和零偏不稳定性噪声的Allan方差值分别由0.000 935和0.160 291，降到了0.000 161和0.035 448。经过补偿后量化噪声和零偏不稳定性噪声分别减小了82.8%和77.9%，实验结果表明，基于LS-KF的误差补偿方法能对电子罗盘受硬、软磁干扰产生的误差进行有效补偿。