折流圈结构对折流杆换热器壳程的性能仿真与优化研究
2019-12-13张秀香胡崇举牛晓飞
张秀香,胡崇举,牛晓飞,李 强
宿州学院 1.机械与电子工程学院;2.化学化工学院,安徽宿州,234000
折流杆换热器相对于传统折流板换热器具有抗振能力好,传热综合性能优良等特点[1,2],广泛应用在化工、炼油、制药和其他新能源行业。折流杆换热器采用折流栅代替折流板,使得流体主流流动由横向流变成沿着换热管方向的纵向流动,从而有效地降低了流体诱导振动[3-6]。自20世纪70年代美国菲利普石油公司成功开发出折流杆换热器以来,国内许多学者对折流杆换热器进行了大量的研究。在理论方面,董其伍通过实验的方法分别提出了壳程流动与传热的准数关系式[7];在强化传热研究方面,严文良对三角形布管方式的波形折流杆进行了工业实验研究,探讨了其传热性能和壳程流体阻力特性,并提出了对流传热准数关系式[8]。王双英等采用数值模拟的方法,研究了不同折流杆类型的折流杆换热器流动与传热的影响,得出了在综合性能上圆杆要优于方杆的结果[9]。王新婷等提出一种新型波形折流杆换热器,该换热器结构紧凑,当采用水为介质时,与直杆换热器对比,综合性能提升近10%[10]。以上学者对折流杆换热器的强化传热的研究主要集中在对折流杆和开发高效换热管的研究上,而作为扰流的另一重要结构折流圈的研究较少。本文采用CFD软件Fluent通过“分段建模、分段分网、分段模拟、最后综合”[11-13]的数值模拟研究思路对不同壳体直径,不同折流圈宽度与壳体内径比的折流杆换热器进行了仿真研究,得出了最佳折流圈宽度与壳体内径比,为折流圈的设计提供了一定的指导作用。
1 折流杆换热器模型建立
本次折流杆换热器采用全模型的方式,由于本次研究只限于壳程,管程流体忽略,直接在管内壁加载固壁温度,管箱忽略。折流杆换热器按照流体纵向流动特性,可以分成布管限定圆内部的纵流,折流圈内径到外径的旁流,和折流圈外径到壳体内径的间隙流。由于间隙较小,间隙流对壳体流动与传热影响较小,忽略间隙流。表1所示为几何模型主要结构尺寸。
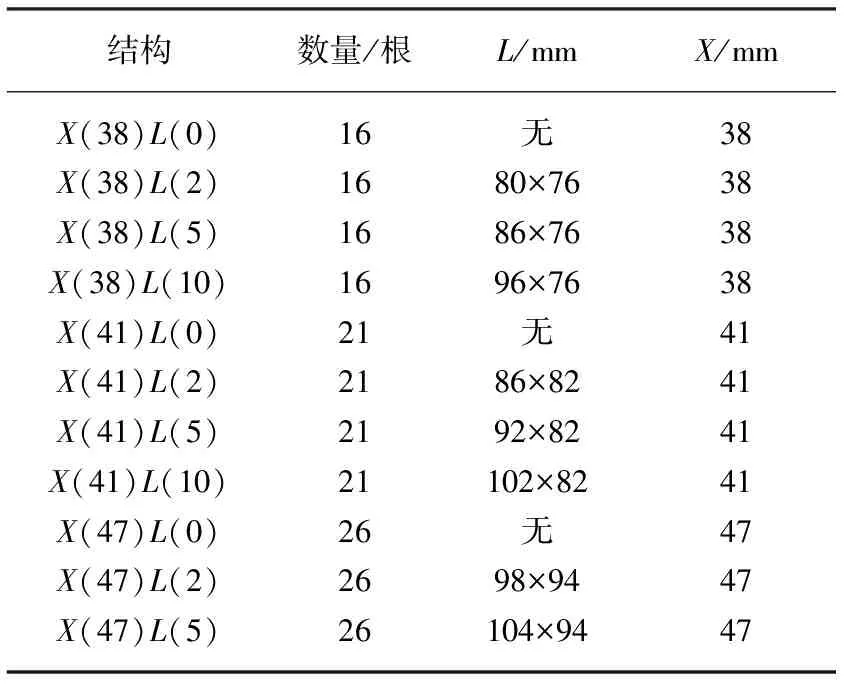
表1 几何模型主要结构尺寸
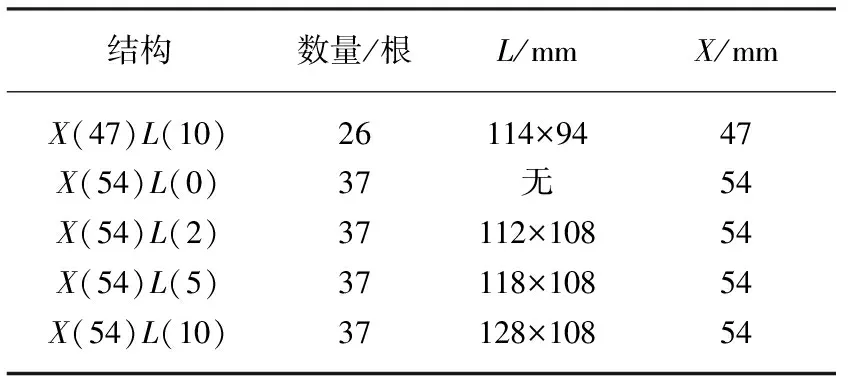
(续表)
其中X表示布管限定圆半径,L表示折流圈宽度。其他参数包括换热管规格∮12 mm×2 mm,折流栅数目24块,折流杆直径∮2 mm,管程为饱和水蒸气,壳程为水。由于折流杆换热器结构较复杂,本文将折流杆换热器分成入口段,六个折流栅段和出口段。以X(41)为例,图1为不同折流圈宽度折流栅处断面图。
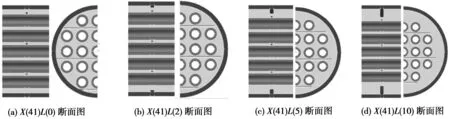
图1 折流栅断面图
2 折流杆换热器计算与仿真
2.1 折流杆换热器计算模型
由于折流杆换热器结构复杂,为了尽量将所有结构保留,采取分段建模和分段划网的方式。图2为折流杆换热器的导流筒段和折流栅段网格划分模型。
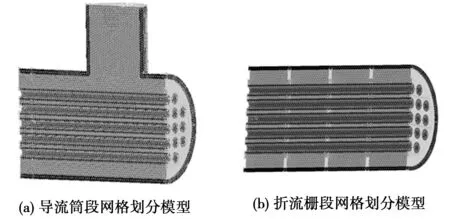
图2 折流杆换热器网格划分模型
为简化计算分别对两段结构做如下假设:(1)由于管程为高温饱和水蒸气,且只关心壳程流动与传热,将内管壁温度设为定值;(2)壳程冷却水为不可压缩连续流体,各向同性;(3)忽略重力影响;(4)流体的物性参数ρ、μ、cp、λ等,为了尽量考虑温度对其的影响,在仿真实验的温度范围内,将其看成为温度的线性函数,简化后导流筒段和折流栅段控制方程为:
(1)
运动方程:
x方向: (u·)p+υ2u
(2)
y方向:(v·)p+υ2v
(3)
z方向: (w·)p+υ2w
(4)
能量方程:
(5)
为了提高湍流计算精度,近壁面与远壁面采取不同湍流控制方程,其中近壁面方程如下:
(6)
(7)
(8)
k=0
远壁面采用方程如下:
(9)
(10)
(11)
其中取σε=1.3,cε1=1.41~1.45,cε2=1.9~1.92。
2.2 折流杆换热器边界条件设定
2.2.1 单独段内部边界条件设定
导流筒或折流栅入口采取速度边界条件,湍流强度采用水力直径和湍流强度进行衡量,其中湍流强度对于不同Re采用下式计算:
(12)
换热管内壁采用固壁温度,设定为373 K;流体与固体交界面采用耦合边界条件;流体出口采用压力出口边界条件,壳体外壁面采用自然对流边界条件,其对流传热系数设为10;管子出口设为绝热边界条件。
2.2.2 段与段之间连接边界条件设定
上下两段之间的连接采取上一段出口的速度、温度、湍动能、耗散和比耗散率与下一段折流栅入口相等,保证工艺参数的无缝连接,相互关系如下:
w上段出口=w下段入口v上段出口=v下段入口T上段出口=T下段入口k上段出口=k下段入口
ω上段出口=ω下段入口u上段出口=u下段入口ε上段出口=ε下段入口
3 求解结果分析
3.1 壳程流体流动与传热流场分析
图3为不同折流圈宽度折流栅温度云图,分别给出了当入口速度为0.5 m/s时,X(41)L(0)、X(41)L(2)、X(41)L(5)及X(41)L(10)折流栅第一段对称面温度云图。
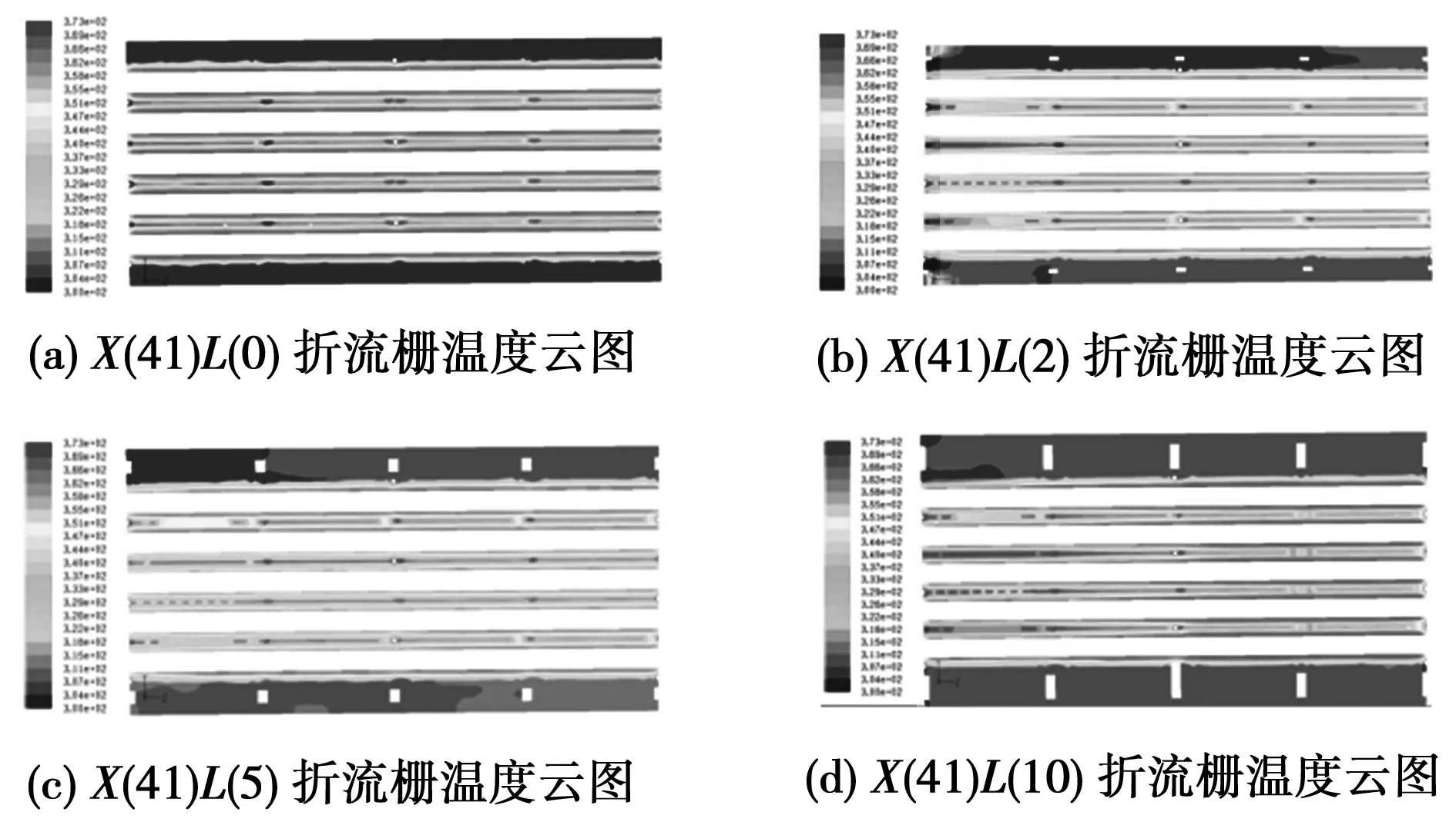
图3 折流栅温度云图
折流栅温度云图可以看出,随着折流圈宽度的增加,折流圈所在的旁流流路温度不断升高。图3(a)为没有折流圈的对称面云图,其壳体内径附近温度基本没有升高,图3(b)为折流圈宽度为2 mm,其左右两端及下方温度明显高于图3(a)的相同位置,可知由于折流圈的扰流使得折流圈附近的旁流流路参与传热。图3(c)和图3(d)其折流圈宽度分别增大,由图可以看出,其折流圈附近的高温区域面积逐渐增大。这是由于折流圈的扰流作用不断增强使得流体传热更加均匀。
图4为不同折流圈宽度折流栅速度云图,分别给出了当入口速度为0.5 m/s时,X(41)L(0)、X(41)L(2)、X(41)L(5)及X(41)L(10)折流栅第一段对称面速度云图。
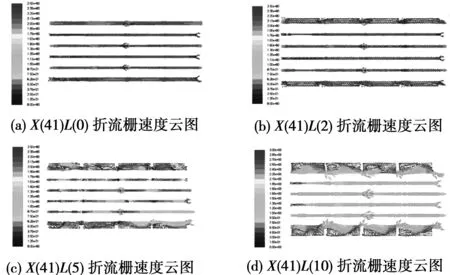
图4 折流栅速度云图
从速度云图的流体流动状态来看,随着折流圈的宽度不断增加,流体的混乱度在增加。图4(a)为无折流圈折流杆换热器,基本上为平行流动,只在折流杆附近非常小的范围内有一定的扰流。由此可见折流杆对流体的扰动影响比较小。从图4(b)可以看出,在折流圈尾部产生了扰流流动,但是影响范围仅在折流圈附近,绝大部分的旁流流路仍处于平行流。而随着折流圈的增加,如图4(c)可以看出,基本整个旁流流路的平行流都被打乱,形成半漩涡流动。当折流圈继续增加,从图4(d)可以看出,整个旁流流路不仅仅平行流全部消失,并且完全形成了旋涡流,而在折流杆附近的流体其扰流作用也有所增强。这说明了折流圈的扰流作用不仅仅强度要远远大于折流杆,并且影响范围也要远远大于折流杆。
从速度云图的流体速度分布可以看出,图4(a)流体流速基本处于平行流,其最大流速约为1 m/s左右,而随着折流圈宽度增加,流体流速不断增加。而在图4(d)中其最大流速发展到约为2.5 m/s左右。这说明折流圈的扰流作用,造成流体的分布极不均匀,从而可以在局部造成大雷诺数的漩涡流。
图5为不同折流圈宽度折流栅压力云图,分别给出了当入口速度为0.5 m/s时,X(41)L(0)、X(41)L(2)、X(41)L(5)及X(41)L(10)折流栅第一段对称面压力云图。
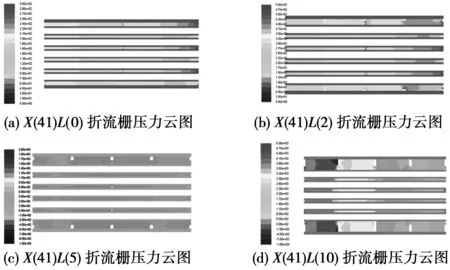
图5 折流栅压力云图
从压力云图的整体分布来看,随着折流圈的宽度增加,总的压降不断增加。如图5(a)当无折流圈时,其压降约为300 Pa左右。图5(a)其最大压降约为500 Pa左右,而图5(d)压降最大增加到6 000 Pa。说明了当折流圈的宽度较小时,对压降的影响和折流杆相差不大,而当折流圈宽度不断增加时,其对压降的影响要远大于折流杆的影响。从单张压力云图的内部分布来看,其压力分布呈现分块式分布,两个折流圈内部压力场基本均匀,而跨越折流圈后压力会发生跳跃式下降。这说明了折流杆换热器其压降损失主要是折流圈和折流杆导致的。而在图5(c)与图5(d)内部可以看出已经出现负压的情况,如图5(d)所示,其负压往往发生在折流圈背部,这说明了当折流圈宽度增加到一定范围时,其背部逐渐形成了旋涡。
3.2 壳程流体流动与传热数据分析
为了客观地衡量折流圈宽度对折流杆换热器壳程流动与传热的影响,对于不同壳径的折流杆换热器引入折流圈宽度与壳体内径之比ζ,其中ζ=L/(L+X)。图6为Nu-ζ、fe-ζ、Nu/fe-ζ关系图,分别给出了不同壳径下,随着ζ增大,努塞尔数Nu,阻力系数fe及综合系数Nu/fe的变化情况。
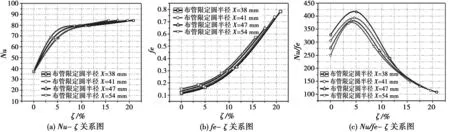
图6 Nu-ζ,fe-ζ,Nu/fe-ζ关系图
从图6(a)可以看出随着ζ增加,折流杆换热器Nu不断增大,说明折流圈的扰流对传热起到了强化作用;当ζ<7时,Nu随着ζ增加较明显,当ζ>7时,Nu随着ζ增加较慢,并逐渐趋于平缓。说明当折流圈增加到一定尺寸,其扰流作用对壳程传热影响逐渐减小。从不同布管限定圆X来看,Nu随着ζ的变化趋势一致,说明美国菲利普公式采用泄流面积与壳程面积比Al/As去衡量折流杆换热器壳程传热性能是正确的,也说明ζ是影响折流杆换热器壳程流动与传热的核心因素。在相同ζ时,布管限定圆X越大,其Nu略微增大。
从图6(b)可以看出随着ζ增加,阻力系数fe不断增大,说明折流圈的扰流在起到强化传热的同时也增加了阻力损失;并且随着ζ不断增加,其fe增加速度在加大。从不同布管限定圆X来看,fe随着ζ的变化趋势一致,在相同ζ时,布管限定圆X越大,其fe略微增大。
从图6(c)可以看出随着ζ增加,综合评定系数Nu/fe先增加后减小,当ζ在5%左右达到最大。当偏离峰值一定距离时,Nu/fe迅速减小。从不同布管限定圆X来看,Nu/fe随着ζ的变化趋势一致,但峰值位置略有偏差,最佳推荐值在4%-6%。在相同ζ时,布管限定圆X越大,其Nu/fe略微降低,这是由于当布管限定圆X较大时,其长径比减小导致折流杆换热器的效率会略微下降引起的。
表2为对X=38与X=54折流杆换热器壳程流动与传热影响比较,从而定量分析布管限定圆半径对折流杆换热器壳程Nu,fe及Nu/fe的影响。

表2 X对折流杆换热器壳程流动与传热影响
从表2可以看出X=54相对于X=38增量为42%,对于不同ζ时,其Nu平均增量约为3%,可认为X每增加10%,其Nu数约增加0.7%。其fe平均增量约为10%,可认为X每增加10%,其fe数约增加2.4%。其Nu/fe平均减量约为6.7%,可认为X每增加10%,其Nu/fe数约减少1.6%。
4 结 论
本文通过对折流杆换热器在不同折流圈宽度与壳体内径比下进行流动与传热分析,分析出对于不同布管限定圆半径X的折流杆换热器随着ζ的变化,其Nu,fe及Nu/fe的变化趋势基本一致。在相同ζ下,X每增加10%,其Nu增加0.7%,fe增加2.4%,Nu/fe减少1.6%。
注:X为布管限定圆半径/mm,L为折流圈宽度/mm,u,v,w为x,y,z方向速度m/s,T为温度/K,k为流体湍动能/J,ω为流体比耗散率,ε为耗散系数,I为流体湍流强度,ζ为折流圈宽度与壳体内径之比,Cp为定压比热容/J/(kg·K),λ为导热系数/W/(m·K),ρ为流体密度/kg/m,μ为流体动力粘度/N·s/,Nu为努塞尔数,fe为阻力系数。
