基于EXCEL的企业投资决策动态模型设计
2019-12-12马悦

摘 要:在市场经济下,企业能否将筹集的有限资金投放到收益高、风险低、回报快的项目中,对企业的生存和发展十分关键。本文通过案例方式介绍如何利用Excel,对项目投资决策中固定资产更新决策及多个项目的投资决策进行模型设计与应用。
关键词:Excel;项目决策;固定资产更新;多个项目决策
一、固定资产投资决策分析
在企业经营发展过程中,考虑到旧设备生产效率及耗费性能,时常面临着固定资产更替的情况,在进行决策分析时,需要考虑企业是否购置新设备,还是继续使用现有旧设备。
本文重点研究基于Excel分析投资项目产生的现金流,从而计算项目决策指标,设计固定资产更新决策模型。利用Excel的函数功能,进行固定资产项目更新换代的财务决策。
【案例1】大福公司现有一台旧机床是三年前购进的,旧设备原值为84000元,税法规定残值为4000元,最终报废残值为5500元。税法规定使用年限为8年,已使用三年,目前变现价值为40000元,尚可使用年限为6年。旧设备在投资项目建设初期需要垫支营运资本10000元,每年的营运成本为13000元,按折现法计提折旧,每年折旧费10000元。若继续使用旧设备,将于继续使用的第二年年末支付18000元大修理支出;现有一台新机床可供选择,新设备原价为76500元,税法规定残值为4500元,最终报废残值为6000元。税法规定使用年限为6年,营运资金垫支为11000元,第四年末支付9000元大修理费用。每年按直线法计提折旧12000元,年营运成本7000元。公司所得税税率为40%,资本成本率为10%。该企业考虑是否购入一台新机器设备来替代现有旧设备,提高公司生产效益,实现企业价值最大化。通过具体案例来阐述利用Excel进行固定资产更新决策建模。
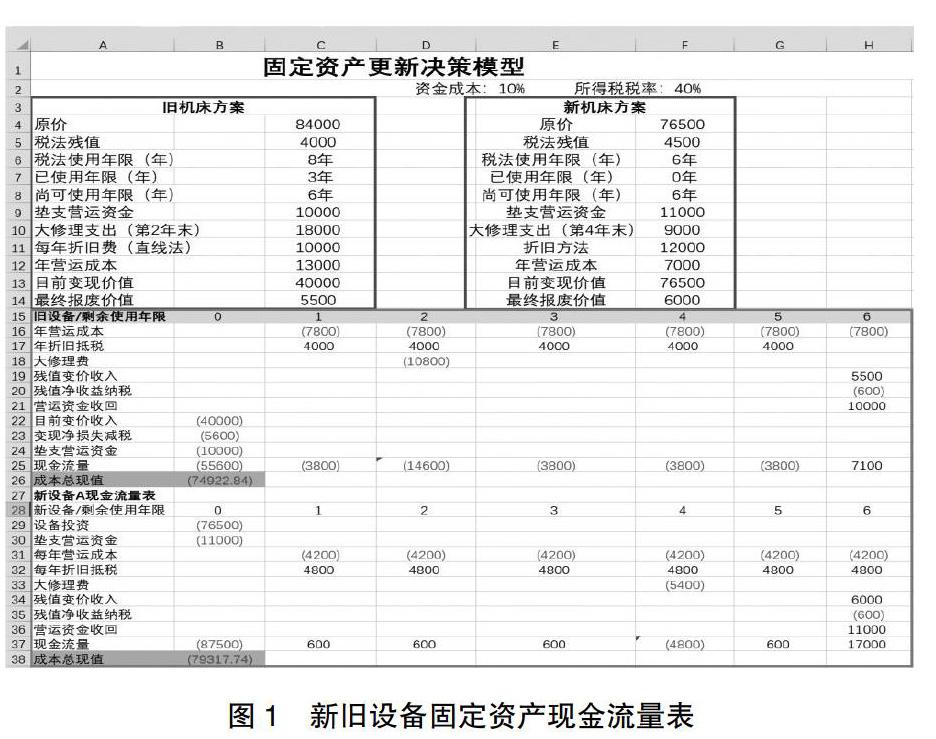
利用Excel建立新旧设备固定资产现金流量表(图1)。在新旧设备寿命期相同时,默认更新不改变生产能力,即新旧设备销售收入相同,属于非相关流量。故决策时应选择现金流出总现值较低者。
第一步,按照直线折旧法对旧设备进行计提折旧。在单元格C11,录入公式SLN(C4,C5,C6)。第二步,计算营业阶段现金流。在单元格C16中,输入税后年营运成本计算公式=-C12*(1-40%),复制该公式,粘贴至单元格D16至H16中;在单元格C17中,录入年折旧抵税计算公式=C11*40%,复制公式粘贴至单元格D17至G17中;在单元格D18中,录入税后大修理费用=-C10*(1-40%);第三步,计算终结阶段现金流。在单元格H19中,录入终结时点残值变价收入5500;在单元格H20中,录入残值净收益纳税公式=-(C14-C15)*40%;在单元格H21中,录入收回在初始阶段垫支的营运资金10000。第四步,计算初始阶段现金流。在单元格B22中,录入目前变价收入-C13。在单元格B23中,录入变现净损失减税=-(C4-C11*C7-C13)*40%;在单元格B24中,录入项目在投产前垫支的营运资金-10000。第五步,利用Excel中净现值(NPV)函数进行计算分析。选中单元格B26,录入公式=NPV(10%,C25:H25)+B25,计算得出旧设备的成本总现值为74923元。选中新设备单元格B38,输入净现值公式= NPV(10%,C37:H37)+B37,计算出新设备的成本总现值为79318元。
在两方案营业收入一致的情况下,新设备现金流出总现值为79318元,旧设备现金流出总现值为74923元。因此,继续使用旧设备比较经济。
二、多个项目的投资决策模型设计与案例分析
企业财务人员在进行投资项目有效性分析时,还需要考虑项目之间的相互关系,例如,当项目之间存在互斥关系时,在资源限制的情况下两个项目不能同时共存;当项目间存在预备关系时,一个相关项目上马,另一个项目必须上马。本文借助Excel进行0-1规划模型,可以数量化地解决项目间存在的开与关、取与弃、有与无等反映出的离散变量间的逻辑关系、顺序关系以及互斥的约束条件。
【案例2】南京腾飞是一家新能源汽车股份公司,为了进一步实现企业价值最大化的财务目标,公司董事会决议针对今后两年2020年-2021年进行投资规划部署。资产管理部、投资管理部、战略发展部的多重评估,现有6个项目可供公司财务部门进行经济有效性分析。已知6个备选方案的投资期均为两期,且投资项目的资本限额分别为1000万和400万。相关数据如表所示。
現由于市场关系限制,6个备选项目存在如下关系:项目1、项目2、项目3为多择一项目,三个项目中有且只有一个被选中;项目2是项目4的预备项目,项目5与项目6为互斥项目。
1.多个项目投资决策的数学模型设计
第一步,设计变量。令
2.多个项目投资决策的Excel模型设计与应用
第一步,根据上述数学模型,运用Excel规划求解工具,设计相关模型,得出最优解。在Excel菜单栏中点击“文件”,选择“选项”,点击“自定义功能区”,选中“自定义功能区”下的主选项卡“开发工具”;在菜单栏中点击加载出的“开发工具”,点击“加载项”,选中其中的可用加载宏“规划求解加载项”;选中菜单栏中“数据”,点击手动加载出的“规划求解”。在Excel中建立基础数据区,输入已知数据,如下图2。
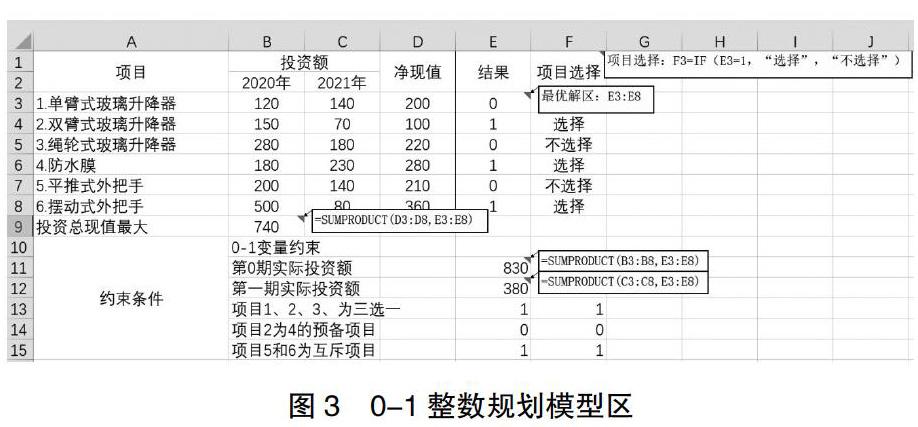
第二步,建立0-1整数规划模型区,如下图3。选定可变单元格E3:E8,在表中输入任意初始值,假定均为0;根据单元格E3:E8的结果,输入IF函数语句,F3=IF(E3=1,“选择”,“不选择”);确定目标单元格B9,定义为目标函数值,表示投资总的最大净现值,输入目标函数=SUMPRODUCT(D3:D8,E3:E8),表明投资总现值最大值为D3*E3+D4*E4+D5*E5+D6*E6+D7*E7+D8*E8;输入约束条件,选定单元区E11:E15。利用SUMPRODUCT函数,依次输入E11= =SUMPRODUCT(B3:B8,E3:E8),E12= =SUMPRODUCT(C3:C8,E3:E8)。
第三步,设置规划求解参数。选中菜单页面下“数据”,选定“规划求解”。设置目标为$B$9,选定“最大值”。确定可改变区域$E$3:$E$8。依次输入约束条件,$E$11<=$F$11、$E$12<=$F$12、$E$13=$F$13、$E$14<=$F$14、$E$15<=$F$15、$E$3: $E$8=二进制,约束值为“int”整数。
第四步,应用Excel规划求解工具“求解”,得到结果图4,选择项目2、项目4、项目6时,解出最优解投资总现值最大值为740万元。
财务人员可以利用EXCEL对财务决策项目进行建模分析,克服传统手工条件下建模及计算正确率不高、效率低下的问题。能够帮助财务人员及时、正确、有效地计算及评价投资项目的经济有效性。
参考文献:
[1]陆翠丽.EXCEL在长期投资决策中的应用[J].时代金融,2018(36):412-413.
[2]郁玉环.Excel“规划求解”在多方案组合排队投资决策中的应用[J].中国管理信息化,2009,12(04):28-30.
作者简介:马悦(1993.01- ),女,籍贯:盐城市,南京审计大学金审学院,助教,硕士研究生,研究方向:企业并购
