考虑负载扰动的电液转向系统控制研究
2019-12-12
(1.太原科技大学重型机械教育部工程研究中心,山西太原 030024;2.太原工业学院机械工程系,山西太原 030024; 3.宁波中意液压马达有限公司,浙江宁波 315000)
引言
目前,全液压转向器广泛地应用在农机转向系统上,转向器的转向精度直接影响车辆的行驶轨迹,然而由于内泄漏的原因导致全液压转向器控制精度较低。随着“精细农业”的提出和智能化、自动化发展的趋势,电液伺服系统以其较高的控制精度和较高的自动化水平的优势,逐渐地被用在转向系统中。
电液伺服转向系统是农机自动导航控制系统的重要组成部分。转向油缸克服转向力后推动转向轮实现转向,然而电液伺服系统本身具有非线性,转向力也是未知的,不同的路面、轮胎、载荷其转向力不同,变化过程非常复杂,严重影响伺服系统的性能。许多学者对此类系统提出控制方案。吴晓明、顾凯等[1-2]针对电液伺服系统中的摩擦力,在深入分析和大量试验的基础上,设计了摩擦力观测器,提出了摩擦力补偿方法。针对转向系统非线性采用模糊PID控制策略,实现了良好的定位精度和较高的动态特性,然而模糊控制需要做专家数据库,实际应用较难达到满意效果[3-4]。文献[5]采用自适应控制策略抑制伺服系统参数变化带来的影响,使系统具有很强的鲁棒性。党选举等[6-8]针对电液伺服系统的强非线性特性设计了滑模控制器,达到了很好的跟踪精度。然而不可避免产生抖振现象。石胜利等[9-12]针对电液伺服系统设计了反演控制算法,仿真结果表明反演控制算法响应快,鲁棒性强,然而反演控制算法计算量大,工程上难以实现。
本研究先借助负载观测器,在线估计电液转向系统的负载力,然后用二次性能指标对电液转向系统进行最优控制,最后用观测到的负载力对系统前馈补偿,提高了系统跟踪精度,增强了抗转向力扰动性能。
1 电液转向系统原理及数学模型
本研究所研究的电液转向系统原理图如图1所示。系统由油泵、溢流阀、全液压转向器、高频响比例阀、转向油缸组成。电液转向系统工作时比例阀控制转向油缸动作,全液压转向器在此作为冗余备份,系统正常运行时全液压转向器并不动作,可见,电液转向系统本质是一个四边滑阀控制对称油缸系统,其示意图如图2所示。

图1 电液转向系统原理图

图2 电液转向系统示意图
电液转向系统采用的传感器和比例阀功率放大电路的固有频率远远高于液压系统固有频率,把两者视为放大环节,即:
i=Kapu
(1)
uf=KfxL
(2)
式中,i为比例阀线圈的电流;u为输入放大器的电压信号;uf为传感器的输出电压信号;xL为转向油缸的位移。
比例阀的流量压力方程:
q=KqxV-KcpL
(3)
式中,Kq=KaKsq,Ka为比例电磁铁增益;Ksq为阀口的流量增益;Kc为阀口的流量压力系数;xV为比例阀的阀芯位移;pL为转向油缸两腔的压力差。
转向油缸的力平衡方程:
(4)
式中,m为电液转向系统运动部件折算到转向油缸的质量;Ap为转向油缸有效面积;Bp为黏性阻尼系数;K为负载刚度;FL为负载力。
流量连续性方程:
(5)
式中,βe为油液弹性模量;vt为转向油缸容腔体积;ctp为油缸总泄漏系数。
选取状态变量:
则电液转向系统模型写成状态空间方程形式为:

(6)
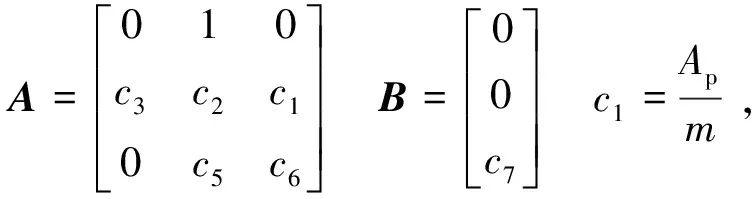

2 基于负载力观测器的前馈最优状态反馈控制策略


图3 电液转向系统前馈二次型最优控制方框图
2.1 转向力的观测
电液伺服系统负载的特性直接决定了系统的动态性能。对电液转向系统来说,负载的质量一般是固定的,并且比较容易获得,然而负载力却随着不同的路况变化。由于转向力难以测量,本研究设计观测器精确地估计系统的转向力,以便于补偿转向力导致的位置误差。
目前对负载力的观测方法主要有Luenberger观测器、扩展kalman滤波器和滑模观测器。扩展kalman滤波器有较好的抗干扰能力,但是其算法较为复杂,滑模观测器虽然具有较好的抗干扰能力,但是存在抖动问题,不利于工程应用。Luenberger观测器通过系统的输出和输入实现对系统的观测,其在干扰不大的系统中收敛迅速。本研究采用如下的Luenberger观测器:

(7)
其中状态变量:

Luenberger观测器的系数可以通过极点配置法[13]确定。由式(7)得系统方程特征根为:
det(sI-A-LC)=0
(8)
假设观测系统的极点期望位置为β1,β2,β3和β4,则系统的特征方程为:
(s-β1)(s-β2)(s-β3)(s-β4)=0
(9)
比较和的系数,可得:
L1=c2-β1-β2-β3-β4+c6
(10)
L2=c3+L1·c2+L1·c6+β1·β2+c1·c5-c2·c3+
β4·(β1+β2+β3)+β3·(β1+β2)
(11)
L3={L2·c6-L4·c4-c3·c6-β4·[β1·β2+
β3·(β1+β2)]+L1·c1·c5-L1·c2·c3-
β1·β2·β3}/c1
(12)
L4=-β1·β2·β3·β4/(c4·c6)
(13)
2.2 最优状态反馈控制设计
对于电液转向系统(6),根据二次型最优控制理论,最优控制的目的就是找到一个最优控制输入U,使的系统的误差e和所需的控制量最小,用二次型性能指标函数表示为:
(14)
式中,Q,R为权矩阵;Q为半正定对称阵;R为正定对称阵。
通过求解Riccati方程:
PA+ATP-PBR-1BTP+CTQC=0
(15)
得到实对称矩阵P,从而得到最优反馈增益矩阵:
K=R-1BTP=[K1K2K3]
(16)
3 仿真研究
借助于MATLAB/Simulink工具对所设计的控制策略仿真,仿真参数如表1所示。

表1 主要仿真参数
式(6)中矩阵系数计算如下:
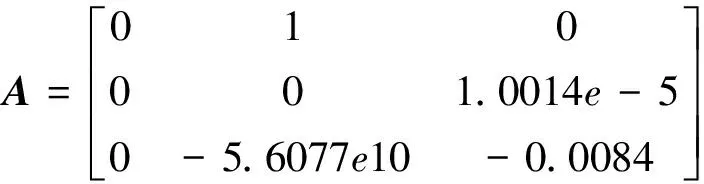
取R=1,Q=diag(20 1e-8 1e-11),借助MATLAB工具解Riccati方程求出反馈增益:
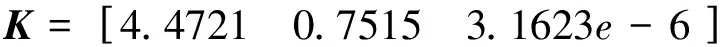
观测器系数为:
L[-3.4552e3 2.3222e7-7.0660e15
-7.6275e8]T
电液转向系统的仿真框图如图4所示。首先对比了PID控制算法与LQR控制算法的跟踪性能。给定位移参考值为xd=0.2×sin(πt)。 图5为转向负载力为0时,系统的位移跟踪曲线和给定位移参考曲线,图6为对应的误差曲线,可以看出LQR算法的跟踪性能较好。 图7为LQR控制算法控制的系统跟踪误差曲线,当系统不加转向负载力时,系统的最大跟踪误差为0.8 mm。当系统加入转向负载力FL=5000×sin(1.5πt),跟踪曲线出现较大的偏差,最大跟踪误差达到2.3 mm。为了消除转向负载力的影响,提高系统刚度,加入负载前馈补偿策略。转向负载力由负载观测器获得,图8为转向负载力的给定值曲线和观测器估计值曲线,可见观测器的跟随性能良好。图7可知加入负载力前馈补偿策略后,最大跟踪误差降低为1 mm,接近不加转向负载力时的误差,这说明前馈补偿策略有效地降低转向负载力对系统的影响。图9为负载观测器对阶跃负载力的估计,图8和图9可看出所设计的观测器可以比较准确、快速地估计出实际负载力。

图4 电液转向系统仿真框图
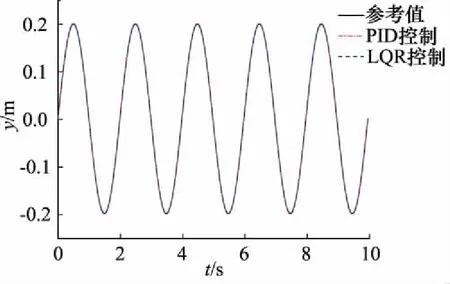
图5 位移跟踪

图6 PID控制与LQR控制误差
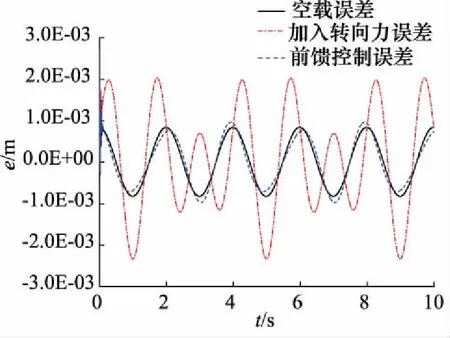
图7 LQR控制跟踪误差

图8 正弦转向负载力估计

图9 阶跃转向负载力估计
4 实验研究
为了进一步验证本研究中的控制策略,按照图1所示的液压系统原理图,基于某型号拖拉机液压转向系统搭建测试平台,其主要组成部分包括车辆转向系统、电液比例阀、溢流阀、阀块、传感器、放大器和控制器。转向系统包括全液压转向器、转向油缸。电液比例阀和溢流阀安装固定在阀块上,转向油缸用液压软管与阀块连接在一起。由于车辆的内部空间所限,采用转角传感器间接地测量转向油缸的位移值,传感器安装方式如图10所示。图11是控制原理图。控制算法运行在微控制器中。指令信号和传感器信号经过模拟量接口进入控制器,微控制器处理输入的信号,通过模拟量输出接口输出给放大器,放大器驱动比例阀电磁铁进行相应的动作。

图10 传感器安装方式

图11 控制原理图
空载试验时,用千斤顶把车辆转向轴略微抬起,保证轮胎不接触地面;加载试验时,去掉千斤顶,车辆原地静止,轮胎在原地转向。
为了测试系统的跟踪性能,给定的参考位移信号为平滑处理过的阶跃信号(图12)。位移跟踪测试结果如图13所示。首先采用本研究中的最优反馈控制策略,为了测试系统的空载跟踪性能,测试时转向轮轮胎不接触地面。图14为位移跟踪误差曲线,可知此时系统最大跟踪误差为3.5 mm。然后测试带有转向负载力的跟踪性能。由于负载力的影响,此时最大跟踪误差增大为4.4 mm。最后,在最优反馈控制策略上加入负载观测器,得到转向力估计值如图15所示。在此基础上把估计得到的转向力前馈补偿到系统的输入,再次测试其跟踪性能。由于负载干扰得到补偿,系统最大跟踪误差降低为3.7 mm。图14中,随着转向油缸位移变大,轮胎产生弹性变形,观测到的转向力也逐渐变大。在转向油缸位移稳定后,仍能观测到较大的负载力,这是由于试验时轮胎在原地转向,轮胎与地面有较大的摩擦力,且转向油缸位移稳定后轮胎弹性变形仍然存在,因此负载力仍然存在。

图12 给定位移信号曲线
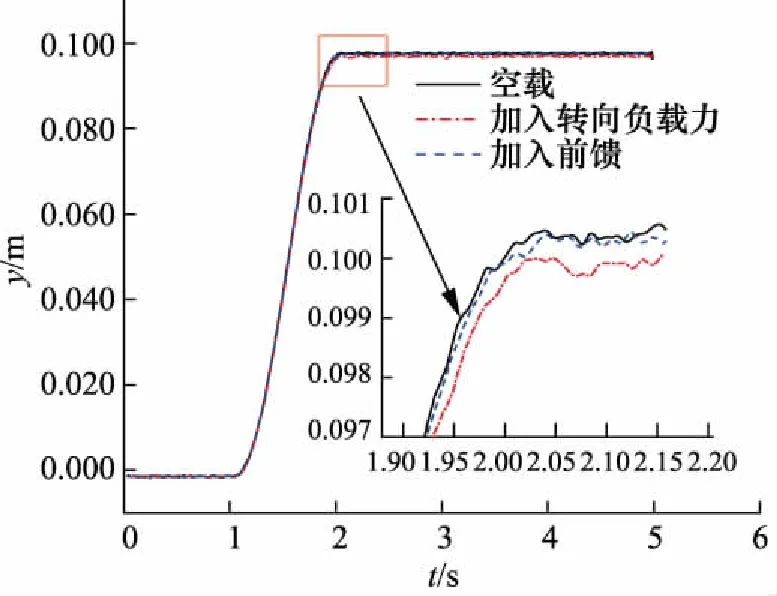
图13 位移跟踪曲线

图14 误差曲线

图15 转向负载力估计曲线
对比图13中的3条曲线可知,基于观测器的前馈和最优状态反馈复合控制策略具有较高的跟踪精度和抗负载干扰能力。
5 结论
针对电液伺服转向系统易受到转向力干扰的问题,建立了转向系统的动态模型,提出了基于观测器前馈补偿的最优状态反馈控制策略,仿真和试验结果表明,该控制策略可以有效地减少由转向力引起的转向误差,抑制转向力的干扰,提高电液转向系统的控制精度。
