电液力伺服系统自适应抗扰控制研究

李 波1，芮光超1, 方 磊1, 撒韫洁, 汤 裕, 沈 刚

(1.中国船舶重工集团公司第七一三研究所，河南郑州 450000； 2.中国矿业大学机电学院，江苏徐州 221116)

引言

电液伺服系统由于具有功率质量比高、负载刚度大、有效载荷能力强、响应速度快等特点。被普遍应用在航空航天、武器装备、能源冶金、海洋设备、矿山机械等方面[1]。由于电液伺服阀存在流压特性及其控制体积的变化等因素，导致电液伺服系统的动态行为具有高度非线性，同时因为模型的不确定性尤其是存在参数不确定性，给控制系统带来了困难[2]。

为提高电液伺服系统控制性能，不仅需要提高伺服系统的精度，同时还需要对外界存在的干扰进行抑制，许多研究人员已经在控制研究中引入了非线性控制策略，如反演控制、反馈线性化、滑模控制以及神经网络控制等，并取得了较好的控制效果。符晓玲等[3]利用状态反馈线性化的方式对IPMSM模型进行了精准的线性化建模和动态解耦；张扬等[4]设计了一种反演控制器用以控制状态受限的非线性系统；严乐阳等[5]设计了一种基于MLVSC算法的控制策略来提高控制精度；董振乐等[6]构造了一种基于自适应鲁棒控制的预设性能追踪控制方法；赵贺伟等[7]使用动态神经网络算法控制高超声速飞行器的动力学模型。

近年来，基于反步法的控制研究及应用得到了国内外学者的注重，反步控制是一种较新的、应用较广泛的针对非线性系统的控制策略。传统的反步控制法所设计的控制器虽然能确保系统的全局稳定性[8]，却较少的考虑系统参数摄动和外界干扰对系统的影响，导致控制器的鲁棒性较弱。而滑动模态变结构控制对负载扰动及参数摄动并不敏感，是一种强鲁棒性的控制策略。

滑模控制是一种应用较广的非线性控制方法，其基本方法为通过定义一个滑模面，使得系统趋向滑模面运动[9]。而在运动至滑模面的过程中，常见的趋近律有等速、指数、幂次等[10-11]。针对滑模控制中存在的抖动，近年来也有许多研究者提出了如动态滑模、智能控制等弱化的方法。由于滑模的实现方法简单，也与越来越多的其他控制方法相结合，如滑模观测器，滑模鲁棒控制，反步滑模[12]等方法，有效的提高了原来系统的鲁棒性，降低了对外界干扰的敏感程度。

在力控制的非线性方程建立过程中，因为没有考虑外界的未知干扰以及建模过程中物理参数的变化，模型的准确性会受到影响，所以通过自适应的方法让这些参数实时的变化，能更好的控制液压缸的动作。同时，通过利用滑模的方法抵偿外界的一些未知情况，从而提高系统的鲁棒性。在建立状态方程后，设计控制器的过程中首先针对参数的变化设计了参数自适应率，然后对于外界未知上限的干扰利用估计值来进行补偿，最后在反步控制器的第三步推导中引入滑模面，来降低系统对干扰的敏感性。

综上所述，当存在较大的外界干扰时，电液系统的精度及稳定性下降明显，本研究提出一种基于反步法与滑模控制结合的自适应鲁棒控制策略，利用2个液压缸来分别模拟力控制和外界干扰，最终实现干扰抑制。

1 电液力伺服系统的非线性数学模型

如图1所示为液压动力机构模型，该动力机构采用阀控对称油缸的形式。首先假设是1个零开口滑阀，其供油压力ps恒定，且回油压p0是0，并合理忽略

图1 液压动力机构简图

系统的压缩流量、流体质量和摩擦。

以此假设建立三位四通阀的流量连续性方程、液压缸的流量连续性方程和系统的力平衡方程：

(1)

式中,QL1为阀的流量；Kq为阀的流量增益；Kc为阀的流量压力系数；pL为负载压降,pL=p1-p2；QL2为液压缸的流量；Ap为液压缸活塞有效面积；xp为活塞位移；Ctp为液压缸内泄漏系数；Vt为液压缸两腔总容积；βe为有效体积弹性模量；M为活塞及负载折合到活塞上的总质量；Bp为活塞及负载的黏性阻尼系数；FL为作用在负载上的任意外负载力。

为了采用引入滑模控制的反步法控制电液系统，首先需要将电液系统改写为系统状态方程，且系统的非线性方程需写成反步法所需的严格反馈形式，状态变量的定义如下：第一个状态量为力，第二个为力加载缸的速度，第三个为液压缸左右腔的压差：

(2)

考虑系统的建模误差以及外界干扰等因素，系统状态方程可改写如下，其中Δ为总干扰：

(3)

状态方程系数如下：

(4)

2 控制器设计

在对设计系统的反步控制器的过程中，首先定义误差信号ef1,ef2,ef3,并引入虚拟控制量αf1,αf2,其中x1r为给定力参考信号：

ef1=xf1-x1r，ef2=xf2-αf1，ef3=xf3-αf2

(5)

2.1 设计步骤1

为了使跟踪误差ef1趋近于0，定义一个半正定的Lyapunov函数:

(6)

由上述的状态方程可知:

(7)

对方程式(6)两侧求导，并将系统的状态方程代入：

(8)

可使虚拟控制量为：

(9)

其中，k1f为大于0的正数，代入式(8)得：

(10)

2.2 设计步骤2

定义一个半正定的Lyapunov函数为：

(12)

同时：

(13)

对函数两侧求导，并将系统的状态方程代入：

(14)

可使虚拟控制量为：

(15)

其中k2f为大于0的正数。所以:

(16)

为了第三步计算的需要，将α2进行求导并进行化简：

(17)

(18)

2.3 设计步骤3

在最后一步的推导中，为了消除外界的干扰，使得控制器具有更好的鲁棒性，引入滑模面。同时考虑到参数的不确定性，定义参数误差为：

s=c1ef1+c2ef2+ef3

其中,c1,c2为正常数。对滑模函数求导得：

(19)

综合考虑了参数的自适应和干扰的自适应情况，定义一个半正定的Lyapunov函数为:

(20)

对函数两侧进行求导，并将系统的状态方程和滑模函数代入,可以求出最后的输入流量和自适应率如下：

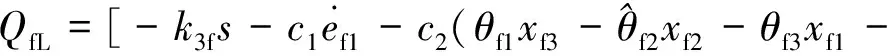
(21)

(22)

将式(21)和(22)代入公式(20)得：

(23)

为了使最后的V函数能够小于0，需要进一步的设计和要求，将公式改写如下：

=-ETQE-k3fs2

(24)

其中：

E=[ef1,ef2,ef3]T

(25)

采用这种设计的原因是，如果Q是正定矩阵，那么根据正定矩阵的等价命题，当某一个实对称矩阵为正定时，其所有顺序主子式均为正等价于该矩阵为正定矩阵。为了确保系统是渐进稳定的，求出矩阵Q的顺序主子式并且令其均大于0，那么设计的自适应反步滑模控制器的参数应满足如下条件：

(27)

控制器的设计方案如图2所示

图2 系统控制原理图

通过提出的自适应鲁棒控制器可以发现，在引入了自适应、滑模和干扰估计值的方法来进行控制器信号补偿后，可以进一步降低位置干扰对耦合系统下的力加载信号的影响。

3 实验验证

3.1 试验台

如图3所示，实验验证过程中使用的电液力伺服系统试验台主要由振动台、对称液压缸、电液伺服阀、油源以及连接铰等组成。振动台可用于安装被试件或设备，并通过铰接连接至液压缸，伺服阀和液压缸通过将液压源提供的液压能转化为机械能，为平台提供运动动力，试验台主要参数如表1所示。

图3 电液力伺服系统试验台

表1 试验台主要参数

图4是试验台控制系统原理示意图，指令信号通过控制算法产生所需要的力信号，并与振动台的输出力信号形成力闭环；控制器将输出-10～+10 V的驱动信号，并由D/A板卡ACL-6126发送，产生驱动信号再经由信号调理电路和功率放大器产生-40～+40 mA的电流信号，用以对电液伺服阀的运动进行驱动。电液伺服阀根据所需的驱动信号控制进入液压缸的液压油，从而使振动台按照期望的运动进行动作。

图4 试验台控制原理示意图

3.2 实验结果

试验过程中，首先将试验振动台运动到中间位置，随后输入频率2～15 Hz，幅值5000 N的随机力加载信号，并在另一端由位置系统施加随机位置干扰信号。首先进行单独的PID力控制实验，获得如图5所示的跟踪曲线，然后，切换到反步控制器，得到的跟踪曲线如图6所示，最后使用自适应反步滑模控制器进行实验，得到如图7所示的跟踪曲线。

根据三张图的横向对比可以看出，外界干扰对系统的跟踪性能存在一定的影响，波形在某些区域已经出现了严重的失真。对比图5与图6、图7，可以看出，若存在外界的干扰，此时PID控制器的性能不如非线性控制器，给定的参考信号与实际反馈的值存在着一定的幅值相位差。再对比图6与图7，可以发现，在这两个非线性控制器之中，相比于简单的单一反步控制，自适应反步滑模的控制效果略有提高，即自适应的参数、估计干扰力以及设计的滑模面对系统性能的提升具有一定效果。

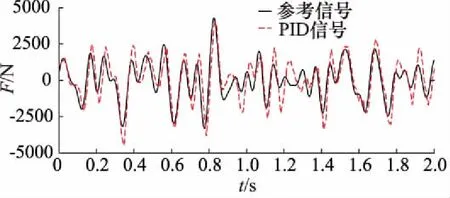
图5 有干扰下PID控制器跟踪曲线

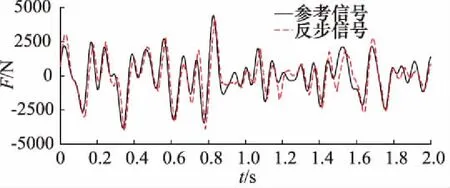
图6 有干扰下反步控制器跟踪曲线

图7 有干扰下自适应鲁棒控制器跟踪曲线

通过定性分析可以看出，由于提出的反步控制器在设计中考虑了多变量的输入输出，在控制上考虑了更多的误差信号，使控制精度更高。对比反步控制器和自适应鲁棒控制器，可以看出干扰又进一步的被抑制，证明引入的滑模面在一定程度上提高系统的鲁棒性和抗干扰能力。

为进一步对3种控制器的作用效果进行比较，对实验数据进行定量分析，得到3种控制器的跟踪信号与参考信号差值曲线如图9所示。并利用归一化均方根误差对实验数据进行比较，计算结果如表2所示，归一化均方根误差值越小，说明跟踪信号同参考信号之间的整体偏差越小。

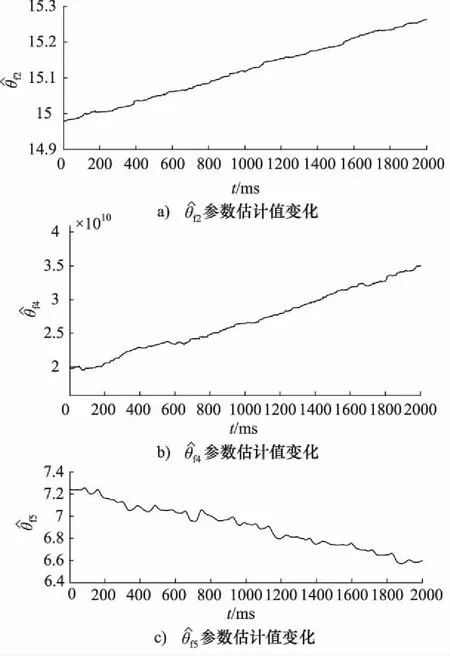
图8 力加载系统不确定参数估计值自适应曲线图

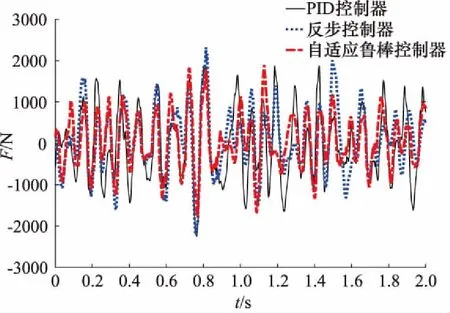
图9 各控制器跟踪信号与参考信号差值

表2 不同控制器力加载信号的归一化均方误差

由于评价控制策略性能的指标是一段时间内跟踪信号对参考信号的跟踪表达的准确性，由表2可知自适应鲁棒控制器归一化均方根误差值小于反步控制器和PID控制器，结合图5～图7的曲线可知，自适应鲁棒控制器的跟踪信号整体偏差较小，说明结合了自适应和滑模控制的控制策略，可有效改善控制器性能。

4 结论

针对电液力伺服系统存在的外界干扰，提出一种自适应的鲁棒控制器，在所设计的反步控制器基础上，增加了自适应滑模控制思想，并通过实验证实了控制策略的性能。实验结果表明，所提出的控制策略可以进一步提高电液力伺服系统的加载力的跟踪精度，具有良好的控制性能，对系统模型参数和外界带来的干扰得到了有效的抑制，所以该控制策略是切实有效可行的。